Rezultatele învățării

  • Determinați dacă datele sau un scenariu descriu o creștere liniară sau geometrică
  • Identificați rate de creștere, valori inițiale sau valori punctuale exprimate verbal, grafic, sau numeric, și să le transpună într-un format utilizabil în calcul

    • Calculează ecuații recursive și explicite pentru creșterea liniară și geometrică, având în vedere suficiente informații, și utilizează aceste ecuații pentru a face predicții

Având o rată constantă de schimbare este caracteristica definitorie a creșterii liniare. Reprezentarea grafică a perechilor de coordonate asociate cu o schimbare constantă va avea ca rezultat o linie dreaptă, forma creșterii liniare. În această secțiune, vom formaliza o modalitate de a descrie creșterea liniară folosind termeni și concepte matematice. La sfârșitul acestei secțiuni, veți fi capabili să scrieți atât o ecuație recursivă, cât și una explicită pentru creșterea liniară, date fiind condițiile inițiale sau o constantă de schimbare. De asemenea, veți fi capabili să recunoașteți diferența dintre creșterea liniară și cea geometrică, având în vedere un grafic sau o ecuație.

Creștere liniară (algebrică)

Predicând creșterea

Marco este un colecționar de sticle de suc vechi. Colecția sa conține în prezent 437 de sticle. În fiecare an, el bugetează suficienți bani pentru a cumpăra 32 de sticle noi. Putem determina câte sticle va avea peste 5 ani și cât timp îi va lua colecției sale să ajungă la 1000 de sticle?

În timp ce, probabil, ați putea rezolva ambele întrebări fără o ecuație sau matematică formală, vom formaliza abordarea acestei probleme pentru a oferi un mijloc de a răspunde la întrebări mai complicate.

Să presupunem că Pn reprezintă numărul, sau populația, de sticle pe care Marco le are după n ani. Deci P0 ar reprezenta numărul de sticle de acum, P1 ar reprezenta numărul de sticle după 1 an, P2 ar reprezenta numărul de sticle după 2 ani, și așa mai departe. Am putea descrie modul în care colecția de sticle a lui Marco se schimbă folosind:

P0 = 437

Pn = Pn-1 + 32

Aceasta se numește o relație recursivă. O relație recursivă este o formulă care leagă următoarea valoare dintr-o secvență de valorile anterioare. Aici, numărul de sticle din anul n poate fi găsit prin adăugarea a 32 la numărul de sticle din anul precedent, Pn-1. Folosind această relație, am putea calcula:

P1 = P0 + 32 = 437 + 32 = 469

P2 = P1 + 32 = 469 + 32 = 501

P3 = P2 + 32 = 501 + 32 = 533

P4 = P3 + 32 = 533 + 32 = 565

P5 = P4 + 32 = 565 + 32 = 597

Am răspuns la întrebarea câte sticle va avea Marco peste 5 ani.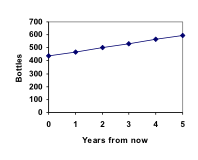

Cu toate acestea, rezolvarea problemei cât timp îi va lua colecției sale să ajungă la 1000 de sticle ar necesita mult mai multe calcule.

În timp ce relațiile recursive sunt excelente pentru a descrie simplu și curat modul în care se schimbă o cantitate, ele nu sunt convenabile pentru a face predicții sau pentru a rezolva probleme care se întind mult în viitor. Pentru aceasta, este preferabilă o formă închisă sau explicită pentru relația respectivă. O ecuație explicită ne permite să calculăm Pn direct, fără a fi nevoie să cunoaștem Pn-1. Deși este posibil să fiți deja în măsură să ghiciți ecuația explicită, haideți să o derivăm din formula recursivă. Putem face acest lucru prin nesimplificarea selectivă pe parcurs:

P1 = 437 + 32 = 437 + 1(32)

P2 = P1 + 32 = 437 + 32 + 32 = 437 + 2(32)

P3 = P2 + 32 = (437 + 2(32)) + 32 = 437 + 3(32)

P4 = P3 + 32 = (437 + 3(32)) + 32 = 437 + 4(32)

Probabil că acum puteți vedea tiparul și să generalizați că

Pn = 437 + n(32) = 437 + 32n

Utilizând această ecuație, putem calcula câte sticle va avea după 5 ani:

P5 = 437 + 32(5) = 437 + 160 = 597

Acum putem, de asemenea, să rezolvăm când colecția va ajunge la 1000 de sticle, înlocuind Pn cu 1000 și rezolvând n

1000 = 437 + 32n

563 = 32n

n = 563/32 = 17.59

Atunci Marco va ajunge la 1000 de sticle în 18 ani.

Etapele de determinare a formulei și de rezolvare a problemei colecției de sticle a lui Marco sunt explicate în detaliu în următoarele videoclipuri.

În acest exemplu, colecția lui Marco a crescut cu același număr de sticle în fiecare an. Această schimbare constantă este caracteristica definitorie a creșterii liniare. Reprezentând grafic valorile pe care le-am calculat pentru colecția lui Marco, putem observa că valorile formează o linie dreaptă, forma creșterii liniare.

Creștere liniară

Dacă o cantitate începe de la mărimea P0 și crește cu d în fiecare perioadă de timp, atunci cantitatea după n perioade de timp poate fi determinată folosind oricare dintre aceste relații:

Forma recurentă

Pn = Pn-1 + d

Forma explicită

Pn = P0 + d n

În această ecuație, d reprezintă diferența comună – cantitatea pe care populația o schimbă de fiecare dată când n crește cu 1.

Conexiune cu învățarea anterioară: Panta și intercepția

Puteți recunoaște diferența comună, d, în ecuația noastră liniară ca pantă. De fapt, întreaga ecuație explicită ar trebui să vă pară familiară – este aceeași ecuație liniară pe care ați învățat-o în algebră, probabil enunțată ca y = mx + b.

În ecuația algebrică standard y = mx + b, b era interceptarea lui y, sau valoarea lui y atunci când x era zero. În forma ecuației pe care o folosim, folosim P0 pentru a reprezenta acea cantitate inițială.

În ecuația y = mx + b, amintiți-vă că m era panta. S-ar putea să vă amintiți acest lucru ca fiind „creșterea peste alergare”, sau variația lui y împărțită la variația lui x. În orice caz, reprezintă același lucru ca și diferența comună, d, pe care o folosim – cantitatea pe care se modifică ieșirea Pn atunci când intrarea n crește cu 1.

Ecuațiile y = mx + b și Pn = P0 + d n înseamnă același lucru și pot fi folosite în aceleași moduri. Doar că le scriem oarecum diferit.

Exemple

Populația de elani dintr-o pădure națională a fost măsurată ca fiind de 12.000 în 2003 și a fost măsurată din nou ca fiind de 15.000 în 2007. Dacă populația continuă să crească liniar în acest ritm, care va fi populația de elani în 2014?

Arată soluția

Pentru a începe, trebuie să definim modul în care vom măsura n. Amintiți-vă că P0 este populația atunci când n = 0, deci probabil că nu vrem să folosim literalmente anul 0. Deoarece cunoaștem deja populația din 2003, să definim n = 0 ca fiind anul 2003.

Atunci P0 = 12.000.

În continuare trebuie să găsim d. Amintiți-vă că d este creșterea pe perioadă de timp, în acest caz creșterea pe an. Între cele două măsurători, populația a crescut cu 15.000-12.000 = 3.000, dar a fost nevoie de 2007-2003 = 4 ani pentru a crește atât de mult. Pentru a afla creșterea pe an, putem împărți: 3000 de elani / 4 ani = 750 de elani în 1 an.

Alternativ, puteți folosi formula pantei din algebră pentru a determina diferența comună, observând că populația este rezultatul formulei, iar timpul este intrarea.

d=panta=\frac{\text{schimbarelaieșire}}{\text{schimbarelaintrare}}=\frac{15,000-12,000}{2007-2003}=\frac{3000}{4}=750

Acum putem scrie ecuația noastră în oricare dintre formele preferate.

Forma recursivă

P0 = 12,000

Pn = Pn-1 + 750

Forma explicită

Pn = 12,000 + 750(n)

Pentru a răspunde la întrebare, trebuie să observăm mai întâi că anul 2014 va fi n = 11, deoarece 2014 este la 11 ani după 2003. Forma explicită va fi mai ușor de utilizat pentru acest calcul:

P11 = 12.000 + 750(11) = 20.250 de elanuri

Vezi mai multe despre acest exemplu aici.

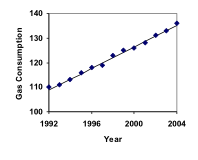
Consumul de benzină în SUA a crescut constant. Datele privind consumul din 1992 până în 2004 sunt prezentate mai jos. Găsiți un model pentru aceste date și folosiți-l pentru a prezice consumul în 2016. Dacă tendința continuă, când va ajunge consumul la 200 de miliarde de galoane?

.

.

Anul ’92 ’93 ’94 ’95 ’96 ’97 ’97 ’98 ’99 ’00 ’01 ’02 ’03 ’04
Consumare (miliarde de galoane) 110 111 113 116 118 119 123 125 125 126 128 131 133 136
Afișați soluția

Plotarea acestor date, se pare că ele au o relație aproximativ liniară:

În timp ce există tehnici statistice mai avansate care pot fi folosite pentru a găsi o ecuație care să modeleze datele, pentru a ne face o idee despre ce se întâmplă, putem găsi o ecuație folosind două bucăți de date – poate datele din 1993 și 2003.

Să lăsăm ca n = 0 să corespundă anului 1993 ar da P0 = 111 miliarde de galoane.

Pentru a găsi d, trebuie să știm cu cât a crescut consumul de gaz în fiecare an, în medie. Din 1993 până în 2003, consumul de gaze a crescut de la 111 miliarde de galoane la 133 miliarde de galoane, o schimbare totală de 133 – 111 = 22 miliarde de galoane, în 10 ani. Aceasta ne dă o variație medie de 22 miliarde de galoane / 10 ani = 2,2 miliarde de galoane pe an.

Echivalent,

d=slope=\frac{\text{modificarea producției}}{\text{modificarea intrării}}=\frac{133-111}{10-0}=\frac{22}{10}=2.2 miliarde de galoane pe an

Acum putem scrie ecuația noastră în orice formă preferată.

Forma recursivă

P0 = 111

Pn = Pn-1 + 2.2

Forma explicită

Pn = 111 + 2.2n

Calcularea valorilor folosind forma explicită și reprezentarea grafică a acestora cu datele originale arată cât de bine se potrivește modelul nostru cu datele.

Acum putem folosi modelul nostru pentru a face predicții despre viitor, presupunând că tendința anterioară continuă neschimbată. Pentru a prezice consumul de benzină în 2016:

n = 23 (2016 – 1993 = 23 ani mai târziu)

P23 = 111 + 2,2(23) = 161,6

Modelul nostru prezice că SUA va consuma 161.6 miliarde de galoane de benzină în 2016, dacă tendința actuală continuă.

Pentru a afla când va ajunge consumul la 200 de miliarde de galoane, vom seta Pn = 200 și vom rezolva pentru n:

Pn = 200 Înlocuiți Pn cu modelul nostru

111 + 2.2n = 200 Se scade 111 din ambele părți

2,2n = 89 Se împarte ambele părți la 2,2

n = 40,4545

Acest lucru ne spune că consumul va ajunge la 200 de miliarde la aproximativ 40 de ani după 1993, ceea ce ar fi în anul 2033.

Etapele pentru a ajunge la acest răspuns sunt detaliate în următorul videoclip.

Costul, în dolari, al unui abonament la sala de sport pentru n luni poate fi descris prin ecuația explicită Pn = 70 + 30n. Ce ne spune această ecuație?

Arată soluția

Valoarea pentru P0 în această ecuație este 70, deci costul inițial de pornire este de 70$. Acest lucru ne spune că trebuie să existe o taxă de inițiere sau de pornire de 70 $ pentru a te înscrie la sala de sport.

Valoarea pentru d în ecuație este 30, deci costul crește cu 30 $ în fiecare lună. Acest lucru ne spune că taxa lunară de înscriere la sala de sport este de 30 de dolari pe lună.

Explicația pentru acest exemplu este detaliată mai jos.

Încercați

Numărul taților care stau acasă în Canada a crescut constant. Deși tendința nu este perfect liniară, ea este destul de liniară. Folosiți datele din 1976 și 2010 pentru a găsi o formulă explicită pentru numărul de tați care stau acasă, apoi folosiți-o pentru a prezice numărul din 2020.

Anul 1976 1984 1991 2000 2010
Nr. de tați care stau la casa părinteascăhome fathers 20610 28725 43530 47665 53555
Show Solution

Lăsând n= 0 să corespundă cu 1976, atunci P_0= 20.610.
Din 1976 până în 2010, numărul taților care stau acasă a crescut cu 53.555 – 20.610 = 32.945
Acest lucru s-a întâmplat pe parcursul a 34 de ani, ceea ce dă un d diferit comun de 32.945 / 34 = 969.
P_n= 20,610 + 969n
Prezentând pentru 2020, folosim n = 44, P(44) = 20,610 + 969(44) = 63,246 tați care stau acasă în 2020.

Când modelele bune devin proaste

Când folosiți modele matematice pentru a prezice comportamentul viitor, este important să țineți cont de faptul că foarte puține tendințe vor continua la nesfârșit.

Exemplu

Să presupunem că un băiat de patru ani are în prezent o înălțime de 39 de centimetri și vi se spune să vă așteptați ca el să crească cu 2,5 centimetri pe an.

Putem stabili un model de creștere, cu n = 0 corespunzând vârstei de 4 ani.

Forma recursivă

P0 = 39

Pn = Pn-1 + 2,5

Forma explicită

Pn = 39 + 2.5(n)

Atunci, la vârsta de 6 ani, ne-am aștepta ca el să aibă

P2 = 39 + 2,5(2) = 44 de centimetri înălțime

Care model matematic se va descompune în cele din urmă. Cu siguranță, nu ar trebui să ne așteptăm ca acest băiat să continue să crească în același ritm toată viața lui. Dacă ar fi făcut-o, la vârsta de 50 de ani ar fi

P46 = 39 + 2,5(46) = 154 de centimetri înălțime = 12,8 picioare înălțime!

Când folosim orice model matematic, trebuie să luăm în considerare ce date de intrare sunt rezonabile de utilizat. Ori de câte ori extrapolăm sau facem predicții în viitor, presupunem că modelul va continua să fie valabil.

Vezi aici o explicație video a acestei descompuneri a modelului de creștere liniară.

Creștere exponențială (geometrică )

Creștere a populației

Să presupunem că, în fiecare an, doar 10% din peștii dintr-un lac au urmași supraviețuitori. Dacă anul trecut erau 100 de pești în lac, acum ar fi 110 pești. Dacă anul trecut au fost 1000 de pești în lac, acum ar fi 1100 de pești. În absența oricăror factori inhibitori, populațiile de oameni și animale tind să crească în fiecare an cu un procent din populația existentă.


Să presupunem că lacul nostru a început cu 1000 de pești, iar 10% dintre pești au urmași supraviețuitori în fiecare an. Deoarece începem cu 1000 de pești, P0 = 1000. Cum calculăm P1? Noua populație va fi vechea populație, plus încă 10%. Simbolic:

P1 = P0 + 0,10P0

Atenție, acest lucru ar putea fi condensat într-o formă mai scurtă prin factorizare:

P1 = P0 + 0,10P0 = 1P0 + 0,10P0 = (1+ 0,10)P0 = 1,10P0

În timp ce 10% este rata de creștere, 1,10 este multiplicatorul de creștere. Observați că 1,10 poate fi considerat ca fiind „procentul inițial de 100% plus încă 10%.”

Pentru populația noastră de pești,

P1 = 1,10(1000) = 1100

Am putea apoi calcula populația în anii următori:

P2 = 1.10P1 = 1.10(1100) = 1210

P3 = 1.10P2 = 1.10(1210) = 1331

Observați că, în primul an, populația a crescut cu 100 de pești; în al doilea an, populația a crescut cu 110 pești; iar în al treilea an, populația a crescut cu 121 de pești.

În timp ce există o creștere procentuală constantă, creșterea reală a numărului de pești este în creștere în fiecare an.

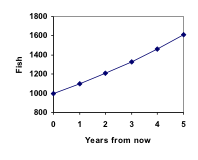
Graficând aceste valori, vedem că această creștere nu pare chiar liniară.

O trecere în revistă a acestui scenariu cu pești poate fi vizualizată aici:

Pentru a avea o imagine mai bună a modului în care această creștere procentuală afectează lucrurile, avem nevoie de o formă explicită, astfel încât să putem calcula rapid valorile mai departe în viitor.

La fel cum am făcut pentru modelul liniar, vom începe să construim pornind de la ecuația recursivă:

P1 = 1.10(P0 )= 1.10(1000)

P2 = 1.10(P1 )= 1.10(1.10(1000)) = 1.102(1000)

P3 = 1.10(P2 )= 1.10(1.102(1000)) = 1.103(1000)

P4 = 1.10(P3 )= 1.10(1.103(1000)) = 1.104(1000)

Observând un model, putem generaliza forma explicită ca fiind:

Pn = 1.10n(1000), sau, în mod echivalent, Pn = 1000(1.10n)

De aici, putem calcula rapid numărul de pești în 10, 20 sau 30 de ani:

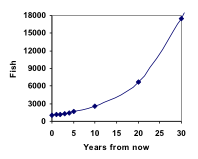
P10 = 1.1010(1000) = 2594

P20 = 1.1020(1000) = 6727

P30 = 1.1030(1000) = 17449

Adăugând aceste valori la graficul nostru, rezultă o formă care cu siguranță nu este liniară. Dacă populația noastră de pești ar fi crescut liniar, cu 100 de pești în fiecare an, populația ar fi ajuns la doar 4000 în 30 de ani, în comparație cu aproape 18.000 cu această creștere bazată pe procente, numită creștere exponențială.

Un videoclip care demonstrează modelul explicit al acestei povești cu pești poate fi vizionat aici:

În creșterea exponențială, populația crește proporțional cu mărimea populației, astfel încât, pe măsură ce populația devine mai mare, aceeași creștere procentuală va produce o creștere numerică mai mare.

Creștere exponențială

Dacă o cantitate începe de la mărimea P0 și crește cu R% (scris ca o zecimală, r) în fiecare perioadă de timp, atunci cantitatea după n perioade de timp poate fi determinată folosind oricare dintre aceste relații:

Forma recursivă

Pn = (1+r) Pn-1

Forma explicită

Pn = (1+r)n P0 sau, în mod echivalent, Pn = P0 (1+r)n

Noi numim r rata de creștere.

Termenul (1+r) se numește multiplicator de creștere sau raport comun.

Exemplu

Între 2007 și 2008, Olympia, WA a crescut cu aproape 3%, ajungând la o populație de 245 de mii de locuitori. Dacă această rată de creștere ar continua, care ar fi populația din Olympia în 2014?

Arată soluția

Ca și înainte, trebuie mai întâi să definim ce an va corespunde lui n = 0. Deoarece cunoaștem populația din 2008, ar fi logic ca anul 2008 să corespundă lui n = 0, deci P0 = 245.000 de locuitori. Anul 2014 ar fi atunci n = 6.

Știm că rata de creștere este de 3%, ceea ce dă r = 0,03.

Utilizând forma explicită:

P6 = (1+0,03)6 (245.000) = 1,19405(245.000) = 292.542,25

Modelul prezice că, în 2014, Olympia va avea o populație de aproximativ 293 de mii de persoane.

Video-ul următor explică acest exemplu în detaliu.

Evaluarea exponenților la calculator

Pentru a evalua expresii precum (1,03)6, va fi mai ușor să folosiți un calculator decât să înmulțițiți 1,03 cu el însuși de șase ori. Majoritatea calculatoarelor științifice au un buton pentru exponenți. Acesta este de obicei fie etichetat astfel:

^ , yx , sau xy .

Pentru a evalua 1,036 vom tasta 1,03 ^ 6, sau 1,03 yx 6. Încercați – ar trebui să obțineți un răspuns în jur de 1,1940523.

Încercați

India este a doua cea mai populată țară din lume, cu o populație în 2008 de aproximativ 1,14 miliarde de locuitori. Populația crește cu aproximativ 1,34% în fiecare an. Dacă această tendință continuă, la cât va crește populația Indiei până în 2020?

Arată soluția

Utilizând n = 0 corespunzător anului 2008, P_12= (1+0,0134)12(1,14) = aproximativ 1.337 miliarde de oameni în 2020

Exemple

Un prieten folosește ecuația Pn = 4600(1,072)n pentru a prezice taxa anuală de școlarizare la un colegiu local. Ea spune că formula se bazează pe anii de după 2010. Ce ne spune această ecuație?

Arată soluția

În ecuație, P0 = 4600, care este valoarea inițială a taxei de școlarizare atunci când n = 0. Acest lucru ne spune că taxa de școlarizare în 2010 a fost de 4.600 $.

Multiplicatorul de creștere este 1,072, deci rata de creștere este 0,072, sau 7,2%. Acest lucru ne spune că se așteaptă ca taxele de școlarizare să crească cu 7,2% în fiecare an.

Punând toate acestea împreună, am putea spune că taxele de școlarizare în 2010 au fost de 4 600 de dolari și se așteaptă să crească cu 7,2% în fiecare an.

Veziți următorul exemplu pentru a vedea acest exemplu prelucrat.

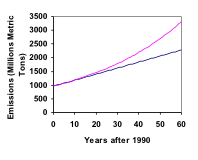
În 1990, consumul de energie rezidențială în SUA a fost responsabil pentru 962 de milioane de tone metrice de emisii de dioxid de carbon. Până în anul 2000, acest număr a crescut la 1182 milioane de tone metrice. Dacă emisiile cresc exponențial și continuă în același ritm, la cât vor ajunge emisiile până în 2050?

Arată soluția

La fel ca înainte, vom face să corespundă n = 0 cu 1990, deoarece acesta este anul pentru primele date pe care le avem. Aceasta va face ca P0 = 962 (milioane de tone metrice de CO2). În această problemă, nu ni se dă rata de creștere, dar în schimb ni se dă că P10 = 1182.

Când n = 10, ecuația explicită arată astfel:

P10 = (1+r)10 P0

Cunoaștem valoarea pentru P0, așa că o putem introduce în ecuație:

P10 = (1+r)10 962

Știm, de asemenea, că P10 = 1182, așa că, înlocuind-o, obținem

1182 = (1+r)10 962

Acum putem rezolva această ecuație pentru rata de creștere, r. Începeți prin a împărți cu 962.

\frac{1182}{962}={{{(1+r)}^{10}}}. Luați rădăcina a 10-a a ambelor părți

\sqrt{\frac{1182}{962}}=1+r Scădeți 1 din ambele părți

r=\sqrt{\frac{1182}{962}}-1=0,0208 = 2,08%

Atunci, dacă emisiile cresc exponențial, ele cresc cu aproximativ 2,08% pe an. Acum putem prezice emisiile din 2050, găsind P60

P60 = (1+0,0208)60 962 = 3308,4 milioane de tone metrice de CO2 în 2050

Vezi mai multe despre acest exemplu aici.

Arontare

Ca o notă despre rotunjire, observați că, dacă am fi rotunjit rata de creștere la 2,1%, calculul nostru pentru emisiile din 2050 ar fi fost 3347. Rotunjirea la 2% ar fi schimbat rezultatul nostru la 3156. O diferență foarte mică în ceea ce privește ratele de creștere se amplifică foarte mult în cazul creșterii exponențiale. Din acest motiv, se recomandă să rotunjiți rata de creștere cât mai puțin posibil.

Dacă trebuie să rotunjiți, păstrați cel puțin trei cifre semnificative – numere după orice zerouri de început. Astfel, 0,4162 ar putea fi rotunjit în mod rezonabil la 0,416. O rată de creștere de 0,001027 ar putea fi rotunjită în mod rezonabil la 0,00103.

Evaluarea rădăcinilor pe calculator

În exemplul anterior, a trebuit să calculăm rădăcina a 10-a a unui număr. Acest lucru este diferit de a lua rădăcina pătrată de bază, √. Multe calculatoare științifice au un buton pentru rădăcini generale. Acesta este de obicei etichetat astfel:

\sqrt{x}

Pentru a evalua a 3-a rădăcină a lui 8, de exemplu, am tasta fie 3 \sqrt{{}} 8, fie 8 \sqrt{{}}. 3, în funcție de calculator. Încercați pe al dumneavoastră pentru a vedea ce să folosiți – ar trebui să obțineți un răspuns de 2.

Dacă calculatorul dumneavoastră nu are un buton de rădăcină generală, nu este totul pierdut. În schimb, puteți folosi proprietatea exponenților care afirmă că:

\sqrt{a}={a}^{\frac{1}{2}}.

Așa, pentru a calcula rădăcina a 3-a a lui 8, ați putea folosi tasta de exponenți a calculatorului dumneavoastră pentru a evalua 81/3. Pentru a face acest lucru, tastați:

8 yx ( 1 ÷ 3 )

Parantezele îi spun calculatorului să împartă 1/3 înainte de a face exponentul.

Încercați

Numărul de utilizatori ai unei rețele de socializare era de 45 de mii în februarie, când au devenit oficial publice, și a crescut la 60 de mii până în octombrie. Dacă site-ul crește exponențial, iar creșterea continuă în același ritm, la câți utilizatori ar trebui să se aștepte la doi ani după ce au devenit public?

Arată soluția

Aici vom măsura n în luni și nu în ani, cu n = 0 corespunzând lunii februarie când au devenit publici. Acest lucru dă P_0= 45 de mii. Octombrie este 8 luni mai târziu, deci P_8= 60.
P_8=(1+r)^{8}P_0
60=(1+r)^{8}45
\frac{60}{45}=(1+r)^8
\sqrt{\frac{60}{45}}=1+r
r=\sqrt{\frac{60}{45}}-1=0.0366\text{ sau }3,66%
Ecuația generală explicită este P_n =(1,0366)^{n}45. Predicția la 24 de luni după ce au devenit publici dă P_{24}=(1,0366)^{24}45=106,63 mii de utilizatori.

Exemplu

Răsfoind la ultimul exemplu, pentru comparație, care ar fi emisiile de carbon în 2050 dacă emisiile ar crește liniar în același ritm?

Arată soluția

Din nou vom obține că n = 0 corespunde cu 1990, ceea ce dă P0 = 962. Pentru a găsi d, am putea adopta aceeași abordare ca mai devreme, observând că emisiile au crescut cu 220 de milioane de tone metrice în 10 ani, ceea ce dă o diferență comună de 22 de milioane de tone metrice în fiecare an.

Alternativ, am putea folosi o abordare similară cu cea pe care am folosit-o pentru a găsi ecuația exponențială. Când n = 10, ecuația liniară explicită arată astfel:

P10 = P0 + 10d

Cunoaștem valoarea lui P0, așa că o putem introduce în ecuație:

P10 = 962 + 10d

Din moment ce știm că P10 = 1182, înlocuind-o obținem

1182 = 962 + 10d

Acum putem rezolva această ecuație pentru diferența comună, d.

1182 – 962 = 10d

220 = 10d

d = 22

Aceasta ne spune că, dacă emisiile se modifică liniar, ele cresc cu 22 de milioane de tone metrice în fiecare an. Prezicând emisiile în 2050,

P60 = 962 + 22(60) = 2282 milioane de tone metrice.

Vă veți observa că acest număr este substanțial mai mic decât predicția din modelul de creștere exponențială. Calcularea și reprezentarea grafică a mai multor valori ajută la ilustrarea diferențelor.

O demonstrație a acestui exemplu poate fi văzută în următorul videoclip.

Atunci cum știm ce model de creștere să folosim atunci când lucrăm cu date? Există două abordări care ar trebui să fie folosite împreună ori de câte ori este posibil:

  1. Căutați mai mult de două bucăți de date. Reprezentați grafic valorile și căutați o tendință. Datele par să se schimbe ca o linie, sau valorile par să se curbeze în sus?
  2. Considerați factorii care contribuie la date. Sunt lucruri la care v-ați aștepta să se schimbe liniar sau exponențial? De exemplu, în cazul emisiilor de carbon, ne-am putea aștepta ca, în lipsa altor factori, acestea să fie strâns legate de valorile populației, care tind să se schimbe exponențial.

.

By: adminPosted on

Lasă un răspuns

Adresa ta de email nu va fi publicată.