Mathematics for the Liberal Arts

Mając stałą szybkość zmian jest cechą definiującą wzrost liniowy. Wykreślenie par współrzędnych związanych ze stałą zmianą da w rezultacie linię prostą, kształt wzrostu liniowego. W tym rozdziale sformalizujemy sposób opisania wzrostu liniowego przy użyciu terminów i pojęć matematycznych. Do końca tego rozdziału, będziesz w stanie napisać zarówno rekurencyjne i jawne równania dla wzrostu liniowego, biorąc pod uwagę warunki początkowe lub stałą zmiany. Będziesz także w stanie rozpoznać różnicę między wzrostem liniowym i geometrycznym na podstawie wykresu lub równania.

Wzrost liniowy (algebraiczny)

Przewidywanie wzrostu

Marco jest kolekcjonerem zabytkowych butelek z wodą sodową. Jego kolekcja zawiera obecnie 437 butelek. Co roku przeznacza w budżecie wystarczająco dużo pieniędzy, aby kupić 32 nowe butelki. Czy możemy określić, ile butelek będzie miał za 5 lat i jak długo potrwa, zanim jego kolekcja osiągnie 1000 butelek?

Prawdopodobnie można rozwiązać oba te pytania bez równania lub formalnej matematyki, ale zamierzamy sformalizować nasze podejście do tego problemu, aby zapewnić środki do odpowiedzi na bardziej skomplikowane pytania.

Załóżmy, że Pn reprezentuje liczbę lub populację butelek, które Marco ma po n latach. Tak więc P0 reprezentowałoby liczbę butelek teraz, P1 reprezentowałoby liczbę butelek po 1 roku, P2 reprezentowałoby liczbę butelek po 2 latach, i tak dalej. Możemy opisać jak zmienia się kolekcja butelek Marco używając:

P0 = 437

Pn = Pn-1 + 32

To się nazywa relacja rekurencyjna. Relacja rekurencyjna to formuła, która odnosi następną wartość w sekwencji do poprzednich wartości. Tutaj, liczba butelek w roku n może być znaleziona przez dodanie 32 do liczby butelek w poprzednim roku, Pn-1. Korzystając z tej zależności, moglibyśmy obliczyć:

P1 = P0 + 32 = 437 + 32 = 469

P2 = P1 + 32 = 469 + 32 = 501

P3 = P2 + 32 = 501 + 32 = 533

P4 = P3. + 32 = 533 + 32 = 565

P5 = P4 + 32 = 565 + 32 = 597

Odpowiedzieliśmy na pytanie, ile butelek będzie miał Marco za 5 lat.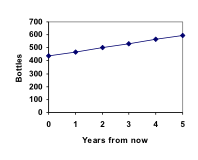

Jednakże rozwiązanie, ile czasu zajmie jego kolekcji osiągnięcie 1000 butelek, wymagałoby znacznie więcej obliczeń.

Jakkolwiek zależności rekurencyjne są doskonałe do prostego i czystego opisywania zmian wielkości, nie są wygodne do przewidywania lub rozwiązywania problemów, które sięgają daleko w przyszłość. Do tego celu preferowana jest zamknięta lub jawna forma dla relacji. Równanie jawne pozwala nam obliczyć Pn bezpośrednio, bez konieczności znajomości Pn-1. Być może jesteś już w stanie odgadnąć jawne równanie, ale spróbujmy wyprowadzić je z formuły rekurencyjnej. Możemy to zrobić, selektywnie nie upraszczając, gdy idziemy:

P1 = 437 + 32 = 437 + 1(32)

P2 = P1 + 32 = 437 + 32 + 32 = 437 + 2(32)

P3 = P2 + 32 = (437 + 2(32)) + 32 = 437 + 3(32)

P4 = P3 + 32 = (437 + 3(32)) + 32 = 437 + 4(32)

Możesz pewnie teraz zobaczyć wzór i uogólnić, że

Pn = 437 + n(32) = 437 + 32n

Korzystając z tego równania, możemy obliczyć, ile butelek będzie miał po 5 latach:

P5 = 437 + 32(5) = 437 + 160 = 597

Możemy teraz również rozwiązać, kiedy kolekcja osiągnie 1000 butelek, podstawiając 1000 za Pn i rozwiązując równanie n

1000 = 437 + 32n

563 = 32n

n = 563/32 = 17.59

Więc Marco osiągnie 1000 butelek w ciągu 18 lat.

Kroki wyznaczania wzoru i rozwiązywania problemu kolekcji butelek Marco są szczegółowo wyjaśnione w kolejnych filmach.

W tym przykładzie kolekcja Marco rosła co roku o tę samą liczbę butelek. Ta stała zmiana jest cechą definiującą wzrost liniowy. Wykreślając wartości, które obliczyliśmy dla kolekcji Marco, widzimy, że wartości te tworzą linię prostą, kształt wzrostu liniowego.

Przykłady

Populacja łosi w lesie narodowym została zmierzona na 12 000 w 2003 roku, i została ponownie zmierzona na 15 000 w 2007 roku. Jeśli populacja nadal będzie rosła liniowo w tym tempie, to ile wyniesie populacja łosi w 2014 roku?

Pokaż rozwiązanie

Na początek musimy określić, jak będziemy mierzyć n. Pamiętajmy, że P0 to populacja, gdy n = 0, więc prawdopodobnie nie chcemy dosłownie używać roku 0. Ponieważ znamy już populację w 2003 roku, zdefiniujmy n = 0 jako rok 2003.

Wtedy P0 = 12 000.

Następnie musimy znaleźć d. Pamiętajmy, że d jest wzrostem na okres czasu, w tym przypadku wzrostem na rok. Pomiędzy tymi dwoma pomiarami populacja wzrosła o 15,000-12,000 = 3,000, ale zajęło to 2007-2003 = 4 lata, aby wzrosnąć tak bardzo. Aby znaleźć wzrost na rok, możemy podzielić: 3000 łosi / 4 lata = 750 łosi w ciągu 1 roku.

Alternatywnie, możesz użyć wzoru nachylenia z algebry, aby określić wspólną różnicę, zauważając, że populacja jest wyjściem wzoru, a czas jest wejściem.

d=slope==frac{tekst{zmianawyjścia}}{tekst{zmianawejścia}}=frac{15,000-12,000}{2007-2003}==frac{3000}{4}=750

Możemy teraz zapisać nasze równanie w dowolnej preferowanej formie.

Forma rekursywna

P0 = 12,000

Pn = Pn-1 + 750

Forma jawna

Pn = 12,000 + 750(n)

Aby odpowiedzieć na pytanie, musimy najpierw zauważyć, że rok 2014 będzie n = 11, ponieważ rok 2014 jest 11 lat po roku 2003. Do tych obliczeń łatwiej będzie użyć postaci jawnej:

P11 = 12 000 + 750(11) = 20 250 łosi

Zobacz więcej o tym przykładzie tutaj.

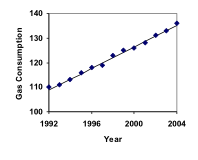
Zużycie benzyny w USA stale rośnie. Dane dotyczące konsumpcji od 1992 do 2004 roku są pokazane poniżej. Znajdź model dla tych danych i użyj go, aby przewidzieć zużycie w 2016 roku. Jeśli trend się utrzyma, kiedy konsumpcja osiągnie 200 miliardów galonów?

.

Rok	’92	’93	’94	’95	’96	’97	’98	’99	’00	’01	’02	’03	’04
Zużycie (mld. galonów)	110	111	113	116	118	119	123	125	126	128	131	133	136

Pokaż rozwiązanie

Plotting this data, wydaje się, że mają one w przybliżeniu liniową zależność:

Choć istnieją bardziej zaawansowane techniki statystyczne, których można użyć do znalezienia równania modelującego dane, aby uzyskać wyobrażenie o tym, co się dzieje, możemy znaleźć równanie, używając dwóch fragmentów danych – być może danych z 1993 i 2003 roku.

Ustawienie n = 0 odpowiada 1993 r. dałoby P0 = 111 miliardów galonów.

Aby znaleźć d, musimy wiedzieć, o ile średnio wzrosło zużycie gazu w każdym roku. Od 1993 do 2003 roku zużycie gazu wzrosło z 111 miliardów galonów do 133 miliardów galonów, całkowita zmiana 133 – 111 = 22 miliardów galonów, w ciągu 10 lat. Daje nam to średnią zmianę 22 miliardy galonów / 10 lat = 2,2 miliarda galonów rocznie.

Równoważnie,

d=slope==}frac{tekst{zmianawyjścia}}{}}=}frac{133-111}{10-0}=}frac{22}{10}=2.2 miliardy galonów rocznie

Możemy teraz zapisać nasze równanie w dowolnej preferowanej formie.

Forma rekursywna

P0 = 111

Pn = Pn-1 + 2.2

Forma explicite

Pn = 111 + 2.2n

Obliczenie wartości przy użyciu formy explicite i wykreślenie ich z oryginalnymi danymi pokazuje, jak dobrze nasz model pasuje do danych.

Możemy teraz użyć naszego modelu do przewidywań dotyczących przyszłości, zakładając, że poprzedni trend pozostanie niezmieniony. Aby przewidzieć zużycie benzyny w 2016 roku:

n = 23 (2016 – 1993 = 23 lata później)

P23 = 111 + 2,2(23) = 161,6

Nasz model przewiduje, że USA zużyją 161.6 miliardów galonów benzyny w 2016 roku, jeśli obecny trend się utrzyma.

Aby znaleźć, kiedy zużycie osiągnie 200 miliardów galonów, ustawilibyśmy Pn = 200, i rozwiązali dla n:

Pn = 200 Zastąp Pn naszym modelem

111 + 2.2n = 200 Odejmij 111 od obu stron

2.2n = 89 Podziel obie strony przez 2.2

n = 40.4545

To mówi nam, że konsumpcja osiągnie 200 miliardów około 40 lat po 1993 roku, czyli w roku 2033.

Kroki prowadzące do tej odpowiedzi są szczegółowo opisane w poniższym filmie.

Koszt, w dolarach, członkostwa w siłowni przez n miesięcy może być opisany przez jawne równanie Pn = 70 + 30n. Co mówi nam to równanie?

Pokaż rozwiązanie

Wartość P0 w tym równaniu wynosi 70, więc początkowy koszt początkowy wynosi 70$. To mówi nam, że musi istnieć opłata inicjacyjna lub początkowa w wysokości 70 dolarów, aby dołączyć do siłowni.

Wartość d w równaniu wynosi 30, więc koszt wzrasta o 30 dolarów każdego miesiąca. To mówi nam, że miesięczna opłata za członkostwo w siłowni wynosi $30 miesięcznie.

Wyjaśnienie tego przykładu jest szczegółowo opisane poniżej.

Kiedy dobre modele się psują

Kiedy używamy modeli matematycznych do przewidywania przyszłego zachowania, ważne jest, aby pamiętać, że bardzo niewiele trendów będzie trwało w nieskończoność.

wzrost wykładniczy (geometryczny)

wzrost populacji

Załóżmy, że każdego roku, tylko 10% ryb w jeziorze ma przeżywające potomstwo. Jeśli w zeszłym roku w jeziorze było 100 ryb, to teraz będzie ich 110. Jeśli w zeszłym roku w jeziorze było 1000 ryb, to teraz będzie 1100 ryb. Bez żadnych czynników hamujących, populacje ludzi i zwierząt mają tendencję do wzrostu o pewien procent istniejącej populacji każdego roku.

Załóżmy, że nasze jezioro zaczęło się od 1000 ryb, a 10% ryb ma żyjące potomstwo każdego roku. Ponieważ zaczynamy z 1000 ryb, P0 = 1000. Jak obliczymy P1? Nowa populacja będzie starą populacją, plus dodatkowe 10%. Symbolicznie:

P1 = P0 + 0.10P0

Zauważ, że można to skondensować do krótszej postaci przez faktoryzację:

P1 = P0 + 0.10P0 = 1P0 + 0.10P0 = (1+ 0.10)P0 = 1.10P0

Podczas gdy 10% to stopa wzrostu, 1.10 to mnożnik wzrostu. Zauważmy, że 1.10 może być rozumiane jako „oryginalne 100% plus dodatkowe 10%.”

Dla naszej populacji ryb,

P1 = 1.10(1000) = 1100

Możemy wtedy obliczyć populację w późniejszych latach:

P2 = 1,10P1 = 1,10(1100) = 1210

P3 = 1,10P2 = 1,10(1210) = 1331

Zauważmy, że w pierwszym roku populacja wzrosła o 100 ryb; w drugim roku populacja wzrosła o 110 ryb; a w trzecim roku populacja wzrosła o 121 ryb.

Pomimo że mamy do czynienia ze stałym wzrostem procentowym, to rzeczywisty przyrost liczby ryb rośnie z każdym rokiem.

Grafikując te wartości widzimy, że ten wzrost nie do końca wydaje się liniowy.

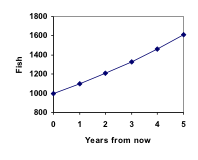
Przewodnik po tym scenariuszu rybnym można obejrzeć tutaj:

Aby uzyskać lepszy obraz tego, jak ten procentowy wzrost wpływa na rzeczy, potrzebujemy jawnej formy, więc możemy szybko obliczyć wartości dalej w przyszłości.

Tak jak zrobiliśmy to dla modelu liniowego, zaczniemy budować od równania rekurencyjnego:

P1 = 1.10(P0 )= 1.10(1000)

P2 = 1.10(P1 )= 1.10(1.10(1000)) = 1.102(1000)

P3 = 1.10(P2 )= 1.10(1.102(1000)) = 1.103(1000)

P4 = 1.10(P3 )= 1.10(1.103(1000)) = 1.104(1000)

Obserwując wzór, możemy uogólnić postać jawną do postaci:

Pn = 1.10n(1000), lub równoważnie, Pn = 1000(1.10n)

W oparciu o to możemy szybko obliczyć liczbę ryb w ciągu 10, 20, lub 30 lat:

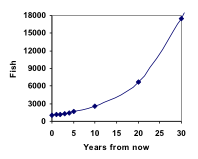
P10 = 1.1010(1000) = 2594

P20 = 1.1020(1000) = 6727

P30 = 1.1030(1000) = 17449

Dodając te wartości do naszego wykresu widzimy kształt, który zdecydowanie nie jest liniowy. Gdyby nasza populacja ryb rosła liniowo, o 100 ryb każdego roku, populacja osiągnęłaby tylko 4000 w ciągu 30 lat, w porównaniu do prawie 18 000 z tym procentowym wzrostem, zwanym wzrostem wykładniczym.

Film demonstrujący wyraźny model tej historii ryb można obejrzeć tutaj:

W wzroście wykładniczym, populacja rośnie proporcjonalnie do wielkości populacji, więc jak populacja staje się większa, ten sam wzrost procentowy przyniesie większy wzrost liczbowy.

Try It

Indie są drugim najludniejszym krajem na świecie, z populacją w 2008 roku około 1,14 miliarda ludzi. Liczba ludności rośnie o około 1,34% każdego roku. Jeśli ta tendencja się utrzyma, to do jakiej liczby wzrośnie populacja Indii do roku 2020?

Pokaż rozwiązanie

Używając n = 0 odpowiadającego 2008, P_12= (1+0,0134)12(1,14) = około 1.337 miliardów ludzi w 2020 roku

Przykłady

Przyjaciółka używa równania Pn = 4600(1,072)n, aby przewidzieć roczne czesne w lokalnym college’u. Mówi, że wzór opiera się na latach, w których odbywały się zajęcia. Mówi, że wzór jest oparty na latach po roku 2010. Co mówi nam to równanie?

Pokaż rozwiązanie

W równaniu, P0 = 4600, które jest wartością początkową czesnego, gdy n = 0. To mówi nam, że czesne w 2010 roku wynosiło 4600 dolarów.

Mnożnik wzrostu wynosi 1,072, więc stopa wzrostu wynosi 0,072, lub 7,2%. To mówi nam, że oczekuje się, że czesne będzie rosło o 7,2% każdego roku.

Połączenie tego razem, możemy powiedzieć, że czesne w 2010 roku wynosiło $4,600 i oczekuje się, że będzie rosło o 7,2% każdego roku.

Zobacz poniższe, aby zobaczyć ten przykład opracowany.

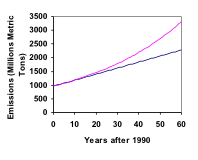
W 1990 roku, zużycie energii w budynkach mieszkalnych w USA było odpowiedzialne za 962 miliony ton metrycznych emisji dwutlenku węgla. Do roku 2000, liczba ta wzrosła do 1182 milionów ton metrycznych. Jeśli emisja rośnie wykładniczo i kontynuuje w tym samym tempie, to do czego wzrośnie do roku 2050?

Pokaż rozwiązanie

Podobnie jak poprzednio, będziemy odpowiadać n = 0 z rokiem 1990, ponieważ jest to rok dla pierwszego kawałka danych, które mamy. To da nam P0 = 962 (mln ton metrycznych CO2). W tym problemie nie podano nam stopy wzrostu, ale zamiast tego podano nam, że P10 = 1182.

Gdy n = 10, jawne równanie wygląda następująco:

P10 = (1+r)10 P0

Znamy wartość dla P0, więc możemy ją wstawić do równania:

P10 = (1+r)10 962

Wiemy też, że P10 = 1182, więc podstawiając to, otrzymujemy

1182 = (1+r)10 962

Możemy teraz rozwiązać to równanie dla stopy wzrostu, r. Zacznij od podzielenia przez 962.

frac{1182}{962}={{(1+r)}^{10}}. Weź 10 pierwiastek z obu stron

r==1+r Odejmij 1 od obu stron

r===1+r=0.0208 = 2.08%

Więc jeśli emisje rosną wykładniczo, to rosną o około 2.08% rocznie. Możemy teraz przewidzieć emisje w 2050 roku znajdując P60

P60 = (1+0.0208)60 962 = 3308.4 mln ton metrycznych CO2 w 2050 roku

Zobacz więcej o tym przykładzie tutaj.

Zaokrąglanie

Jako uwaga na temat zaokrąglania, zauważ, że gdybyśmy zaokrąglili stopę wzrostu do 2,1%, nasze obliczenia dla emisji w 2050 roku wyniosłyby 3347. Zaokrąglenie do 2% zmieniłoby nasz wynik na 3156. Bardzo mała różnica w stopach wzrostu ulega znacznemu powiększeniu w przypadku wzrostu wykładniczego. Z tego powodu zaleca się zaokrąglanie tempa wzrostu tak mało, jak to możliwe.

Jeśli musisz zaokrąglić, zachowaj co najmniej trzy znaczące cyfry – liczby po wszelkich zerach wiodących. Więc 0.4162 może być rozsądnie zaokrąglone do 0.416. Stopa wzrostu 0.001027 może być rozsądnie zaokrąglona do 0.00103.

Ocena pierwiastków na kalkulatorze

W poprzednim przykładzie, musieliśmy obliczyć dziesiąty pierwiastek z liczby. Jest to coś innego niż obliczanie podstawowego pierwiastka kwadratowego, √. Wiele kalkulatorów naukowych posiada przycisk do obliczania pierwiastków ogólnych. Zazwyczaj jest on oznaczony następująco:

Sqrt{x}

Aby obliczyć trzeci pierwiastek z 8, na przykład, wpisujemy albo 3 \sqrt{{} 8, lub 8 \sqrt{{} 3, w zależności od kalkulatora. Wypróbuj to na swoim, aby zobaczyć, którego użyć – powinieneś otrzymać odpowiedź 2.

Jeśli twój kalkulator nie ma przycisku pierwiastka ogólnego, nie wszystko jest stracone. Aby to zrobić, wpisz:

8 yx ( 1 ÷ 3 )

Nawiasy mówią kalkulatorowi, aby podzielił 1/3 przed wykonaniem wykładnika.

Spróbuj

Liczba użytkowników pewnego portalu społecznościowego wynosiła 45 tysięcy w lutym, kiedy został on oficjalnie upubliczniony, i wzrosła do 60 tysięcy do października. Jeśli witryna rośnie wykładniczo, a wzrost jest kontynuowany w tym samym tempie, ilu użytkowników należy się spodziewać dwa lata po jej upublicznieniu?

Pokaż rozwiązanie

W tym przypadku będziemy mierzyć n w miesiącach, a nie latach, przy czym n = 0 odpowiada lutemu, kiedy witryna została upubliczniona. Daje to P_0= 45 tysięcy. Październik jest o 8 miesięcy później, więc P_8= 60.
P_8=(1+r)^{8}P_0
60=(1+r)^{8}45
P_0=(1+r)^8
P_0=(1+r)^8
P_8=1+r
r=P_0=(1+r)^{8}45
P_0
60=(1+r)^{8}45
P_0
60=(1+r)^{8}45
P_0=(1+r)^8}.0366 lub 3,66%
Ogólne równanie jawne to P_n =(1,0366)^{n}45. Przewidywanie 24 miesięcy po ich upublicznieniu daje P_{24}=(1.0366)^{24}45=106,63 tys. użytkowników.

Przykład

Patrząc na ostatni przykład, dla porównania, jaka byłaby emisja dwutlenku węgla w 2050 roku, gdyby emisja rosła liniowo w tym samym tempie?

Pokaż rozwiązanie

Ponownie otrzymamy n = 0 odpowiadające 1990, co daje P0 = 962. Aby znaleźć d, możemy zastosować to samo podejście co wcześniej, zauważając, że emisja wzrosła o 220 milionów ton metrycznych w ciągu 10 lat, co daje wspólną różnicę 22 milionów ton metrycznych każdego roku.

Alternatywnie, możemy zastosować podejście podobne do tego, które wykorzystaliśmy do znalezienia równania wykładniczego. Gdy n = 10, jawne równanie liniowe wygląda następująco:

P10 = P0 + 10d

Znamy wartość dla P0, więc możemy ją wstawić do równania:

P10 = 962 + 10d

Ponieważ wiemy, że P10 = 1182, podstawiając to otrzymujemy

1182 = 962 + 10d

Możemy teraz rozwiązać to równanie dla różnicy wspólnej, d.

1182 – 962 = 10d

220 = 10d

d = 22

To mówi nam, że jeśli emisje zmieniają się liniowo, to rosną o 22 miliony ton metrycznych każdego roku. Przewidując emisję w 2050 roku,

P60 = 962 + 22(60) = 2282 mln ton metrycznych.

Zauważ, że ta liczba jest znacznie mniejsza niż przewidywania z modelu wzrostu wykładniczego. Obliczenie i wykreślenie większej liczby wartości pomoże zilustrować różnice.

Demonstrację tego przykładu można zobaczyć na poniższym filmie.

Więc skąd mamy wiedzieć, którego modelu wzrostu użyć podczas pracy z danymi? Istnieją dwa podejścia, które powinny być stosowane razem, gdy tylko jest to możliwe:

1. Znajdź więcej niż dwa kawałki danych. Wykreśl wartości i poszukaj trendu. Czy dane wydają się zmieniać jak linia, czy wartości wydają się być zakrzywione w górę?
2. Zastanów się nad czynnikami wpływającymi na dane. Czy są to rzeczy, których spodziewałbyś się zmieniać liniowo lub wykładniczo? Na przykład, w przypadku emisji dwutlenku węgla, moglibyśmy oczekiwać, że przy braku innych czynników, byłyby one ściśle związane z wartościami populacji, które mają tendencję do zmian wykładniczych.

.