Risultati dell’apprendimento

  • Determinare se i dati o uno scenario descrivono una crescita lineare o geometrica
  • Identificare i tassi di crescita, i valori iniziali o i valori puntuali espressi verbalmente, graficamente, o numericamente, e tradurli in un formato utilizzabile nel calcolo
  • Calcolare equazioni ricorsive ed esplicite per la crescita lineare e geometrica date informazioni sufficienti, e usare queste equazioni per fare previsioni

Avere un tasso di cambiamento costante è la caratteristica che definisce la crescita lineare. Tracciando coppie di coordinate associate a un cambiamento costante si otterrà una linea retta, la forma della crescita lineare. In questa sezione, formalizzeremo un modo per descrivere la crescita lineare usando termini e concetti matematici. Alla fine di questa sezione, sarete in grado di scrivere sia un’equazione ricorsiva che esplicita per la crescita lineare date le condizioni di partenza, o una costante di cambiamento. Sarete anche in grado di riconoscere la differenza tra crescita lineare e geometrica dato un grafico o un’equazione.

Crescita lineare (algebrica)

Previsione della crescita

Marco è un collezionista di antiche bottiglie di soda. La sua collezione contiene attualmente 437 bottiglie. Ogni anno, mette a bilancio abbastanza soldi per comprare 32 nuove bottiglie. Possiamo determinare quante bottiglie avrà tra 5 anni e quanto tempo ci vorrà perché la sua collezione raggiunga le 1000 bottiglie?

Sebbene si possano probabilmente risolvere entrambe queste domande senza un’equazione o una matematica formale, formalizzeremo il nostro approccio a questo problema per fornire un mezzo per rispondere a domande più complicate.

Supponiamo che Pn rappresenti il numero, o popolazione, di bottiglie che Marco ha dopo n anni. Così P0 rappresenterebbe il numero di bottiglie ora, P1 rappresenterebbe il numero di bottiglie dopo 1 anno, P2 rappresenterebbe il numero di bottiglie dopo 2 anni, e così via. Potremmo descrivere come la collezione di bottiglie di Marco sta cambiando usando:

P0 = 437

Pn = Pn-1 + 32

Questa è chiamata una relazione ricorsiva. Una relazione ricorsiva è una formula che mette in relazione il prossimo valore in una sequenza con i valori precedenti. Qui, il numero di bottiglie nell’anno n può essere trovato aggiungendo 32 al numero di bottiglie dell’anno precedente, Pn-1. Usando questa relazione, potremmo calcolare:

P1 = P0 + 32 = 437 + 32 = 469

P2 = P1 + 32 = 469 + 32 = 501

P3 = P2 + 32 = 501 + 32 = 533

P4 = P3 + 32 = 533 + 32 = 565

P5 = P4 + 32 = 565 + 32 = 597

Abbiamo risposto alla domanda su quante bottiglie avrà Marco tra 5 anni.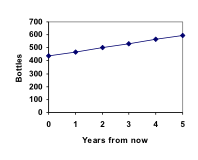

Tuttavia, risolvere quanto tempo ci vorrà perché la sua collezione raggiunga le 1000 bottiglie richiederebbe molti più calcoli.

Mentre le relazioni ricorsive sono eccellenti per descrivere in modo semplice e pulito come cambia una quantità, non sono convenienti per fare previsioni o risolvere problemi che si estendono nel futuro. Per questo, è preferibile una forma chiusa o esplicita per la relazione. Un’equazione esplicita ci permette di calcolare Pn direttamente, senza bisogno di conoscere Pn-1. Mentre potreste già essere in grado di indovinare l’equazione esplicita, ricaviamola dalla formula ricorsiva. Possiamo farlo selettivamente non semplificando man mano:

P1 = 437 + 32 = 437 + 1(32)

P2 = P1 + 32 = 437 + 32 + 32 = 437 + 2(32)

P3 = P2 + 32 = (437 + 2(32)) + 32 = 437 + 3(32)

P4 = P3 + 32 = (437 + 3(32)) + 32 = 437 + 4(32)

Ora probabilmente puoi vedere il modello, e generalizzare che

Pn = 437 + n(32) = 437 + 32n

Utilizzando questa equazione, possiamo calcolare quante bottiglie avrà dopo 5 anni:

P5 = 437 + 32(5) = 437 + 160 = 597

Possiamo ora risolvere anche quando la collezione raggiungerà 1000 bottiglie sostituendo 1000 per Pn e risolvendo n

1000 = 437 + 32n

563 = 32n

n = 563/32 = 17.59

Quindi Marco raggiungerà 1000 bottiglie in 18 anni.

I passi per determinare la formula e risolvere il problema della collezione di bottiglie di Marco sono spiegati in dettaglio nei video seguenti.

In questo esempio, la collezione di Marco è cresciuta dello stesso numero di bottiglie ogni anno. Questo cambiamento costante è la caratteristica che definisce la crescita lineare. Tracciando i valori che abbiamo calcolato per la collezione di Marco, possiamo vedere che i valori formano una linea retta, la forma della crescita lineare.

Crescita lineare

Se una quantità inizia alla dimensione P0 e cresce di d ogni periodo di tempo, allora la quantità dopo n periodi di tempo può essere determinata usando una di queste relazioni:

Forma ricorsiva

Pn = Pn-1 + d

Forma esplicita

Pn = P0 + d n

In questa equazione, d rappresenta la differenza comune – la quantità che la popolazione cambia ogni volta che n aumenta di 1.

Collegamento all’apprendimento precedente: Pendenza e intercetta

Potresti riconoscere la differenza comune, d, nella nostra equazione lineare come pendenza. Infatti, l’intera equazione esplicita dovrebbe sembrarti familiare – è la stessa equazione lineare che hai imparato in algebra, probabilmente dichiarata come y = mx + b.

Nell’equazione algebrica standard y = mx + b, b era l’intercetta y, o il valore y quando x era zero. Nella forma dell’equazione che stiamo usando, stiamo usando P0 per rappresentare quella quantità iniziale.

Nell’equazione y = mx + b, ricorda che m era la pendenza. Potreste ricordarlo come “salita su corsa”, o il cambiamento in y diviso per il cambiamento in x. In entrambi i casi, rappresenta la stessa cosa della differenza comune, d, che stiamo usando – la quantità che l’uscita Pn cambia quando l’ingresso n aumenta di 1.

Le equazioni y = mx + b e Pn = P0 + d n significano la stessa cosa e possono essere usate negli stessi modi. Le scriviamo solo in modo diverso.

Esempi

La popolazione di alci in una foresta nazionale è stata misurata a 12.000 nel 2003, ed è stata misurata di nuovo a 15.000 nel 2007. Se la popolazione continua a crescere linearmente a questo ritmo, quale sarà la popolazione di alci nel 2014?

Mostra la soluzione

Per iniziare, dobbiamo definire come misureremo n. Ricorda che P0 è la popolazione quando n = 0, quindi probabilmente non vogliamo usare letteralmente l’anno 0. Poiché conosciamo già la popolazione nel 2003, definiamo n = 0 come l’anno 2003.

Allora P0 = 12.000.

Poi dobbiamo trovare d. Ricordate che d è la crescita per periodo di tempo, in questo caso la crescita per anno. Tra le due misurazioni, la popolazione è cresciuta di 15.000-12.000 = 3.000, ma ci sono voluti 2007-2003 = 4 anni per crescere così tanto. Per trovare la crescita all’anno, possiamo dividere: 3000 alci / 4 anni = 750 alci in 1 anno.

In alternativa, si può usare la formula della pendenza dall’algebra per determinare la differenza comune, notando che la popolazione è l’output della formula, e il tempo è l’input.

d=pendenza=\frac{cambiamento in uscita}{cambiamento in entrata}}==frac{15.000-12.000}{2007-2003}=\frac{3000}{4}=750

Ora possiamo scrivere la nostra equazione nella forma che preferiamo.

Forma ricorsiva

P0 = 12.000

Pn = Pn-1 + 750

Forma esplicita

Pn = 12.000 + 750(n)

Per rispondere alla domanda, dobbiamo prima notare che l’anno 2014 sarà n = 11, poiché il 2014 è 11 anni dopo il 2003. La forma esplicita sarà più facile da usare per questo calcolo:

P11 = 12.000 + 750(11) = 20.250 alci

Vedi di più su questo esempio qui.

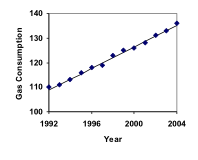
Il consumo di benzina negli USA è aumentato costantemente. I dati di consumo dal 1992 al 2004 sono mostrati qui sotto. Trova un modello per questi dati e usalo per prevedere il consumo nel 2016. Se la tendenza continua, quando il consumo raggiungerà i 200 miliardi di galloni?

Anno ’92 ’93 ’94 ’95 ’96 ’97 ’98 ’99 ’00 ’01 ’02 ’03 ’04
Consumo (miliardi di galloni) 110 111 113 116 118 119 123 125 126 128 131 133 136
Mostra soluzione

Tracciando questi dati, sembra avere una relazione approssimativamente lineare:

Mentre ci sono tecniche statistiche più avanzate che possono essere usate per trovare un’equazione per modellare i dati, per avere un’idea di quello che sta succedendo, possiamo trovare un’equazione usando due parti dei dati – forse i dati del 1993 e del 2003.

Facendo corrispondere n = 0 al 1993 si otterrebbe P0 = 111 miliardi di galloni.

Per trovare d, dobbiamo sapere quanto è aumentato il consumo di gas ogni anno, in media. Dal 1993 al 2003 il consumo di gas è aumentato da 111 miliardi di galloni a 133 miliardi di galloni, un cambiamento totale di 133 – 111 = 22 miliardi di galloni, in 10 anni. Questo ci dà un cambiamento medio di 22 miliardi di galloni / 10 anni = 2,2 miliardi di galloni all’anno.

Equivalentemente,

d=slope=\frac{cambiamento in uscita}{cambiamento in entrata}}=\frac{133-111}{10-0}=\frac{22}{10}=2.2 miliardi di galloni all’anno

Possiamo ora scrivere la nostra equazione nella forma preferita.

Forma ricorsiva

P0 = 111

Pn = Pn-1 + 2.2

Forma esplicita

Pn = 111 + 2.2n

Calcolare i valori usando la forma esplicita e tracciarli con i dati originali mostra quanto bene il nostro modello si adatti ai dati.

Possiamo ora usare il nostro modello per fare previsioni sul futuro, assumendo che la tendenza precedente continui immutata. Per prevedere il consumo di benzina nel 2016:

n = 23 (2016 – 1993 = 23 anni dopo)

P23 = 111 + 2,2(23) = 161,6

Il nostro modello prevede che gli USA consumeranno 161.6 miliardi di galloni di benzina nel 2016 se la tendenza attuale continua.

Per trovare quando il consumo raggiungerà i 200 miliardi di galloni, dobbiamo impostare Pn = 200, e risolvere per n:

Pn = 200 Sostituire Pn con il nostro modello

111 + 2.2n = 200 Sottrarre 111 da entrambi i lati

2.2n = 89 Dividere entrambi i lati per 2.2

n = 40.4545

Questo ci dice che il consumo raggiungerà 200 miliardi circa 40 anni dopo il 1993, che sarebbe nell’anno 2033.

I passi per raggiungere questa risposta sono dettagliati nel seguente video.

Il costo, in dollari, di un abbonamento in palestra per n mesi può essere descritto dall’equazione esplicita Pn = 70 + 30n. Cosa ci dice questa equazione?

Mostra la soluzione

Il valore di P0 in questa equazione è 70, quindi il costo iniziale è 70 dollari. Questo ci dice che ci deve essere una tassa di iniziazione o di avvio di 70 dollari per iscriversi alla palestra.

Il valore di d nell’equazione è 30, quindi il costo aumenta di 30 dollari ogni mese. Questo ci dice che la quota mensile di iscrizione alla palestra è di 30 dollari al mese.

La spiegazione di questo esempio è dettagliata qui sotto.

Prova

Il numero di padri casalinghi in Canada è in costante crescita. Mentre la tendenza non è perfettamente lineare, è abbastanza lineare. Usa i dati del 1976 e del 2010 per trovare una formula esplicita per il numero di padri casalinghi, poi usala per prevedere il numero nel 2020.

Anno 1976 1984 1991 2000 2010
# di padri casalinghihome fathers 20610 28725 43530 47665 53555
Show Solution

Letting n= 0 correspond with 1976, allora P_0= 20.610.
Dal 1976 al 2010 il numero di padri casalinghi è aumentato di 53.555 – 20.610 = 32.945
Questo è successo in 34 anni, dando un comune diverso d di 32.945 / 34 = 969.
P_n= 20.610 + 969n
Prevedendo per il 2020, usiamo n = 44, P(44) = 20.610 + 969(44) = 63.246 padri casalinghi nel 2020.

Quando i buoni modelli vanno male

Quando si usano modelli matematici per prevedere il comportamento futuro, è importante tenere a mente che pochissime tendenze continueranno all’infinito.

Esempio

Supponiamo che un bambino di quattro anni sia attualmente alto 39 pollici, e ci venga detto di aspettarci che cresca di 2,5 pollici l’anno.

Possiamo impostare un modello di crescita, con n = 0 corrispondente a 4 anni.

Forma ricorsiva

P0 = 39

Pn = Pn-1 + 2,5

Forma esplicita

Pn = 39 + 2.5(n)

Così a 6 anni, ci aspetteremmo che fosse

P2 = 39 + 2,5(2) = 44 pollici di altezza

Qualunque modello matematico alla fine si rompe. Certamente, non dovremmo aspettarci che questo ragazzo continui a crescere allo stesso ritmo per tutta la vita. Se lo facesse, all’età di 50 anni sarebbe

P46 = 39 + 2,5(46) = 154 pollici di altezza = 12,8 piedi di altezza!

Quando usiamo qualsiasi modello matematico, dobbiamo considerare quali input sono ragionevoli da usare. Ogni volta che estrapoliamo, o facciamo previsioni nel futuro, stiamo assumendo che il modello continuerà ad essere valido.

Vedi una spiegazione video di questa scomposizione del modello di crescita lineare qui.

Crescita esponenziale (geometrica)

Crescita della popolazione

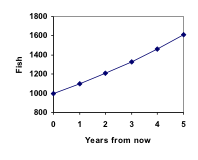
Supponiamo che ogni anno, solo il 10% dei pesci in un lago abbia prole superstite. Se l’anno scorso c’erano 100 pesci nel lago, ora ce ne sarebbero 110. Se l’anno scorso c’erano 1000 pesci nel lago, ora ce ne sarebbero 1100. In assenza di fattori inibitori, le popolazioni di persone e animali tendono a crescere di una percentuale della popolazione esistente ogni anno.


Supponiamo che il nostro lago abbia iniziato con 1000 pesci, e che il 10% dei pesci abbia prole superstite ogni anno. Poiché iniziamo con 1000 pesci, P0 = 1000. Come calcoliamo P1? La nuova popolazione sarà la vecchia popolazione, più un ulteriore 10%. Simbolicamente:

P1 = P0 + 0,10P0

Nota che questo potrebbe essere condensato in una forma più breve tramite la fattorizzazione:

P1 = P0 + 0,10P0 = 1P0 + 0,10P0 = (1+ 0,10)P0 = 1,10P0

Mentre il 10% è il tasso di crescita, 1,10 è il moltiplicatore della crescita. Notate che 1,10 può essere pensato come “il 100% originale più un 10% aggiuntivo”

Per la nostra popolazione di pesci,

P1 = 1,10(1000) = 1100

Possiamo quindi calcolare la popolazione negli anni successivi:

P2 = 1,10P1 = 1,10(1100) = 1210

P3 = 1,10P2 = 1,10(1210) = 1331

Nota che nel primo anno la popolazione è cresciuta di 100 pesci; nel secondo anno la popolazione è cresciuta di 110 pesci; e nel terzo anno la popolazione è cresciuta di 121 pesci.

Mentre c’è una crescita percentuale costante, l’aumento effettivo del numero di pesci aumenta ogni anno.

Grafando questi valori vediamo che questa crescita non appare del tutto lineare.

Un walkthrough di questo scenario di pesci può essere visto qui:

Per avere un quadro migliore di come questa crescita basata sulla percentuale influenzi le cose, abbiamo bisogno di una forma esplicita, così possiamo calcolare rapidamente i valori più avanti nel futuro.

Come abbiamo fatto per il modello lineare, inizieremo a costruire dall’equazione ricorsiva:

P1 = 1.10(P0 )= 1.10(1000)

P2 = 1.10(P1 )= 1.10(1.10(1000)) = 1.102(1000)

P3 = 1.10(P2 )= 1.10(1.102(1000)) = 1.103(1000)

P4 = 1.10(P3 )= 1.10(1.103(1000)) = 1.104(1000)

Osservando un modello, possiamo generalizzare la forma esplicita per essere:

Pn = 1.10n(1000), o equivalentemente, Pn = 1000(1.10n)

Da questo, possiamo calcolare rapidamente il numero di pesci in 10, 20, o 30 anni:

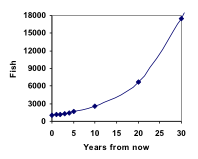
P10 = 1.1010(1000) = 2594

P20 = 1.1020(1000) = 6727

P30 = 1.1030(1000) = 17449

Aggiungendo questi valori al nostro grafico si nota una forma decisamente non lineare. Se la nostra popolazione di pesci fosse cresciuta linearmente, di 100 pesci ogni anno, la popolazione avrebbe raggiunto solo 4000 in 30 anni, rispetto a quasi 18.000 con questa crescita basata sulla percentuale, chiamata crescita esponenziale.

Un video che dimostra il modello esplicito di questa storia di pesci può essere visto qui:

Nella crescita esponenziale, la popolazione cresce proporzionalmente alla dimensione della popolazione, così come la popolazione diventa più grande, la stessa crescita percentuale darà una crescita numerica maggiore.

Crescita esponenziale

Se una quantità inizia dalla dimensione P0 e cresce del R% (scritto come decimale, r) ogni periodo di tempo, allora la quantità dopo n periodi di tempo può essere determinata usando una di queste relazioni:

Forma ricorsiva

Pn = (1+r) Pn-1

Forma esplicita

Pn = (1+r)n P0 o equivalentemente, Pn = P0 (1+r)n

Chiamo r il tasso di crescita.

Il termine (1+r) è chiamato moltiplicatore di crescita, o rapporto comune.

Esempio

Tra il 2007 e il 2008, Olympia, WA è cresciuta quasi del 3% fino a una popolazione di 245 mila persone. Se questo tasso di crescita dovesse continuare, quale sarebbe la popolazione di Olympia nel 2014?

Mostra la soluzione

Come abbiamo fatto prima, dobbiamo prima definire quale anno corrisponderà a n = 0. Poiché conosciamo la popolazione nel 2008, avrebbe senso far corrispondere il 2008 a n = 0, quindi P0 = 245.000. L’anno 2014 sarebbe quindi n = 6.

Sappiamo che il tasso di crescita è del 3%, dando r = 0,03.

Utilizzando la forma esplicita:

P6 = (1+0,03)6 (245.000) = 1,19405(245.000) = 292.542,25

Il modello prevede che nel 2014, Olympia avrebbe una popolazione di circa 293 mila persone.

Il seguente video spiega questo esempio in dettaglio.

Valutare gli esponenti sulla calcolatrice

Per valutare espressioni come (1,03)6, sarà più facile usare una calcolatrice che moltiplicare 1,03 per se stesso sei volte. La maggior parte delle calcolatrici scientifiche hanno un pulsante per gli esponenti. Di solito è etichettato come:

^ , yx, o xy .

Per valutare 1,036 dovremmo digitare 1,03 ^ 6, o 1,03 yx 6. Prova – dovresti ottenere una risposta intorno a 1,1940523.

Prova

L’India è il secondo paese più popoloso del mondo, con una popolazione nel 2008 di circa 1,14 miliardi di persone. La popolazione cresce di circa l’1,34% ogni anno. Se questa tendenza continua, a quanto crescerà la popolazione dell’India entro il 2020?

Mostra la soluzione

Utilizzando n = 0 corrispondente al 2008, P_12= (1+0,0134)12(1,14) = circa 1.337 miliardi di persone nel 2020

Esempi

Un amico sta usando l’equazione Pn = 4600(1.072)n per prevedere la retta annuale di un college locale. Dice che la formula si basa sugli anni successivi al 2010. Cosa ci dice questa equazione?

Mostra la soluzione

Nell’equazione, P0 = 4600, che è il valore iniziale della retta quando n = 0. Questo ci dice che la retta nel 2010 era di $4,600.

Il moltiplicatore di crescita è 1,072, quindi il tasso di crescita è 0,072, o 7,2%. Questo ci dice che ci si aspetta che la retta cresca del 7,2% ogni anno.

Insieme, potremmo dire che la retta nel 2010 era di 4.600 dollari, e ci si aspetta che cresca del 7,2% ogni anno.

Vedi quanto segue per vedere questo esempio elaborato.

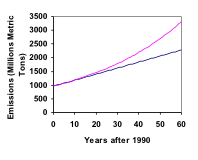
Nel 1990, l’uso di energia residenziale negli USA era responsabile di 962 milioni di tonnellate metriche di emissioni di anidride carbonica. Nel 2000, questo numero era salito a 1182 milioni di tonnellate. Se le emissioni crescono esponenzialmente e continuano allo stesso ritmo, a quanto cresceranno le emissioni entro il 2050?

Mostra la soluzione

Come in precedenza, faremo corrispondere n = 0 con il 1990, poiché questo è l’anno del primo dato che abbiamo. Questo farà sì che P0 = 962 (milioni di tonnellate di CO2). In questo problema, non ci viene dato il tasso di crescita, ma ci viene dato che P10 = 1182.

Quando n = 10, l’equazione esplicita appare come:

P10 = (1+r)10 P0

Conosciamo il valore di P0, quindi possiamo inserirlo nell’equazione:

P10 = (1+r)10 962

Sappiamo anche che P10 = 1182, quindi sostituendolo, otteniamo

1182 = (1+r)10 962

Ora possiamo risolvere questa equazione per il tasso di crescita, r. Iniziare dividendo per 962.

frac{1182}{962}={(1+r)}^{10} Prendi la decima radice di entrambi i lati

\sqrt{frac{1182}{962}=1+r Sottrai 1 da entrambi i lati

r=\sqrt{frac{1182}{962}-1=0,0208 = 2,08%

Quindi se le emissioni stanno crescendo esponenzialmente, stanno crescendo di circa 2,08% all’anno. Possiamo ora prevedere le emissioni nel 2050 trovando P60

P60 = (1+0,0208)60 962 = 3308,4 milioni di tonnellate di CO2 nel 2050

Vedi di più su questo esempio qui.

Arrotondamento

Come nota sull’arrotondamento, notate che se avessimo arrotondato il tasso di crescita al 2,1%, il nostro calcolo per le emissioni nel 2050 sarebbe stato 3347. L’arrotondamento al 2% avrebbe cambiato il nostro risultato in 3156. Una differenza molto piccola nei tassi di crescita viene ingrandita molto nella crescita esponenziale. Per questo motivo, si raccomanda di arrotondare il tasso di crescita il meno possibile.

Se avete bisogno di arrotondare, mantenete almeno tre cifre significative – i numeri dopo qualsiasi zero iniziale. Così 0,4162 potrebbe essere ragionevolmente arrotondato a 0,416. Un tasso di crescita di 0,001027 potrebbe essere ragionevolmente arrotondato a 0,00103.

Valutazione delle radici sulla calcolatrice

Nell’esempio precedente, abbiamo dovuto calcolare la decima radice di un numero. Questo è diverso dal prendere la radice quadrata di base, √. Molte calcolatrici scientifiche hanno un pulsante per le radici generali. È tipicamente etichettato come:

\sqrt{x}

Per valutare la terza radice di 8, per esempio, dovremmo digitare 3 \sqrt{{}} 8, o 8 \sqrt{{{}} 3, a seconda della calcolatrice. Prova sulla tua per vedere quale usare – dovresti ottenere una risposta di 2.

Se la tua calcolatrice non ha un pulsante per la radice generale, non tutto è perduto. Potete invece usare la proprietà degli esponenti che afferma che:

\sqrt{a}={a}^{frac{1}{2}}.

Quindi, per calcolare la terza radice di 8, potete usare il tasto esponente della vostra calcolatrice per valutare 81/3. Per fare questo, digitate:

8 yx ( 1 ÷ 3 )

Le parentesi dicono alla calcolatrice di dividere 1/3 prima di fare l’esponente.

Prova

Il numero di utenti su un sito di social networking era di 45 mila a febbraio quando è diventato ufficialmente pubblico, ed è cresciuto a 60 mila entro ottobre. Se il sito sta crescendo esponenzialmente, e la crescita continua allo stesso ritmo, quanti utenti dovrebbero aspettarsi due anni dopo la pubblicazione?

Mostra la soluzione

Qui misureremo n in mesi piuttosto che in anni, con n = 0 corrispondente a febbraio quando è stato pubblicato. Questo dà P_0= 45 mila. Ottobre è 8 mesi dopo, quindi P_8= 60.
P_8=(1+r)^{8}P_0
60=(1+r)^{8}45
\frac{60}{45}=(1+r)^8
\sqrt{frac{60}{45}=1+r
r=\sqrt{frac{60}{45}-1=0.0366\text{ o }3.66%
L’equazione generale esplicita è P_n =(1.0366)^{n}45. Prevedendo 24 mesi dopo la loro pubblicazione si ottiene P_{24}=(1.0366)^{24}45=106.63 mila utenti.

Esempio

Ritornando all’ultimo esempio, per fare un confronto, quali sarebbero le emissioni di carbonio nel 2050 se le emissioni crescessero linearmente allo stesso ritmo?

Mostra la soluzione

Ancora una volta avremo n = 0 corrispondente al 1990, dando P0 = 962. Per trovare d, potremmo adottare lo stesso approccio di prima, notando che le emissioni sono aumentate di 220 milioni di tonnellate metriche in 10 anni, dando una differenza comune di 22 milioni di tonnellate metriche ogni anno.

In alternativa, potremmo usare un approccio simile a quello che abbiamo usato per trovare l’equazione esponenziale. Quando n = 10, l’equazione lineare esplicita appare come:

P10 = P0 + 10d

Conosciamo il valore di P0, quindi possiamo inserirlo nell’equazione:

P10 = 962 + 10d

Siccome sappiamo che P10 = 1182, sostituendolo otteniamo

1182 = 962 + 10d

Ora possiamo risolvere questa equazione per la differenza comune, d.

1182 – 962 = 10d

220 = 10d

d = 22

Questo ci dice che se le emissioni stanno cambiando linearmente, stanno crescendo di 22 milioni di tonnellate ogni anno. Prevedendo le emissioni nel 2050,

P60 = 962 + 22(60) = 2282 milioni di tonnellate.

Si noterà che questo numero è sostanzialmente inferiore alla previsione del modello di crescita esponenziale. Calcolare e tracciare più valori aiuta a illustrare le differenze.

Una dimostrazione di questo esempio può essere vista nel seguente video.

Come possiamo sapere quale modello di crescita usare quando lavoriamo con i dati? Ci sono due approcci che dovrebbero essere usati insieme quando possibile:

  1. Trova più di due pezzi di dati. Traccia i valori e cerca una tendenza. I dati sembrano cambiare come una linea, o i valori sembrano curvare verso l’alto?
  2. Considera i fattori che contribuiscono ai dati. Sono cose che ci si aspetta cambino linearmente o esponenzialmente? Per esempio, nel caso delle emissioni di carbonio, potremmo aspettarci che, in assenza di altri fattori, esse siano strettamente legate ai valori della popolazione, che tendono a cambiare esponenzialmente.

By: adminPosted on

Lascia un commento

Il tuo indirizzo email non sarà pubblicato.