Mathématiques pour les arts libéraux

Avoir un taux de changement constant est la caractéristique déterminante de la croissance linéaire. Le tracé des paires de coordonnées associées à un changement constant donnera une ligne droite, la forme de la croissance linéaire. Dans cette section, nous allons formaliser une façon de décrire la croissance linéaire en utilisant des termes et des concepts mathématiques. À la fin de cette section, vous serez en mesure d’écrire des équations récursives et explicites pour la croissance linéaire en fonction des conditions de départ ou d’une constante de changement. Vous serez également capable de reconnaître la différence entre une croissance linéaire et géométrique étant donné un graphique ou une équation.

Croissance linéaire (algébrique)

Prédire la croissance

Marco est un collectionneur de bouteilles de soda anciennes. Sa collection compte actuellement 437 bouteilles. Chaque année, il budgétise suffisamment d’argent pour acheter 32 nouvelles bouteilles. Peut-on déterminer combien de bouteilles il aura dans 5 ans, et combien de temps il faudra pour que sa collection atteigne 1000 bouteilles ?

Bien que vous puissiez probablement résoudre ces deux questions sans équation ou sans mathématiques formelles, nous allons formaliser notre approche de ce problème pour fournir un moyen de répondre à des questions plus compliquées.

Supposons que Pn représente le nombre, ou la population, de bouteilles que Marco possède après n années. Donc P0 représenterait le nombre de bouteilles maintenant, P1 représenterait le nombre de bouteilles après 1 an, P2 représenterait le nombre de bouteilles après 2 ans, et ainsi de suite. Nous pourrions décrire comment la collection de bouteilles de Marco évolue en utilisant :

P0 = 437

Pn = Pn-1 + 32

C’est ce qu’on appelle une relation récursive. Une relation récursive est une formule qui relie la valeur suivante d’une séquence aux valeurs précédentes. Ici, on peut trouver le nombre de bouteilles de l’année n en ajoutant 32 au nombre de bouteilles de l’année précédente, Pn-1. En utilisant cette relation, nous pourrions calculer :

P1 = P0 + 32 = 437 + 32 = 469

P2 = P1 + 32 = 469 + 32 = 501

P3 = P2 + 32 = 501 + 32 = 533

P4 = P3 + 32 = 533 + 32 = 565

P5 = P4 + 32 = 565 + 32 = 597

Nous avons répondu à la question de savoir combien de bouteilles Marco aura dans 5 ans.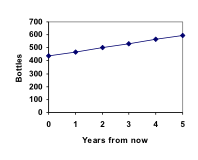

Cependant, résoudre le temps qu’il faudra pour que sa collection atteigne 1000 bouteilles nécessiterait beaucoup plus de calculs.

Bien que les relations récursives soient excellentes pour décrire simplement et proprement comment une quantité évolue, elles ne sont pas pratiques pour faire des prédictions ou résoudre des problèmes qui s’étendent loin dans le futur. Pour cela, une forme fermée ou explicite de la relation est préférable. Une équation explicite nous permet de calculer directement Pn, sans avoir besoin de connaître Pn-1. Bien que vous puissiez déjà deviner l’équation explicite, dérivons-la de la formule récursive. Nous pouvons le faire en ne simplifiant pas sélectivement au fur et à mesure :

P1 = 437 + 32 = 437 + 1(32)

P2 = P1 + 32 = 437 + 32 + 32 = 437 + 2(32)

P3 = P2 + 32 = (437 + 2(32)) + 32 = 437 + 3(32)

P4 = P3 + 32 = (437 + 3(32)) + 32 = 437 + 4(32)

Vous pouvez probablement voir le modèle maintenant, et généraliser que

Pn = 437 + n(32) = 437 + 32n

En utilisant cette équation, nous pouvons calculer combien de bouteilles il aura après 5 ans :

P5 = 437 + 32(5) = 437 + 160 = 597

Nous pouvons maintenant aussi résoudre le moment où la collection atteindra 1000 bouteilles en substituant 1000 pour Pn et en résolvant pour n

1000 = 437 + 32n

563 = 32n

n = 563/32 = 17.59

Donc Marco atteindra 1000 bouteilles dans 18 ans.

Les étapes de détermination de la formule et de résolution du problème de la collection de bouteilles de Marco sont expliquées en détail dans les vidéos suivantes.

Dans cet exemple, la collection de Marco a augmenté du même nombre de bouteilles chaque année. Ce changement constant est la caractéristique déterminante de la croissance linéaire. En traçant les valeurs que nous avons calculées pour la collection de Marco, nous pouvons voir que les valeurs forment une ligne droite, la forme de la croissance linéaire.

Exemples

La population de wapitis dans une forêt nationale a été mesurée à 12 000 en 2003, et a été mesurée à nouveau à 15 000 en 2007. Si la population continue de croître linéairement à ce rythme, quelle sera la population d’élans en 2014 ?

Afficher la solution

Pour commencer, nous devons définir comment nous allons mesurer n. Rappelez-vous que P0 est la population lorsque n = 0, donc nous ne voulons probablement pas utiliser littéralement l’année 0. Puisque nous connaissons déjà la population en 2003, définissons n = 0 comme étant l’année 2003.

Alors P0 = 12 000.

Puis nous devons trouver d. Rappelez-vous que d est la croissance par période de temps, dans ce cas la croissance par année. Entre les deux mesures, la population a augmenté de 15 000-12 000 = 3 000, mais il a fallu 2007-2003 = 4 ans pour augmenter autant. Pour trouver la croissance par an, nous pouvons diviser : 3000 wapitis / 4 ans = 750 wapitis en 1 an.

Alternativement, vous pouvez utiliser la formule de pente de l’algèbre pour déterminer la différence commune, en notant que la population est la sortie de la formule, et le temps est l’entrée.

d=slope=\frac{\text{changement en sortie}{\text{changement en entrée}}=\frac{15 000-12 000}{2007-2003}=\frac{3000}{4}=750

Nous pouvons maintenant écrire notre équation sous la forme que vous préférez.

Forme récursive

P0 = 12 000

Pn = Pn-1 + 750

Forme explicite

Pn = 12 000 + 750(n)

Pour répondre à la question, nous devons d’abord noter que l’année 2014 sera n = 11, puisque 2014 est 11 ans après 2003. La forme explicite sera plus facile à utiliser pour ce calcul :

P11 = 12 000 + 750(11) = 20 250 wapitis

Voir plus sur cet exemple ici.

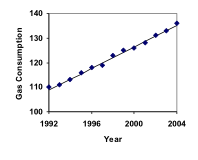
La consommation d’essence aux États-Unis a augmenté régulièrement. Les données de consommation de 1992 à 2004 sont présentées ci-dessous. Trouvez un modèle pour ces données, et utilisez-le pour prédire la consommation en 2016. Si la tendance se poursuit, quand la consommation atteindra-t-elle 200 milliards de gallons ?

Année	’92	’93	’94	’95	’96	’97	’98	’99	’00	’01	’02	’03	’04
Consommation (milliards de gallons)	110	111	113	116	118	119	123	125	126	128	131	133	136

Afficher la solution

Placer ces données, il semble y avoir une relation approximativement linéaire :

Bien qu’il existe des techniques statistiques plus avancées qui peuvent être utilisées pour trouver une équation pour modéliser les données, pour avoir une idée de ce qui se passe, nous pouvons trouver une équation en utilisant deux morceaux de données – peut-être les données de 1993 et 2003.

Laisser n = 0 correspondre à 1993 donnerait P0 = 111 milliards de gallons.

Pour trouver d, nous devons savoir de combien la consommation de gaz a augmenté chaque année, en moyenne. De 1993 à 2003, la consommation de gaz est passée de 111 milliards de gallons à 133 milliards de gallons, soit une variation totale de 133 – 111 = 22 milliards de gallons, sur 10 ans. Cela nous donne une variation moyenne de 22 milliards de gallons / 10 ans = 2,2 milliards de gallons par an.

Equivalemment,

d=slope=\frac{\text{changeinoutput}}{\text{changeinput}}=\frac{133-111}{10-0}=\frac{22}{10}=2.2billion gallons per year

Nous pouvons maintenant écrire notre équation sous la forme que vous préférez.

Forme récursive

P0 = 111

Pn = Pn-1 + 2.2

Forme explicite

Pn = 111 + 2,2n

Calculer des valeurs en utilisant la forme explicite et les tracer avec les données originales montre à quel point notre modèle s’adapte aux données.

Nous pouvons maintenant utiliser notre modèle pour faire des prédictions sur l’avenir, en supposant que la tendance précédente reste inchangée. Pour prédire la consommation d’essence en 2016 :

n = 23 (2016 – 1993 = 23 ans plus tard)

P23 = 111 + 2,2(23) = 161,6

Notre modèle prédit que les États-Unis consommeront 161.6 milliards de gallons d’essence en 2016 si la tendance actuelle se poursuit.

Pour trouver quand la consommation atteindra 200 milliards de gallons, nous fixerions Pn = 200, et résoudrions pour n :

Pn = 200 Remplacer Pn par notre modèle

111 + 2.2n = 200 Soustraire 111 des deux côtés

2,2n = 89 Diviser les deux côtés par 2,2

n = 40,4545

Cela nous indique que la consommation atteindra 200 milliards environ 40 ans après 1993, ce qui serait en 2033.

Les étapes pour arriver à cette réponse sont détaillées dans la vidéo suivante.

Le coût, en dollars, d’un abonnement à une salle de sport pendant n mois peut être décrit par l’équation explicite Pn = 70 + 30n. Qu’est-ce que cette équation nous apprend ?

Montrer la solution

La valeur de P0 dans cette équation est 70, donc le coût initial de départ est de 70 $. Cela nous indique qu’il doit y avoir des frais d’initiation ou de démarrage de 70 $ pour s’inscrire à la salle de sport.

La valeur de d dans l’équation est 30, donc le coût augmente de 30 $ chaque mois. Cela nous indique que les frais mensuels d’adhésion à la salle de sport sont de 30 $ par mois.

L’explication de cet exemple est détaillée ci-dessous.

Quand les bons modèles tournent mal

Lorsqu’on utilise des modèles mathématiques pour prédire un comportement futur, il est important de garder à l’esprit que très peu de tendances se poursuivront indéfiniment.

Croissance exponentielle (géométrique )

Croissance de la population

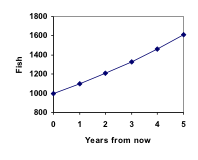
Supposons que chaque année, seulement 10% des poissons dans un lac ont une progéniture survivante. S’il y avait 100 poissons dans le lac l’année dernière, il y aurait maintenant 110 poissons. S’il y avait 1000 poissons dans le lac l’année dernière, il y aurait maintenant 1100 poissons. En l’absence de tout facteur inhibiteur, les populations de personnes et d’animaux ont tendance à augmenter d’un pourcentage de la population existante chaque année.

Supposons que notre lac ait commencé avec 1000 poissons, et que 10% des poissons aient une progéniture survivante chaque année. Puisque nous commençons avec 1000 poissons, P0 = 1000. Comment calculer P1 ? La nouvelle population sera l’ancienne population, plus 10% supplémentaires. Symboliquement:

P1 = P0 + 0,10P0

Notez que cela pourrait être condensé sous une forme plus courte en factorisant:

P1 = P0 + 0,10P0 = 1P0 + 0,10P0 = (1+ 0,10)P0 = 1,10P0

Alors que 10% est le taux de croissance, 1,10 est le multiplicateur de croissance. Remarquez que 1,10 peut être considéré comme « les 100% initiaux plus 10% supplémentaires »

Pour notre population de poissons,

P1 = 1,10(1000) = 1100

Nous pourrions alors calculer la population dans les années ultérieures :

P2 = 1,10P1 = 1,10(1100) = 1210

P3 = 1,10P2 = 1,10(1210) = 1331

Notez que la première année, la population a augmenté de 100 poissons ; la deuxième année, la population a augmenté de 110 poissons ; et la troisième année, la population a augmenté de 121 poissons.

Bien qu’il y ait une croissance constante en pourcentage, l’augmentation réelle du nombre de poissons augmente chaque année.

En graphant ces valeurs, nous voyons que cette croissance n’apparaît pas tout à fait linéaire.

Un walkthrough de ce scénario de poissons peut être visualisé ici :

Pour avoir une meilleure image de la façon dont cette croissance en pourcentage affecte les choses, nous avons besoin d’une forme explicite, afin de pouvoir calculer rapidement les valeurs plus loin dans le futur.

Comme nous l’avons fait pour le modèle linéaire, nous allons commencer à construire à partir de l’équation récursive :

P1 = 1,10(P0 )= 1,10(1000)

P2 = 1,10(P1 )= 1,10(1,10(1000)) = 1,102(1000)

P3 = 1.10(P2 )= 1.10(1.102(1000)) = 1.103(1000)

P4 = 1.10(P3 )= 1.10(1.103(1000)) = 1.104(1000)

Observant un modèle, nous pouvons généraliser la forme explicite pour être:

Pn = 1.10n(1000), ou de manière équivalente, Pn = 1000(1.10n)

À partir de là, nous pouvons rapidement calculer le nombre de poissons dans 10, 20 ou 30 ans :

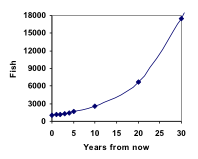
P10 = 1.1010(1000) = 2594

P20 = 1.1020(1000) = 6727

P30 = 1.1030(1000) = 17449

L’ajout de ces valeurs à notre graphique révèle une forme qui n’est définitivement pas linéaire. Si notre population de poissons avait augmenté linéairement, de 100 poissons chaque année, la population n’aurait atteint que 4000 en 30 ans, contre près de 18 000 avec cette croissance basée sur le pourcentage, appelée croissance exponentielle.

Une vidéo démontrant le modèle explicite de cette histoire de poissons peut être visionnée ici :

Dans la croissance exponentielle, la population croît proportionnellement à la taille de la population, donc plus la population est grande, le même pourcentage de croissance donnera une croissance numérique plus grande.

Exemple

Entre 2007 et 2008, Olympia, WA a augmenté de près de 3% pour atteindre une population de 245 mille personnes. Si ce taux de croissance devait se poursuivre, quelle serait la population d’Olympia en 2014 ?

Montrer la solution

Comme nous l’avons fait précédemment, nous devons d’abord définir quelle année correspondra à n = 0. Puisque nous connaissons la population en 2008, il serait logique que 2008 corresponde à n = 0, donc P0 = 245 000. L’année 2014 serait alors n = 6.

Nous savons que le taux de croissance est de 3%, ce qui donne r = 0,03.

En utilisant la forme explicite :

P6 = (1+0,03)6 (245 000) = 1,19405(245 000) = 292 542,25

Le modèle prédit qu’en 2014, Olympie aurait une population d’environ 293 mille personnes.

La vidéo suivante explique cet exemple en détail.

Evaluation des exposants à la calculatrice

Pour évaluer des expressions comme (1,03)6, il sera plus facile d’utiliser une calculatrice que de multiplier six fois 1,03 par lui-même. La plupart des calculatrices scientifiques ont un bouton pour les exposants. Il est généralement étiqueté comme :

^ , yx , ou xy .

Pour évaluer 1,036, nous taperions 1,03 ^ 6, ou 1,03 yx 6. Essayez-le – vous devriez obtenir une réponse autour de 1,1940523.

Essayez-le

L’Inde est le deuxième pays le plus peuplé du monde, avec une population en 2008 d’environ 1,14 milliard de personnes. La population augmente d’environ 1,34% chaque année. Si cette tendance se poursuit, à combien s’élèvera la population de l’Inde en 2020 ?

Montrer la solution

En utilisant n = 0 correspondant à 2008, P_12= (1+0,0134)12(1,14) = environ 1.337 milliards de personnes en 2020

Exemples

Une amie utilise l’équation Pn = 4600(1,072)n pour prédire les frais de scolarité annuels d’une université locale. Elle dit que la formule est basée sur les années après 2010. Que nous apprend cette équation ?

Montrer la solution

Dans l’équation, P0 = 4600, qui est la valeur de départ des frais de scolarité lorsque n = 0. Cela nous indique que les frais de scolarité en 2010 étaient de 4 600 $.

Le multiplicateur de croissance est de 1,072, donc le taux de croissance est de 0,072, soit 7,2 %. Cela nous indique que les frais de scolarité devraient augmenter de 7,2 % chaque année.

En mettant tout cela ensemble, nous pourrions dire que les frais de scolarité en 2010 étaient de 4 600 $, et qu’ils devraient augmenter de 7,2 % chaque année.

Voyez ce qui suit pour voir cet exemple travaillé.

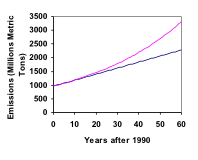
En 1990, la consommation d’énergie résidentielle aux États-Unis était responsable de 962 millions de tonnes métriques d’émissions de dioxyde de carbone. En l’an 2000, ce chiffre était passé à 1182 millions de tonnes métriques. Si les émissions augmentent de façon exponentielle et continuent au même rythme, à combien s’élèveront-elles en 2050 ?

Montrer la solution

Comme précédemment, nous ferons correspondre n = 0 à 1990, car c’est l’année de la première donnée dont nous disposons. Cela donnera P0 = 962 (millions de tonnes métriques de CO2). Dans ce problème, on ne nous donne pas le taux de croissance, mais on nous indique plutôt que P10 = 1182.

Lorsque n = 10, l’équation explicite ressemble à :

P10 = (1+r)10 P0

Nous connaissons la valeur de P0, nous pouvons donc la mettre dans l’équation :

P10 = (1+r)10 962

Nous savons également que P10 = 1182, donc en le substituant, nous obtenons

1182 = (1+r)10 962

Nous pouvons maintenant résoudre cette équation pour le taux de croissance, r. Commencez par diviser par 962.

\frac{1182}{962}={{(1+r)}^{10}} Prenez la racine 10 des deux côtés

\sqrt{\frac{1182}{962}}=1+r Soustrayez 1 des deux côtés

r=\sqrt{\frac{1182}{962}}-1=0,0208 = 2,08%

Donc, si les émissions augmentent de façon exponentielle, elles augmentent d’environ 2,08% par an. Nous pouvons maintenant prédire les émissions en 2050 en trouvant P60

P60 = (1+0,0208)60 962 = 3308,4 millions de tonnes métriques de CO2 en 2050

Voir plus sur cet exemple ici.

Arrondi

En guise de remarque sur l’arrondi, remarquez que si nous avions arrondi le taux de croissance à 2,1%, notre calcul pour les émissions en 2050 aurait été de 3347. L’arrondi à 2% aurait changé notre résultat à 3156. Une très petite différence dans les taux de croissance est fortement amplifiée par la croissance exponentielle. Pour cette raison, il est recommandé d’arrondir le taux de croissance le moins possible.

Si vous devez arrondir, gardez au moins trois chiffres significatifs – les chiffres après tout zéros de tête. Ainsi, 0,4162 pourrait être raisonnablement arrondi à 0,416. Un taux de croissance de 0,001027 pourrait être raisonnablement arrondi à 0,00103.

Evaluation des racines sur la calculatrice

Dans l’exemple précédent, nous devions calculer la racine dixième d’un nombre. Ceci est différent de la prise de la racine carrée de base, √. De nombreuses calculatrices scientifiques ont un bouton pour les racines générales. Il est généralement étiqueté comme suit :

\sqrt{x}

Pour évaluer la 3ème racine de 8, par exemple, nous devrions soit taper 3 \sqrt{{}} 8, ou 8 \sqrt{}} 3, selon la calculatrice. Essayez sur la vôtre pour voir laquelle utiliser – vous devriez obtenir une réponse de 2.

Si votre calculatrice ne dispose pas d’un bouton de racine générale, tout n’est pas perdu. Vous pouvez plutôt utiliser la propriété des exposants qui stipule que :

\sqrt{a}={a}^{\frac{1}{2}}.

Donc, pour calculer la 3e racine de 8, vous pourriez utiliser la touche exposant de votre calculatrice pour évaluer 81/3. Pour ce faire, tapez :

8 yx ( 1 ÷ 3 )

Les parenthèses indiquent à la calculatrice de diviser 1/3 avant de faire l’exposant.

Essayez-le

Le nombre d’utilisateurs d’un site de réseautage social était de 45 mille en février lorsqu’ils sont devenus officiellement publics, et est passé à 60 mille en octobre. Si le site connaît une croissance exponentielle et que la croissance se poursuit au même rythme, combien d’utilisateurs doivent-ils s’attendre à avoir deux ans après leur entrée en bourse ?

Montrer la solution

Nous allons ici mesurer n en mois plutôt qu’en années, avec n = 0 correspondant au mois de février où ils sont entrés en bourse. Cela donne P_0= 45 mille. Octobre est 8 mois plus tard, donc P_8= 60.
P_8=(1+r)^{8}P_0
60=(1+r)^{8}45
\frac{60}{45}=(1+r)^8
\sqrt{\frac{60}{45}}=1+r
r=\sqrt{\frac{60}{45}}-1=0.0366\text{ ou }3,66%
L’équation explicite générale est P_n =(1,0366)^{n}45. En prédisant 24 mois après leur entrée en bourse, on obtient P_{24}=(1,0366)^{24}45=106,63 milliers d’utilisateurs.

Exemple

En reprenant le dernier exemple, à titre de comparaison, quelles seraient les émissions de carbone en 2050 si les émissions croissent linéairement au même rythme ?

Afficher la solution

De nouveau, nous obtiendrons que n = 0 corresponde à 1990, ce qui donne P0 = 962. Pour trouver d, nous pourrions adopter la même approche que précédemment, en notant que les émissions ont augmenté de 220 millions de tonnes métriques en 10 ans, ce qui donne une différence commune de 22 millions de tonnes métriques chaque année.

Alternativement, nous pourrions utiliser une approche similaire à celle que nous avons utilisée pour trouver l’équation exponentielle. Lorsque n = 10, l’équation linéaire explicite ressemble à :

P10 = P0 + 10d

Nous connaissons la valeur de P0, nous pouvons donc la mettre dans l’équation :

P10 = 962 + 10d

Puisque nous savons que P10 = 1182, en le substituant, nous obtenons

1182 = 962 + 10d

Nous pouvons maintenant résoudre cette équation pour la différence commune, d.

1182 – 962 = 10d

220 = 10d

d = 22

Cela nous indique que si les émissions évoluent linéairement, elles augmentent de 22 millions de tonnes métriques chaque année. En prédisant les émissions en 2050,

P60 = 962 + 22(60) = 2282 millions de tonnes métriques.

Vous remarquerez que ce nombre est sensiblement plus petit que la prédiction du modèle de croissance exponentielle. Le calcul et le tracé d’autres valeurs permettent d’illustrer les différences.

Une démonstration de cet exemple peut être vue dans la vidéo suivante.

Alors, comment savoir quel modèle de croissance utiliser lorsqu’on travaille avec des données ? Il y a deux approches qui devraient être utilisées ensemble autant que possible :

1. Trouvez plus de deux données. Tracez les valeurs, et recherchez une tendance. Les données semblent-elles évoluer comme une ligne, ou les valeurs semblent-elles se courber vers le haut ?
2. Considérez les facteurs qui contribuent aux données. S’agit-il de choses dont vous vous attendriez à ce qu’elles changent de façon linéaire ou exponentielle ? Par exemple, dans le cas des émissions de carbone, nous pourrions nous attendre à ce que, en l’absence d’autres facteurs, elles soient étroitement liées aux valeurs de la population, qui ont tendance à changer de façon exponentielle.