Lärandemål

  • Bestäm om data eller ett scenario beskriver linjär eller geometrisk tillväxt
  • Identifiera tillväxthastigheter, begynnelsevärden eller punktvärden som uttrycks muntligt och grafiskt, eller numeriskt, och översätta dem till ett format som kan användas i beräkningar
  • Beräkna rekursiva och explicita ekvationer för linjär och geometrisk tillväxt givet tillräcklig information, och använda dessa ekvationer för att göra förutsägelser

Att ha en konstant förändringshastighet är den definierande egenskapen för linjär tillväxt. Om man plottar koordinatpar som är förknippade med konstant förändring får man en rak linje, vilket är formen för linjär tillväxt. I det här avsnittet kommer vi att formalisera ett sätt att beskriva linjär tillväxt med hjälp av matematiska termer och begrepp. I slutet av detta avsnitt kommer du att kunna skriva både rekursiva och explicita ekvationer för linjär tillväxt med givna startvillkor eller en förändringskonstant. Du kommer också att kunna känna igen skillnaden mellan linjär och geometrisk tillväxt givet en graf eller en ekvation.

Linjär (algebraisk) tillväxt

Förutsägelse av tillväxt

Marco är en samlare av antika läskflaskor. Hans samling innehåller för närvarande 437 flaskor. Varje år budgeterar han tillräckligt med pengar för att köpa 32 nya flaskor. Kan vi bestämma hur många flaskor han kommer att ha om 5 år och hur lång tid det tar för hans samling att nå 1000 flaskor?

Samtidigt som du förmodligen skulle kunna lösa båda dessa frågor utan ekvation eller formell matematik kommer vi att formalisera vårt tillvägagångssätt för att ge ett sätt att besvara mer komplicerade frågor.

Förutsätt att Pn representerar antalet, eller populationen, av flaskor som Marco har efter n år. Så P0 skulle representera antalet flaskor nu, P1 skulle representera antalet flaskor efter 1 år, P2 skulle representera antalet flaskor efter 2 år och så vidare. Vi skulle kunna beskriva hur Marcos flasksamling förändras med hjälp av:

P0 = 437

Pn = Pn-1 + 32

Detta kallas ett rekursivt förhållande. Ett rekursivt förhållande är en formel som relaterar nästa värde i en sekvens till de föregående värdena. Här kan man få fram antalet flaskor år n genom att lägga till 32 till antalet flaskor föregående år, Pn-1. Med hjälp av detta förhållande kan vi beräkna:

P1 = P0 + 32 = 437 + 32 = 469

P2 = P1 + 32 = 469 + 32 = 501

P3 = P2 + 32 = 501 + 32 = 533

P4 = P3. + 32 = 533 + 32 = 565

P5 = P4 + 32 = 565 + 32 = 597

Vi har besvarat frågan om hur många flaskor Marco kommer att ha om fem år.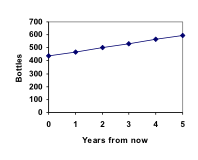

För att lösa hur lång tid det kommer att ta för hans samling att nå 1000 flaskor krävs dock många fler beräkningar.

Och även om rekursiva relationer är utmärkta för att på ett enkelt och rent sätt beskriva hur en kvantitet förändras, så är de inte lämpliga för att göra förutsägelser eller lösa problem som sträcker sig långt in i framtiden. För detta är en sluten eller explicit form för förhållandet att föredra. En explicit ekvation gör att vi kan beräkna Pn direkt, utan att behöva känna till Pn-1. Även om du kanske redan kan gissa den explicita ekvationen, låt oss härleda den från den rekursiva formeln. Det kan vi göra genom att selektivt låta bli att förenkla under tiden:

P1 = 437 + 32 = 437 + 1(32)

P2 = P1 + 32 = 437 + 32 + 32 = 437 + 2(32)

P3 = P2 + 32 = (437 + 2(32)) + 32 = 437 + 3(32)

P4 = P3 + 32 = (437 + 3(32)) + 32 = 437 + 4(32)

Du kan förmodligen se mönstret nu och generalisera att

Pn = 437 + n(32) = 437 + 32n

Med hjälp av denna ekvation kan vi beräkna hur många flaskor han kommer att ha efter 5 år:

P5 = 437 + 32(5) = 437 + 160 = 597

Vi kan nu också lösa när samlingen kommer att nå 1000 flaskor genom att ersätta 1000 för Pn och lösa n

1000 = 437 + 32n

563 = 32n

n = 563/32 = 17.59

Så Marco kommer att nå 1 000 flaskor på 18 år.

Stegen för att bestämma formeln och lösa problemet med Marcos flaskinsamling förklaras i detalj i följande videoklipp.

I det här exemplet ökade Marcos samling med samma antal flaskor varje år. Denna konstanta förändring är den definierande egenskapen för linjär tillväxt. Genom att plotta de värden som vi beräknade för Marcos samling kan vi se att värdena bildar en rak linje, vilket är formen för linjär tillväxt.

Linjär tillväxt

Om en kvantitet börjar vid storleken P0 och växer med d varje tidsperiod kan kvantiteten efter n tidsperioder bestämmas med hjälp av någon av dessa relationer:

Rekursiv form

Pn = Pn-1 + d

Explicit form

Pn = P0 + d n

I denna ekvation representerar d den gemensamma differensen – den mängd som populationen ändras varje gång n ökar med 1.

Koppling till tidigare lärande: Du kanske känner igen den gemensamma skillnaden, d, i vår linjära ekvation som lutning. Faktum är att hela den explicita ekvationen borde se bekant ut – det är samma linjära ekvation som du lärde dig i algebra, troligen formulerad som y = mx + b.

I den algebraiska standardekvationen y = mx + b var b y-interceptet, eller y-värdet när x var noll. I den ekvationsform som vi använder använder vi P0 för att representera den inledande mängden.

I ekvationen y = mx + b minns du att m var lutningen. Du kanske kommer ihåg detta som ”rise over run”, eller förändringen i y dividerat med förändringen i x. Oavsett vilket så representerar det samma sak som den gemensamma skillnaden, d, som vi använder – den mängd som utgången Pn förändras när ingången n ökar med 1.

Ekvationerna y = mx + b och Pn = P0 + d n betyder samma sak och kan användas på samma sätt. Vi skriver det bara något annorlunda.

Exempel

Populationen av älgar i en nationalskog uppmättes till 12 000 år 2003 och uppmättes igen till 15 000 år 2007. Om populationen fortsätter att växa linjärt i denna takt, hur stor kommer älgpopulationen att vara 2014?

Visa lösning

För att börja måste vi definiera hur vi ska mäta n. Kom ihåg att P0 är populationen när n = 0, så vi vill antagligen inte bokstavligen använda oss av år 0. Eftersom vi redan känner till befolkningen år 2003, låt oss definiera n = 0 som år 2003.

Då är P0 = 12 000.

Nästan måste vi hitta d. Kom ihåg att d är tillväxten per tidsperiod, i det här fallet tillväxten per år. Mellan de två mätningarna ökade befolkningen med 15 000-12 000 = 3 000, men det tog 2007-2003 = 4 år att växa så mycket. För att hitta tillväxten per år kan vi dividera: För att bestämma tillväxten på ett år kan vi dividera: 3000 älgar / 4 år = 750 älgar på 1 år.

Alternativt kan du använda formeln för lutning från algebra för att bestämma den gemensamma skillnaden, varvid du noterar att populationen är formelns utdata och tiden är inmatningen.

d=slope=\frac{\text{changeinoutput}}{\text{changeinput}}=\frac{15 000-12 000}{2007-2003}=\frac{3000}{4}=750

Vi kan nu skriva vår ekvation i vilken form som helst.

Rekursiv form

P0 = 12 000

Pn = Pn-1 + 750

Explicit form

Pn = 12 000 + 750(n)

För att besvara frågan måste vi först konstatera att året 2014 blir n = 11, eftersom 2014 är 11 år efter 2003. Den explicita formen är lättare att använda för denna beräkning:

P11 = 12 000 + 750(11) = 20 250 älgar

Visa mer om detta exempel här.

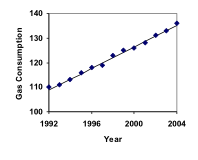
Bensinkonsumtionen i USA har ökat stadigt. Förbrukningsdata från 1992 till 2004 visas nedan. Hitta en modell för dessa data och använd den för att förutsäga konsumtionen 2016. Om trenden fortsätter, när kommer förbrukningen att nå 200 miljarder gallon?

>

>

År ’92 ’93 ’94 ’95 ’96 ’97 ’98 ’99 ’00 ’01 ’02 ’03 ’04
Konsumtion (miljarder euro) gallon) 110 111 113 116 118 119 123 125 126 128 131 133 136
Visa lösning

Plottning av dessa data, verkar de ha ett ungefärligt linjärt samband:

Men det finns mer avancerade statistiska tekniker som kan användas för att hitta en ekvation för att modellera data, och för att få en uppfattning om vad som händer kan vi hitta en ekvation genom att använda två delar av data – kanske data från 1993 och 2003.

Om n = 0 motsvarar 1993 skulle det ge P0 = 111 miljarder gallon.

För att hitta d måste vi veta hur mycket gasförbrukningen ökade varje år i genomsnitt. Från 1993 till 2003 ökade gasförbrukningen från 111 miljarder gallon till 133 miljarder gallon, en total förändring på 133 – 111 = 22 miljarder gallon, under 10 år. Detta ger oss en genomsnittlig förändring på 22 miljarder gallon / 10 år = 2,2 miljarder gallon per år.

Ekvivalent

d=slope=\frac{\text{changeinoutput}}{\text{changeinput}}=\frac{133-111}{10-0}=\frac{22}{10}=2.2 miljarder gallon per år

Vi kan nu skriva vår ekvation i vilken form som helst.

Rekursiv form

P0 = 111

Pn = Pn-1 + 2.2

Explicit form

Pn = 111 + 2.2n

Att beräkna värden med hjälp av den explicita formen och plotta dem tillsammans med originaldata visar hur väl vår modell stämmer överens med data.

Vi kan nu använda vår modell för att göra förutsägelser om framtiden, under förutsättning att den tidigare trenden fortsätter oförändrad. För att förutsäga bensinkonsumtionen 2016:

n = 23 (2016 – 1993 = 23 år senare)

P23 = 111 + 2,2(23) = 161,6

Vår modell förutsäger att USA kommer att konsumera 161.6 miljarder gallon bensin år 2016 om den nuvarande trenden fortsätter.

För att ta reda på när förbrukningen kommer att nå 200 miljarder gallon skulle vi ställa in Pn = 200 och lösa för n:

Pn = 200 Ersätt Pn med vår modell

111 + 2.2n = 200 Subtrahera 111 från båda sidorna

2.2n = 89 Dela båda sidorna med 2.2

n = 40.4545

Detta säger oss att konsumtionen kommer att nå 200 miljarder ungefär 40 år efter 1993, vilket skulle vara år 2033.

Stråken för att nå detta svar beskrivs i detalj i följande video.

Kostnaden, i dollar, för ett medlemskap i ett gym i n månader kan beskrivas med den explicita ekvationen Pn = 70 + 30n. Vad säger oss denna ekvation?

Visa lösningen

Värdet för P0 i denna ekvation är 70, så den ursprungliga startkostnaden är 70 dollar. Detta säger oss att det måste finnas en initierings- eller startavgift på 70 dollar för att gå med i gymmet.

Värdet för d i ekvationen är 30, så kostnaden ökar med 30 dollar varje månad. Detta säger oss att den månatliga medlemsavgiften för gymmet är 30 dollar i månaden.

Förklaringen till detta exempel beskrivs närmare nedan.

Try It

Antalet familjefäder i Kanada har ökat stadigt. Även om trenden inte är helt linjär är den ganska linjär. Använd uppgifterna från 1976 och 2010 för att hitta en uttrycklig formel för antalet pappor som stannar hemma och använd den sedan för att förutsäga antalet år 2020.

År 1976 1984 1991 2000 2010
Antal stannande hemma-home fathers 20610 28725 43530 47665 53555
Visa lösning

Låt n= 0 motsvara 1976, så är P_0= 20 610.
Från 1976 till 2010 ökade antalet hemmavarande pappor med 53 555 – 20 610 = 32 945
Detta skedde under 34 år, vilket ger ett gemensamt annorlunda d på 32 945 / 34 = 969.
P_n= 20 610 + 969n
För att förutsäga för 2020 använder vi n = 44, P(44) = 20 610 + 969(44) = 63 246 familjefäder år 2020.

När bra modeller blir dåliga

När man använder matematiska modeller för att förutsäga ett framtida beteende är det viktigt att komma ihåg att mycket få trender kommer att fortsätta i all oändlighet.

Exempel

Antag att en fyraårig pojke för närvarande är 39 tum lång, och att du har blivit informerad om att du förväntar dig att han kommer att växa 2,5 tum per år.

Vi kan ställa upp en tillväxtmodell, där n = 0 motsvarar 4 års ålder.

Rekursiv form

P0 = 39

Pn = Pn-1 + 2,5

Explicit form

Pn = 39 + 2.5(n)

Så vid 6 års ålder skulle vi förvänta oss att han är

P2 = 39 + 2.5(2) = 44 tum lång

Alla matematiska modeller kommer att brytas ner till slut. Vi bör definitivt inte förvänta oss att den här pojken ska fortsätta att växa i samma takt hela livet. Om han gjorde det skulle han vid 50 års ålder vara

P46 = 39 + 2,5(46) = 154 tum lång = 12,8 fot lång!

När vi använder en matematisk modell måste vi överväga vilka indata som är rimliga att använda. När vi extrapolerar eller gör förutsägelser i framtiden antar vi att modellen kommer att fortsätta att vara giltig.

Se en videoförklaring av denna uppdelning av den linjära tillväxtmodellen här.

Exponentiell (Geometrisk ) tillväxt

Populationstillväxt

Förutsatt att varje år har endast 10 % av fiskarna i en sjö överlevande avkommor. Om det fanns 100 fiskar i sjön förra året skulle det nu finnas 110 fiskar. Om det fanns 1 000 fiskar i sjön förra året skulle det nu finnas 1 100 fiskar. I avsaknad av hämmande faktorer tenderar populationer av människor och djur att växa med en procent av den befintliga populationen varje år.


Antag att vår sjö började med 1 000 fiskar och att 10 % av fiskarna har överlevande avkommor varje år. Eftersom vi börjar med 1000 fiskar är P0 = 1000. Hur beräknar vi P1? Den nya populationen kommer att vara den gamla populationen plus ytterligare 10 %. Symboliskt:

P1 = P0 + 0,10P0

Märk att detta skulle kunna kondenseras till en kortare form genom att faktorisera:

P1 = P0 + 0,10P0 = 1P0 + 0,10P0 = (1+ 0,10)P0 = 1,10P0

Och medan 10 % är tillväxthastigheten är 1,10 tillväxtmultiplikatorn. Observera att 1,10 kan ses som ”de ursprungliga 100 % plus ytterligare 10 %”

För vår fiskpopulation

P1 = 1,10(1000) = 1100

Vi kan sedan beräkna populationen under senare år:

P2 = 1,10P1 = 1,10(1100) = 1210

P3 = 1,10P2 = 1,10(1210) = 1331

Observera att under det första året ökade populationen med 100 fiskar, under det andra året ökade populationen med 110 fiskar och under det tredje året ökade populationen med 121 fiskar.

Medans det är en konstant procentuell tillväxt, ökar den faktiska ökningen av antalet fiskar varje år.

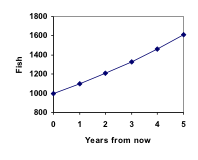
Graferar vi dessa värden ser vi att denna tillväxt inte riktigt verkar linjär.

En genomgång av detta fiskscenario kan ses här:

För att få en bättre bild av hur den här procentuella tillväxten påverkar saker och ting behöver vi en explicit form, så att vi snabbt kan beräkna värden längre fram i tiden.

Som vi gjorde för den linjära modellen kommer vi att börja bygga från den rekursiva ekvationen:

P1 = 1,10(P0 )= 1,10(1000)

P2 = 1,10(P1 )= 1,10(1,10(1000)) = 1,102(1000)

P3 = 1.10(P2 )= 1.10(1.102(1000)) = 1.103(1000)

P4 = 1.10(P3 )= 1.10(1.103(1000)) = 1.104(1000)

Observerar vi ett mönster kan vi generalisera den explicita formen till att vara:

Pn = 1.10n(1000), eller motsvarande, Pn = 1000(1.10n)

Därmed kan vi snabbt beräkna antalet fiskar om 10, 20 eller 30 år:

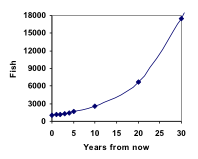
P10 = 1.1010(1000) = 2594

P20 = 1.1020(1000) = 6727

P30 = 1.1030(1000) = 17449

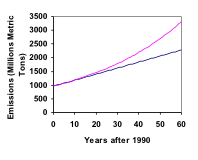
Om vi lägger till dessa värden i vår graf får vi fram en form som definitivt inte är linjär. Om vår fiskpopulation hade vuxit linjärt, med 100 fiskar varje år, skulle populationen bara ha nått 4 000 på 30 år, jämfört med nästan 18 000 med denna procentbaserade tillväxt, som kallas exponentiell tillväxt.

En video som visar den explicita modellen för den här fiskhistorien kan ses här:

I exponentiell tillväxt växer populationen proportionerligt till storleken på populationen, så när populationen blir större kommer samma procentuella tillväxt att ge en större numerisk tillväxt.

Exponentiell tillväxt

Om en kvantitet börjar vid storlek P0 och växer med R% (skrivet som en decimal, r) varje tidsperiod, kan kvantiteten efter n tidsperioder bestämmas med hjälp av någon av dessa relationer:

Rekursiv form

Pn = (1+r) Pn-1

Explicit form

Pn = (1+r)n P0 eller motsvarande, Pn = P0 (1+r)n

Vi kallar r för tillväxttakten.

Uttrycket (1+r) kallas tillväxtmultiplikator, eller gemensam kvot.

Exempel

Mellan 2007 och 2008 växte Olympia, WA med nästan 3 % till en befolkning på 245 tusen personer. Om denna tillväxttakt skulle fortsätta, hur stor skulle Olympias befolkning vara 2014?

Visa lösning

Som vi gjorde tidigare måste vi först definiera vilket år som ska motsvara n = 0. Eftersom vi känner till befolkningen 2008 är det rimligt att låta 2008 motsvara n = 0, så P0 = 245 000. Året 2014 skulle då vara n = 6.

Vi vet att tillväxttakten är 3 %, vilket ger r = 0,03.

Med hjälp av den explicita formen:

P6 = (1+0,03)6 (245 000) = 1,19405(245 000) = 292 542,25

Modellen förutspår att Olympia år 2014 skulle ha en befolkning på cirka 293 tusen personer.

I följande video förklaras det här exemplet i detalj.

Utvärdering av exponenter på miniräknaren

För att utvärdera uttryck som (1,03)6 blir det lättare att använda en miniräknare än att multiplicera 1,03 med sig själv sex gånger. De flesta vetenskapliga miniräknare har en knapp för exponenter. Den är vanligtvis antingen märkt som:

^ , yx , eller xy .

För att utvärdera 1,036 skulle vi skriva 1,03 ^ 6, eller 1,03 yx 6. Prova dig fram – du bör få ett svar runt 1,1940523.

Prova dig fram

Indien är det näst folkrikaste landet i världen, med en befolkning 2008 på cirka 1,14 miljarder människor. Befolkningen växer med cirka 1,34 procent varje år. Om denna trend fortsätter, vad kommer Indiens befolkning att växa till år 2020?

Visa lösning

Med n = 0 som motsvarar 2008 blir P_12= (1+0,0134)12(1,14) = ungefär 1.337 miljarder människor år 2020

Exempel

En vän använder ekvationen Pn = 4600(1,072)n för att förutsäga den årliga terminsavgiften vid ett lokalt college. Hon säger att formeln är baserad på år efter 2010. Vad säger ekvationen?

Visa lösning

I ekvationen är P0 = 4600, vilket är startvärdet för terminsavgiften när n = 0. Detta säger oss att terminsavgiften år 2010 var 4 600 dollar.

Växlingsmultiplikatorn är 1,072, så tillväxttakten är 0,072, eller 7,2 %. Detta säger oss att terminsavgiften förväntas öka med 7,2 % varje år.

Sammantaget kan vi säga att terminsavgiften 2010 var 4 600 dollar och förväntas öka med 7,2 % varje år.

Visa följande för att se hur exemplet är utformat.

Under 1990 stod bostädernas energianvändning i USA för 962 miljoner ton koldioxidutsläpp. År 2000 hade den siffran stigit till 1182 miljoner ton. Om utsläppen ökar exponentiellt och fortsätter i samma takt, vad kommer utsläppen att öka till år 2050?

Visa lösningen

Som tidigare kommer vi att korrespondera n = 0 med 1990, eftersom det är året för den första data vi har. Det ger P0 = 962 (miljoner ton koldioxid). I det här problemet får vi inte tillväxttakten, utan får i stället veta att P10 = 1182.

När n = 10 ser den explicita ekvationen ut på följande sätt:

P10 = (1+r)10 P0

Vi känner till värdet för P0, så vi kan sätta in det i ekvationen:

P10 = (1+r)10 962

Vi vet också att P10 = 1182, så genom att sätta in det får vi

1182 = (1+r)10 962

Vi kan nu lösa ekvationen för tillväxttakten r. Börja med att dividera med 962.

\frac{1182}{962}={{(1+r)}^{10}}} Ta den tionde roten av båda sidor

\sqrt{\frac{1182}{962}}}=1+r Subtrahera 1 från båda sidor

r=\sqrt{\frac{1182}{962}}}-1=0,0208 = 2,08%

Om utsläppen växer exponentiellt så ökar de alltså med ungefär 2,08% per år. Vi kan nu förutsäga utsläppen år 2050 genom att hitta P60

P60 = (1+0,0208)60 962 = 3308,4 miljoner ton koldioxid år 2050

Visa mer om detta exempel här.

Avrundning

Som en anmärkning om avrundning kan du notera att om vi hade avrundat tillväxttakten till 2,1 % skulle vår beräkning av utsläppen 2050 ha varit 3347. En avrundning till 2 % skulle ha ändrat vårt resultat till 3156. En mycket liten skillnad i tillväxttakten blir kraftigt förstorad vid exponentiell tillväxt. Därför rekommenderas det att avrunda tillväxttakten så lite som möjligt.

Om du behöver avrunda, behåll minst tre signifikanta siffror – siffror efter eventuella inledande nollor. Så 0,4162 kan rimligen avrundas till 0,416. En tillväxttakt på 0,001027 kan rimligen avrundas till 0,00103.

Utvärdering av rötter på miniräknaren

I det föregående exemplet var vi tvungna att beräkna den tionde roten av ett tal. Detta är annorlunda än att ta den grundläggande kvadratroten √. Många vetenskapliga miniräknare har en knapp för allmänna rötter. Den är vanligtvis märkt på följande sätt:

\sqrt{x}

För att utvärdera den 3:e roten av 8, till exempel, skulle vi antingen skriva 3 \sqrt{{{}} 8, eller 8 \sqrt{{{}} 8 \sqrt{{{{}} 3, beroende på miniräknaren. Prova på din för att se vilken du ska använda – du bör få svaret 2.

Om din miniräknare inte har en allmän rotknapp är inte allt förlorat. Du kan istället använda exponenternas egenskap som säger att:

\sqrt{a}={a}^{\frac{1}{2}}}.

För att beräkna 3:e roten av 8 kan du alltså använda din miniräknares exponentknapp för att utvärdera 81/3. För att göra detta skriver du:

8 yx ( 1 ÷ 3 )

Parenteserna talar om för miniräknaren att den ska dividera 1/3 innan den gör exponenten.

Att prova

Antalet användare på en webbplats för sociala nätverk var 45 tusen i februari när de officiellt gick ut på marknaden, och ökade till 60 tusen i oktober. Om webbplatsen växer exponentiellt och tillväxten fortsätter i samma takt, hur många användare kan de förvänta sig två år efter det att de blev offentliga?

Visa lösningen

Här kommer vi att mäta n i månader i stället för i år, där n = 0 motsvarar februari när de blev offentliga. Detta ger P_0= 45 tusen. Oktober är 8 månader senare, så P_8= 60.
P_8=(1+r)^{8}P_0
60=(1+r)^{8}45
\frac{60}{45}=(1+r)^8
\sqrt{\frac{60}{45}}=1+r
r=\sqrt{\frac{60}{45}}-1=0.0366\text{ eller }3.66%
Den allmänna explicita ekvationen är P_n =(1.0366)^{n}45. Att förutsäga 24 månader efter att de blev offentliga ger P_{24}=(1,0366)^{24}45=106,63 tusen användare.

Exempel

Om vi tittar tillbaka på det senaste exemplet, för jämförelsens skull, vad skulle koldioxidutsläppen vara 2050 om utsläppen ökar linjärt i samma takt?

Visa lösningen

Även här får vi n = 0 som motsvarar 1990, vilket ger P0 = 962. För att hitta d kan vi använda samma tillvägagångssätt som tidigare och konstatera att utsläppen ökade med 220 miljoner ton på tio år, vilket ger en gemensam skillnad på 22 miljoner ton varje år.

Alternativt kan vi använda ett tillvägagångssätt som liknar det vi använde för att hitta exponentialekvationen. När n = 10 ser den explicita linjära ekvationen ut på följande sätt:

P10 = P0 + 10d

Vi känner till värdet för P0, så vi kan sätta in det i ekvationen:

P10 = 962 + 10d

Då vi vet att P10 = 1182, får vi genom att sätta in det

1182 = 962 + 10d

Vi kan nu lösa denna ekvation för den gemensamma differensen, d.

1182 – 962 = 10d

220 = 10d

d = 22

Detta säger oss att om utsläppen förändras linjärt ökar de med 22 miljoner ton varje år. Om vi förutspår utsläppen år 2050,

P60 = 962 + 22(60) = 2282 miljoner ton.

Du kommer att märka att denna siffra är betydligt mindre än förutsägelsen från den exponentiella tillväxtmodellen. Att beräkna och plotta fler värden hjälper till att illustrera skillnaderna.

En demonstration av det här exemplet kan ses i följande video.

Hur vet vi då vilken tillväxtmodell vi ska använda när vi arbetar med data? Det finns två tillvägagångssätt som bör användas tillsammans när det är möjligt:

  1. Hitta mer än två uppgifter. Plotta värdena och leta efter en trend. Ser uppgifterna ut att förändras som en linje, eller ser värdena ut att kurva uppåt?
  2. Konsultera de faktorer som bidrar till uppgifterna. Är det saker som du skulle förvänta dig förändras linjärt eller exponentiellt? När det gäller koldioxidutsläpp skulle vi till exempel kunna förvänta oss att de, utan andra faktorer, skulle vara nära knutna till befolkningsvärdena, som tenderar att förändras exponentiellt.

By: adminPosted on

Lämna ett svar

Din e-postadress kommer inte publiceras.