Introducere
În informatică, un graf aciclic dirijat (DAG) este un graf dirijat fără cicluri. În acest tutorial, vom arăta cum să facem o sortare topologică pe un DAG în timp liniar.
Sortare topologică
În multe aplicații, folosim grafuri aciclice dirijate pentru a indica precedențele între evenimente. De exemplu, într-o problemă de programare, există un set de sarcini și un set de constrângeri care specifică ordinea acestor sarcini. Putem construi un DAG pentru a reprezenta sarcinile. Marginile direcționate ale DAG-ului reprezintă ordinea sarcinilor.
Să luăm în considerare o problemă legată de modul în care o persoană se poate îmbrăca pentru o ocazie formală. Trebuie să ne punem mai multe articole de îmbrăcăminte, cum ar fi șosete, pantaloni, pantofi etc. Unele articole de îmbrăcăminte trebuie să fie puse înaintea celorlalte. De exemplu, trebuie să ne punem șosetele înainte de pantofi. Unele articole de îmbrăcăminte pot fi puse în orice ordine, de exemplu, șosetele și pantalonii. Putem folosi un DAG pentru a ilustra această problemă:
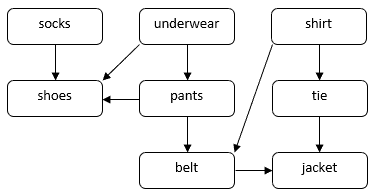
În acest DAG, vârfurile corespund hainelor. O muchie directă 
în DAG indică faptul că trebuie să ne punem haina 
înainte de haina 
. Sarcina noastră este de a găsi o ordine în care să îmbrăcăm toate hainele, respectând în același timp constrângerile de dependență. De exemplu, putem îmbrăca hainele în următoarea ordine:
O sortare topologică a unui DAG 
este o ordonare liniară a tuturor vârfurilor sale astfel încât, dacă conține o muchie , atunci apare înaintea lui în ordine. Pentru un DAG, putem construi o sortare topologică cu un timp de execuție liniar față de numărul de vârfuri plus numărul de muchii, care este 
.
Algoritmul lui Kahn
Într-un DAG, orice cale între două vârfuri are o lungime finită, deoarece graful nu conține un ciclu. Fie 
cea mai lungă cale de la (vîrful sursă) la (vîrful destinație). Deoarece este cea mai lungă cale, nu poate exista nicio muchie de intrare către . Prin urmare, un DAG conține cel puțin un vârf care nu are o muchie de intrare.
3.1. Algoritmul lui Kahn
În algoritmul lui Kahn, construim o sortare topologică pe un DAG prin găsirea vârfurilor care nu au muchii de intrare:
În acest algoritm, mai întâi calculăm valorile in-degree pentru toate vârfurile.
Apoi, începem cu un vârf al cărui in-degree este 0 și îl punem la sfârșitul listei de ieșire. Odată ce alegem un vertex, actualizăm valorile in-degree ale vârfurilor sale adiacente, deoarece vertexul și marginile sale de ieșire sunt eliminate din graf.
Potem repeta procesul de mai sus până când alegem toate vârfurile. Lista de ieșire este atunci o sortare topologică a grafului.
3.2. Complexitatea în timp
Pentru a calcula gradele înăuntru ale tuturor vârfurilor, trebuie să vizităm toate vârfurile și marginile din . Prin urmare, timpul de execuție este de pentru calculele in-degree. Pentru a evita calcularea din nou a acestor valori, putem utiliza o matrice pentru a ține evidența valorilor in-degree ale acestor vârfuri. În interiorul buclei while, trebuie, de asemenea, să vizităm toate vârfurile și marginile. Prin urmare, timpul total de execuție este de .
Depth First Search
Potem utiliza, de asemenea, un algoritm de căutare în profunzime (DFS) pentru a construi sortarea topologică. Graf DFS cu recursivitate
Înainte de a aborda aspectul sortării topologice cu DFS, să începem prin a trece în revistă un algoritm standard, recursiv de traversare DFS a grafurilor:
În algoritmul DFS standard, începem cu un vertex aleatoriu în și marcăm acest vertex ca fiind vizitat. Apoi, apelăm recursiv funcția dfsRecursive pentru a vizita toate verticele sale adiacente nevizitate. În acest fel, putem vizita toate vârfurile din în timp.
Dar, deoarece punem fiecare vârf în listă imediat ce îl vizităm și deoarece putem începe de la orice vârf, algoritmul DFS standard nu poate garanta generarea unei liste ordonate topologic.
Să vedem ce trebuie să facem pentru a rezolva acest neajuns.
4.2. Algoritmul de sortare topologică bazat pe DFS
Potem modifica algoritmul DFS pentru a genera o sortare topologică a unui DAG. În timpul parcurgerii DFS, după ce toți vecinii unui vertex sunt vizitați, îl punem în fruntea listei de rezultate 
. În acest fel, ne putem asigura că apare înaintea tuturor vecinilor săi în lista sortată:
Acest algoritm este similar cu algoritmul DFS standard. Deși începem tot cu un vertex aleatoriu, nu introducem vertexul în listă imediat ce îl vizităm. În schimb, vizităm mai întâi toți vecinii săi în mod recursiv și apoi punem vertexul în fruntea listei. Prin urmare, dacă conține o muchie , atunci apare înaintea lui în listă.
Timpul total de execuție este, de asemenea, , deoarece are aceeași complexitate în timp ca și algoritmul DFS.
Concluzie
În acest articol, am arătat un exemplu de sortare topologică pe un DAG. De asemenea, am discutat doi algoritmi care pot realiza o sortare topologică în timp.
Implementarea Java a algoritmului de sortare topologică bazat pe DFS este disponibilă în articolul nostru despre Depth First Search in Java.
.