Probabilitate > Probabilitate posterioară & distribuția posterioară
Ce este probabilitatea posterioară?
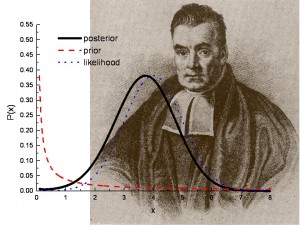
Probabilitățile posterioare sunt utilizate în testarea Bayesiană a ipotezelor. Imagine: Los Alamos National Lab.
Probabilitatea posterioară este probabilitatea ca un eveniment să se întâmple după ce toate dovezile sau informațiile de fond au fost luate în considerare. Este strâns legată de probabilitatea anterioară, care este probabilitatea ca un eveniment să se întâmple înainte de a lua în considerare orice nouă dovadă. Vă puteți gândi la probabilitatea posterioară ca la o ajustare a probabilității anterioare:
De exemplu, datele istorice sugerează că aproximativ 60% dintre studenții care încep o facultate vor absolvi în termen de 6 ani. Aceasta este probabilitatea anterioară. Cu toate acestea, credeți că această cifră este de fapt mult mai mică, așa că vă propuneți să colectați noi date. Dovezile pe care le colectați sugerează că adevărata cifră este de fapt mai aproape de 50%; Aceasta este probabilitatea posterioară.
Originea termenilor
Cuvântul posterior și anterior provin din latinescul a priori. Definiția cuvântului „a priori” este:
„…referitor la ceea ce poate fi cunoscut prin înțelegerea modului în care funcționează anumite lucruri mai degrabă decât prin observație” ~ Miriam Webster.
Opusul lui „a priori” este a posteriori, care este definit ca fiind:
„… referitor la ceea ce poate fi cunoscut mai degrabă prin observație decât prin înțelegerea modului în care funcționează anumite lucruri” ~ Miriam Webster.
Ce este o distribuție posterioară?
Distribuția posterioară este o modalitate de a rezuma ceea ce știm despre cantitățile incerte în analiza bayesiană. Este o combinație a distribuției anterioare și a funcției de verosimilitate, care vă spune ce informații sunt conținute în datele observate (noile „dovezi”). Cu alte cuvinte, distribuția posterioară sintetizează ceea ce știți după ce datele au fost observate. Rezumatul dovezilor din noile observații este funcția de verosimilitate.
Distribuțiile posterioare sunt de o importanță vitală în analiza bayesiană. Ele reprezintă în multe privințe scopul analizei și vă pot oferi:
- Stimări intermediare pentru parametri,
- Stimări punctuale pentru parametri,
- Inferență de predicție pentru datele viitoare,
- Evaluări probabilistice pentru ipoteza dumneavoastră.
Stephanie Glen. „Posterior Probability & the Posterior Distribution” From StatisticsHowTo.com: Statistică elementară pentru noi toți ceilalți! https://www.statisticshowto.com/posterior-distribution-probability/
——————————————————————————
Nevoie de ajutor cu o temă pentru acasă sau o întrebare de test? Cu Chegg Study, puteți obține soluții pas cu pas la întrebările dvs. de la un expert în domeniu. Primele 30 de minute cu un tutore Chegg sunt gratuite!