Operații pe rând în matrice

Întoarceți la Indexul lecțiilor | Parcurgeți lecțiile în ordine | Pagină ușor de tipărit

Operații pe rând în matrice (pagina 1 din 2)

„Operații” este un termen matematic pentru „proceduri”. Cele patru „operații de bază” asupra numerelor sunt adunarea, scăderea, înmulțirea și împărțirea. Pentru matrici, există trei operații de bază pe rânduri; adică, există trei proceduri pe care le puteți face cu rândurile unei matrice.

Prima operație este comutarea rândurilor. De exemplu, dată fiind matricea:

…puteți schimba rândurile pentru a pune matricea într-un aranjament mai frumos al rândurilor, astfel:

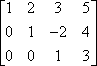
Comutarea rândurilor este adesea indicată prin desenarea de săgeți, astfel:

Când schimbați rândurile, aveți grijă să copiați corect intrările.

A doua operație este înmulțirea rândurilor. De exemplu, dată fiind următoarea matrice:

…puteți înmulți primul rând cu -1 pentru a obține o valoare inițială pozitivă în primul rând:

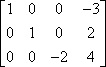
Această înmulțire a rândurilor este adesea indicată prin utilizarea unei săgeți cu multiplicarea listată deasupra ei, astfel:

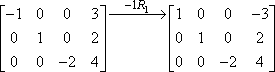
„-1R1” indică operația efectivă. „-1” spune că am înmulțit cu unu negativ; „R1” spune că am lucrat cu primul rând. Observați că al doilea și al treilea rând au fost copiate, neschimbate, în a doua matrice. Înmulțirea s-a aplicat doar primului rând, așa că intrările pentru celelalte două rânduri au fost pur și simplu transportate neschimbate.

Puteți înmulți cu orice doriți. De exemplu, pentru a obține un 1 principal în al treilea rând al matricei anterioare, puteți înmulți al treilea rând cu o jumătate negativă:

Din moment ce nu făceați nimic cu primul și al doilea rând, aceste intrări au fost pur și simplu copiate fără modificări în noua matrice.

Puteți face mai multe înmulțiri de rânduri în cadrul aceluiași pas, astfel încât ați fi putut face cei doi pași de mai sus într-un singur pas, astfel:

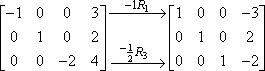
Este o idee bună să folosiți o anumită formă de notație (cum ar fi săgețile și indicele de mai sus), astfel încât să puteți ține evidența muncii dumneavoastră. Matricile sunt foarte dezordonate, mai ales dacă le faceți de mână, iar notele pot facilita verificarea ulterioară a muncii dumneavoastră. De asemenea, îl vor impresiona pe profesorul dumneavoastră.

Ultima operație pe rând este adunarea rândurilor. Adăugarea rândurilor este similară cu metoda „adunării” pentru rezolvarea sistemelor de ecuații liniare. Să presupunem că aveți următorul sistem de ecuații:

x + 3y = 1
-x + y = 3 Copyright © Elizabeth Stapel 2003-2011 Toate drepturile rezervate

Ați putea începe rezolvarea acestui sistem prin adunarea coloanelor în jos pentru a obține 4y = 4:

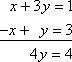
Puteți face ceva similar cu matrici.De exemplu, dată fiind următoarea matrice:

…puteți „reduce” (obține mai multe zerouri de început) al doilea rând prin adăugarea primului rând la acesta (obiectivul general cu matricile în această etapă fiind acela de a obține un „1” – sau „0-uri” și apoi un „1” – la începutul fiecărui rând al matricei). Atunci când ați redus sistemul liniar cu două ecuații prin adunare, ați trasat o bară de „egalitate” în partea de jos și ați adunat în jos. Atunci când folosiți adunarea pe o matrice, va trebui să luați niște hârtie de scris, deoarece nu doriți să încercați să faceți munca în interiorul matricei. Așadar, adunați cele două rânduri pe hârtia de desenat:

Lucrare de desenat – nu predați acest lucru!

Acesta este noul vostru al doilea rând; îl veți scrie în locul vechiului al doilea rând. Rezultatul va arăta astfel:

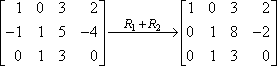
În acest caz, „R1 + R2” de pe săgeată înseamnă „Am adăugat rândul unu la rândul doi și acesta este rezultatul pe care l-am obținut”. Din moment ce rândul unu nu s-a schimbat de fapt și din moment ce nu am făcut nimic cu rândul trei, aceste rânduri sunt copiate în noua matrice neschimbate.

Top | 1 | 2 | Return to Index Next >>

Cită acest articol ca:

Stapel, Elizabeth. „Matrix Row Operations”. Purplemath. Disponibil la https://www.purplemath.com/modules/mtrxrows.htm. Accesat 2016

.