Precondiții – Bazele teoriei grafurilor – Set 1
Un graf este o structură care reprezintă un set de obiecte în care unele perechi de obiecte sunt într-un anumit sens „legate”. Obiectele din graf corespund vârfurilor, iar relațiile dintre ele corespund marginilor. Un graf este reprezentat schematic ca un set de puncte care reprezintă vârfuri conectate prin linii sau curbe care reprezintă muchii.
În mod formal,
„Un graf 
constă din 
, un set nevid de vârfuri (sau noduri) și 
, un set de muchii. Fiecărei muchii îi sunt asociate fie unul, fie două vârfuri, numite puncte terminale.”
Tipuri de grafuri :Există mai multe tipuri de grafuri care se disting pe baza muchiilor, a direcției lor, a greutății lor etc.
1. Graf simplu – Un graf în care fiecare muchie conectează două vârfuri diferite și în care nu există două muchii care să conecteze aceeași pereche de vârfuri se numește graf simplu. De exemplu, considerăm următorul graf –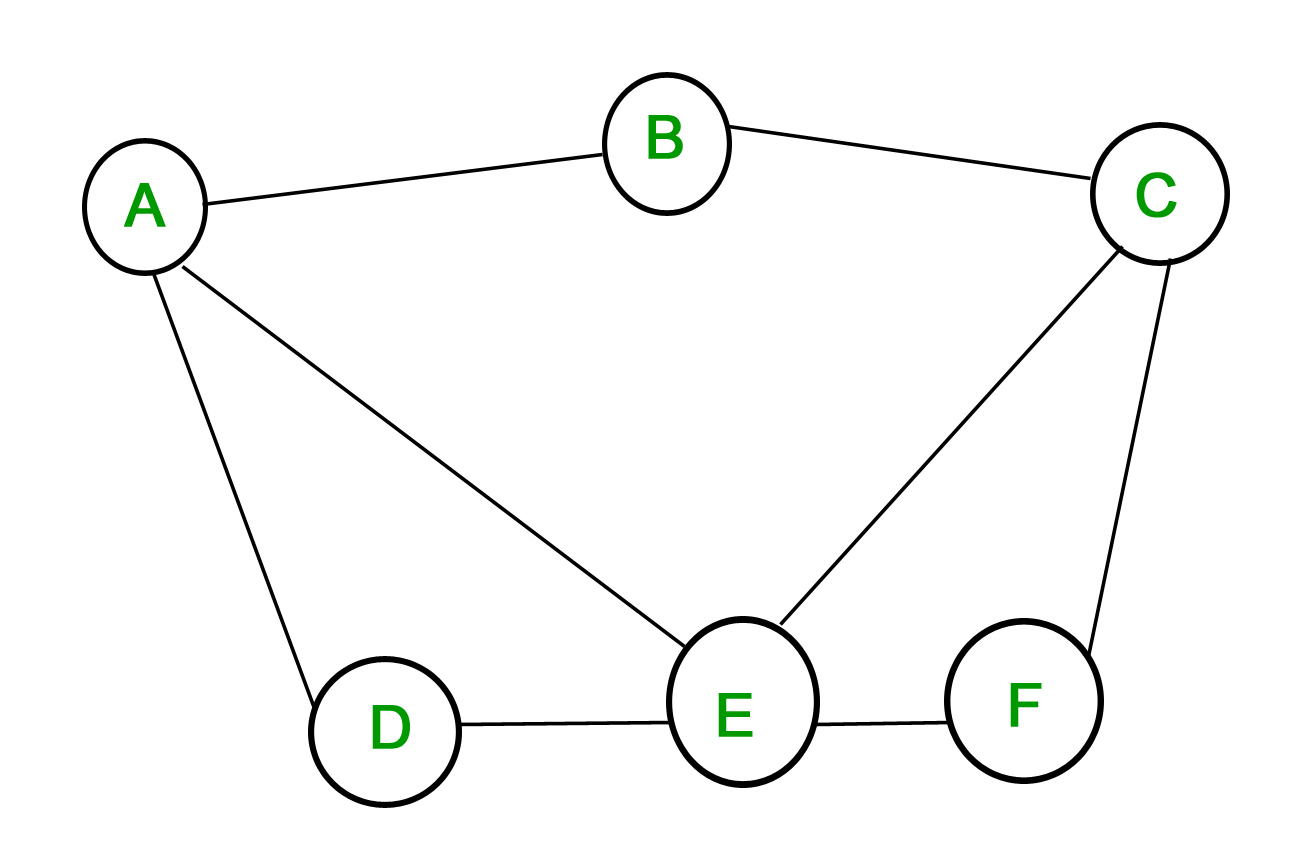
Graful de mai sus este un graf simplu, deoarece nici un vârf nu are o buclă proprie și nici două vârfuri nu au mai mult de o muchie care să le conecteze.
Arginile sunt notate prin vârfurile pe care le conectează- 
este muchia care conectează vârfurile 
și 
.
2. Multigraf – Un graf în care mai multe muchii pot conecta aceeași pereche de vârfuri se numește multigraf.
Din moment ce pot exista mai multe muchii între aceeași pereche de vârfuri, multiplicitatea muchiei indică numărul de muchii între două vârfuri.
Graful de mai sus este un multigraf deoarece există mai multe muchii între și 
. Multiplicitatea muchiei 
este 2.
În unele grafuri, spre deosebire de cel prezentat mai sus, muchiile sunt direcționate. Aceasta înseamnă că relația dintre obiecte este doar unidirecțională și nu bidirecțională. Direcția marginilor poate fi importantă în unele aplicații.
În funcție de faptul dacă marginile sunt direcționate sau nu, putem avea grafuri direcționate și grafuri nedirecționate. Această proprietate poate fi extinsă la grafuri simple și multigrafe pentru a obține grafuri simple dirijate sau nedirijate și multigrafe dirijate sau nedirijate.
Terminologie de bază a grafurilor :
În discuția de mai sus au fost deja explicați unii termeni referitoare la grafuri, cum ar fi vârfuri, muchii, muchii dirijate și nedirijate etc. Există mai mulți termeni care descriu proprietăți ale vârfurilor și marginilor.
- Adiacență – Într-un graf
se spune că două vârfuri 
și 
sunt adiacente dacă sunt punctele finale ale unei muchii. Se spune că muchia 
este incidentă cu vârfurile.
În cazul în care muchia este dirijată, se spune că este adiacentă lui , iar se spune că este adiacentă lui . Aici, se spune că este vârful inițial, iar se spune că este vârful terminal. - Gradul – Gradul unui vârf este numărul de muchii incidente cu acesta, cu excepția buclei proprii care contribuie de două ori la gradul vârfului. Gradul unui vertex se notează ca
.
În cazul grafurilor dirijate, gradul este clasificat în continuare în grad de intrare (in-degree) și grad de ieșire (out-degree). Gradul de intrare (in-degree) al unui vertex este numărul de muchii cu vertexul dat ca vertex terminal. Gradul de ieșire al unui vertex este numărul de muchii cu vertexul dat ca vertex inițial. Gradul de intrare este notat cu
, iar gradul de ieșire este notat cu 
.
De exemplu, în graficul direcționat prezentat mai sus, care descrie zborurile între orașe, gradul de intrare al vertexului „Delhi” este 3, iar gradul de ieșire al acestuia este, de asemenea, 3.
Nota: Dacă un vertex are gradul zero, acesta se numește izolat. Dacă gradul este unu, atunci se numește pandant.
Teorema de la Handshaking :
Ce se obține dacă se adună gradele tuturor vârfurilor unui graf. În cazul unui graf neorientat, fiecare muchie contribuie de două ori, o dată pentru vertexul său inițial și a doua oară pentru vertexul său terminal. Așadar, suma gradelor este egală cu dublul numărului de muchii. Acest fapt este enunțat în teorema handshaking.
Let be an undirected graph with edges. ThenIn case G is a directed graph,
Teorema handshaking, pentru grafuri nedirecționate, are un rezultat interesant –
An undirected graph has an even number of vertices of odd degree.
Probă : Fie 
și 
ansamblurile de vârfuri de grade pare și respectiv impare.
Știm prin teorema strângerii de mână că,
Atunci,
Suma gradelor vârfurilor cu grade pare este pară. LHS este de asemenea par, ceea ce înseamnă că suma gradelor vârfurilor cu grade impare trebuie să fie pară.
Atunci, numărul de vârfuri cu grad impar este par.
Câteva grafuri simple speciale :
1. Grafuri complete – Un graf simplu de 
vârfuri care are exact o muchie între fiecare pereche de vârfuri se numește graf complet. Un graf complet de vârfuri se notează cu 
. Numărul total de muchii este n*(n-1)/2 cu n vârfuri în graful complet.
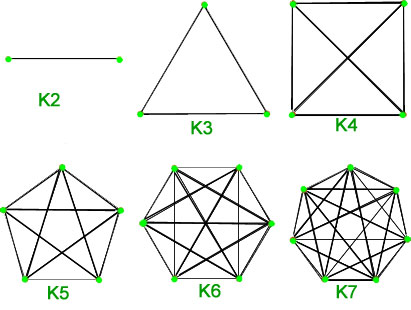
2. Ciclurile – Ciclurile sunt grafuri simple cu vârfuri 
și muchii 
. Ciclul cu vârfuri este notat cu 
. Numărul total de muchii este n cu n vârfuri în graful ciclului.
3. Roți – O roată este la fel ca un ciclu, cu un vârf suplimentar care este conectat la fiecare alt vârf. Roțile de vârfuri cu 1 verigă suplimentară sunt notate cu 
. Numărul total de muchii este 2*(n-1) cu n vârfuri în graful roți. 
4. Hipercubul – Hipercubul sau n-cubul este un graf cu 
vârfuri, fiecare fiind reprezentat de un șir de n biți. Verticile care diferă cu cel mult 1 bit sunt conectate prin muchii. Un hipercub de vârfuri este notat cu 
. Numărul total de muchii este n*
cu vârfuri în graful cub.
5. Grafuri bipartite – Un graf simplu se spune că este bipartit dacă setul său de vertexuri poate fi împărțit în două seturi disjuncte astfel încât fiecare muchie din să aibă vertexul inițial în primul set și vertexul terminal în cel de-al doilea set. Numărul total de muchii este (n*m) cu (n+m) vârfuri în graful bipartit.
Teorema – Un graf simplu este bipartit dacă și numai dacă este posibilă atribuirea uneia dintre cele două
culori diferite fiecărui vârf al grafului astfel încât să nu existe două vârfuri adiacente cărora să li se atribuie
aceeași culoare.
Un graf bipartit cu 
și vârfuri în cele două subseturi disjuncte ale sale se spune că este complet dacă există o muchie de la fiecare vârf din primul set la fiecare vârf din al doilea set, pentru un total de 
muchii. Un graf bipartit complet cu vârfuri în primul set și vârfuri în al doilea set se notează 
.
GATE CS Corner Questions
Practicarea următoarelor întrebări vă va ajuta să vă testați cunoștințele. Toate întrebările au fost puse în GATE în anii anteriori sau în testele simulate GATE. Este foarte recomandat să le exersați.
1. GATE CS 2013, Întrebare 25
2. GATE CS 2014 Set-1, Întrebare 61
3. GATE CS 2006, Întrebare 71
4. GATE CS 2002, Întrebare 25
5. GATE CS 2002, Întrebare 25
5. GATE CS 2004, Întrebare 37
6. GATE CS 2014 Set-2, Întrebare 13
Referințe-
Grafuri – Wikipedia
Discrete Mathematics and its Applications, de Kenneth H Rosen
Acest articol este realizat de Chirag Manwani. Dacă vă place GeeksforGeeks și doriți să contribuiți, puteți, de asemenea, să scrieți un articol folosind contribute.geeksforgeeks.org sau să trimiteți articolul prin poștă la [email protected]. Vedeți articolul dumneavoastră apărând pe pagina principală GeeksforGeeks și ajutați alți Geeks.
.