- Conectivitatea este un concept de bază al teoriei grafurilor. Acesta definește dacă un graf este conectat sau deconectat. Fără conectivitate, nu este posibilă parcurgerea unui graf de la un vertex la un alt vertex.
- Se spune că un graf este un graf conectat dacă există o cale între fiecare pereche de vertexuri. De la fiecare vertex la orice alt vertex trebuie să existe o cale de parcurs. Aceasta se numește conectivitatea unui graf.
- Un graf se spune că este deconectat, dacă există mai multe vârfuri și muchii deconectate.
- Teoriile conectivității grafurilor sunt esențiale în aplicațiile de rețea, rutarea rețelelor de transport, toleranța rețelelor etc.
Exemplu
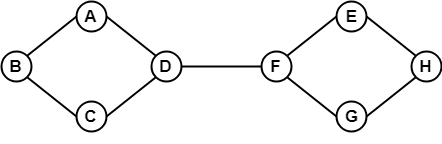
În exemplul de mai sus, este posibil să se călătorească de la un vertex la un alt vertex. Aici, putem traversa de la vertexul B la H folosind calea B -> A -> D -> F -> E -> H. Prin urmare, este un graf conex.
Exemplu
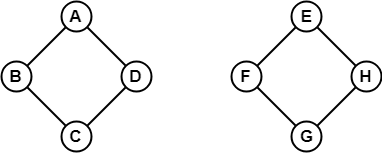
În exemplul de mai sus, nu este posibilă traversarea de la vertexul B la H, deoarece nu există nici o cale între ele direct sau indirect. Prin urmare, este un graf deconectat.
Să vedem câteva concepte de bază ale conectivității.
Cut Vertex
Un singur vârf a cărui eliminare deconectează un graf se numește cut-vertex.
Să fie G un graf conex. Un vertex v din G se numește un vertex tăiat al lui G, dacă G-v (Remove v from G) are ca rezultat un graf deconectat.
Când eliminăm un vertex dintr-un graf, atunci graful se va rupe în două sau mai multe grafuri. Acest vârf se numește vârf tăiat.
Nota: Fie G un graf cu n vârfuri:
- Un graf conex G poate avea maximum (n-2) vârfuri tăiate.
- Îndepărtarea unui vârf tăiat poate lăsa un graf deconectat.
- Îndepărtarea unui vârf poate crește numărul de componente ale unui graf cu cel puțin unul.
- Care vertex nependent al unui arbore este un vertex tăiat.
Exemplu 1

Exemplu 2
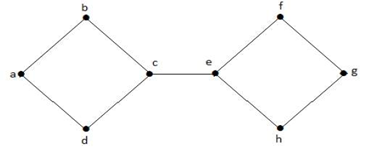
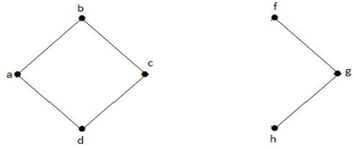
În graful de mai sus, vertexul ‘e’ este un vertex tăiat. După eliminarea vertexului ‘e’ din graful de mai sus, graful va deveni un graf deconectat.
Cut Edge (Bridge)
Un cut- Edge sau bridge este o singură muchie a cărei eliminare deconectează un graf.
Să fie G un graf conex. O muchie e din G se numește muchie tăiată a lui G, dacă G-e (Remove e from G) rezultă un graf deconectat.
Când eliminăm o muchie dintr-un graf, atunci graful se va rupe în două sau mai multe grafuri. Această muchie eliminată se numește muchie tăiată sau punte.
Nota: Fie G un graf cu n vârfuri:
- Un graf conex G poate avea cel mult (n-1) muchii tăiate.
- Îndepărtarea unei muchii tăiate poate lăsa un graf deconectat.
- Îndepărtarea unei muchii poate crește numărul de componente ale unui graf cu cel mult unu.
- O muchie tăiată „e” nu trebuie să facă parte din nici un ciclu în G.
- Dacă există o muchie tăiată, atunci trebuie să existe și un vertex tăiat, deoarece cel puțin un vertex al unei muchii tăiate este un vertex tăiat.
- Dacă există un vârf tăiat, atunci existența oricărei muchii tăiate nu este necesară.
Exemplu 1
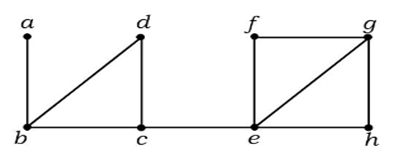
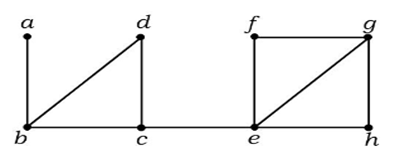
În graful de mai sus, muchia (c, e) este o muchie tăiată. După eliminarea acestei muchii din graficul de mai sus, graficul va deveni un grafic deconectat.
Exemplul 2
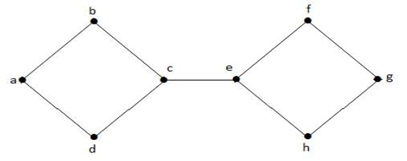
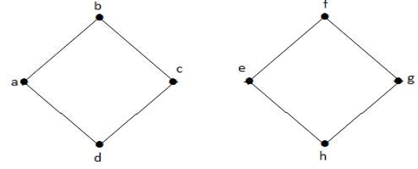
În graficul de mai sus, muchia (c, e) este o muchie tăioasă. După eliminarea acestei muchii din graful de mai sus, graful va deveni un graf deconectat.
Set de tăieri
Într-un graf conex G, un set de tăieri este un set S de muchii cu următoarele proprietăți:
- Îndepărtarea tuturor muchiilor din S deconectează G.
- Îndepărtarea unor muchii (dar nu a tuturor) din S nu deconectează G.
Exemplu 1
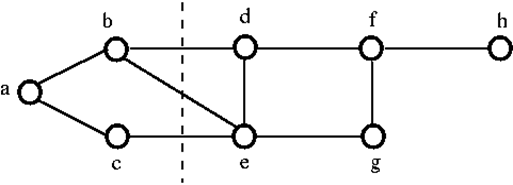
Pentru a deconecta graful G de mai sus, trebuie să îndepărtăm cele trei muchii. adică bd, be și ce. Nu îl putem deconecta prin eliminarea doar a două dintre cele trei muchii. Prin urmare, {bd, be, ce} este un set tăiat.
După eliminarea setului tăiat din graful de mai sus, acesta ar arăta după cum urmează:
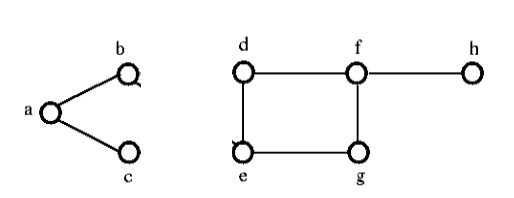
Conectivitatea marginilor
Conectivitatea marginilor unui graf conex G este numărul minim de muchii a căror eliminare face ca G să fie deconectat. Ea se notează cu λ(G).
Când λ(G) ≥ k, atunci se spune că graful G este k-conectat cu muchii.
Exemplu
Să vedem un exemplu,
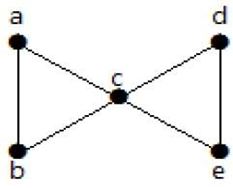
Din graful de mai sus, prin eliminarea a două muchii minime, graful conectat devine un graf deconectat. Prin urmare, conectivitatea marginilor sale este 2. Prin urmare, graful de mai sus este un graf conectat cu 2 muchii.
Iată următoarele patru moduri de deconectare a grafului prin eliminarea a două muchii:
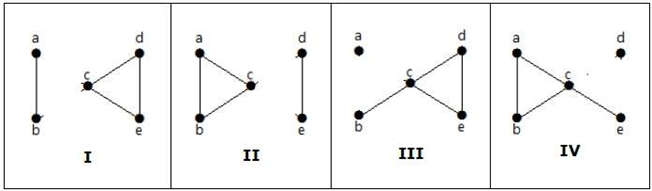
Conectivitatea vârfurilor
Conectivitatea (sau conectivitatea vârfurilor) unui graf conex G este numărul minim de vârfuri a căror eliminare face ca G să se deconecteze sau să se reducă la un graf trivial. Se notează cu K(G).
Se spune că un graf este k-conectat sau k-vertex conectat atunci când K(G) ≥ k. Pentru a elimina un vertex trebuie să eliminăm și marginile incidente acestuia.
Exemplu
Să vedem un exemplu:
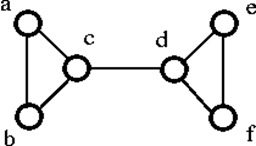
Graful G de mai sus poate fi deconectat prin îndepărtarea unui singur vertex, fie ‘c’, fie ‘d’. Prin urmare, conectivitatea vertexurilor sale este 1. Prin urmare, este un graf cu conectivitate 1.
.