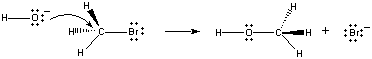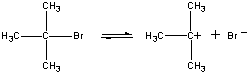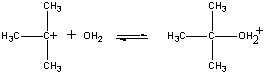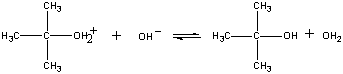Cinetică chimică
Cinetică chimică
Poate că sunteți familiarizați cu titrările acido-bazice care folosesc fenolftaleina ca indicator al punctului final. S-ar putea să nu fi observat, totuși, ce se întâmplă atunci când o soluție care conține fenolftaleină în prezența unui exces de bază este lăsată să stea în repaus timp de câtevaminute. Deși inițial soluția are o culoare roz, ea devine treptat incoloră deoarece fenolftaleina reacționează cu ionul OH- într-o soluție puternic bazică.
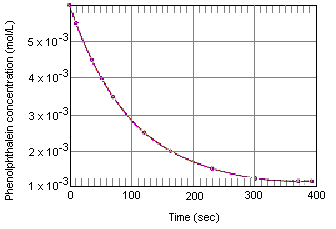
Tabelul de mai jos arată ce se întâmplă cu concentrația de fenolftaleină într-o soluție care a fost inițial 0,005 M în fenolftaleină și 0,61 M în ion OH-. După cum se poate observa atunci când aceste date sunt reprezentate în graficul de mai jos, concentrația de fenolftaleină scade de un factor de 10 pe o perioadă de aproximativ patru minute.
Date experimentale pentru reacția dintre fenolftaleină și excesul de bază
Experimente precum cel care ne-a furnizat datele din tabelul de mai sus suntclasificate ca măsurători de cinetică chimică (de la o tulpină grecească care înseamnă „a se mișca”). Unul dintre scopurile acestor experimente este de a descrie viteza de reacțieritmul în care reactanțiise transformă în produsele reacției.
Termenul viteză este adesea folosit pentru a descrie modificarea unei cantități care are loc pe unitate de timp. Rata inflației, de exemplu, este modificarea costului mediu al unei colecții de articole standard pe an. Viteza cu care un obiect se deplasează în spațiu este distanța parcursă pe unitate de timp, cum ar fi mile pe oră sau kilometri pe secundă. În cinetica chimică, distanța parcursă reprezintă modificarea concentrației unuia dintre componentele reacției. Viteza unei reacții este, prin urmare, modificarea concentrației unuia dintre reactanți
(X)
care are loc într-o anumită perioadă de timpt.
Problemă practică 1:
Utilizați datele din tabelul de mai sus pentru a calcula viteza cu care fenolftaleina reacționează cu ionul OH- în timpul fiecăreia dintre următoarele perioade:
(a) În timpul primului interval de timp, când concentrația de fenolftaleină scade de la 0,0050 M la 0,0045 M.
(b) În timpul celui de-al doilea interval, când concentrația scade de la 0,0045 M la 0,0040 M.
(c) În timpul celui de-al treilea interval, când concentrația scade de la 0,0040 M la 0,0035 M.
Click aici pentru a vă verifica răspunsul la Problema practică 1.
Click aici pentru a vedea soluția la Problema practică 1.
Ratele instantanee de reacție și legea vitezei pentru o reacție
Rata reacției dintre fenolftaleină și ionul OH nu este constantă; ea se modifică în timp. Ca majoritatea reacțiilor, viteza acestei reacții scade treptat pe măsură ce reactivii sunt consumați. Acest lucru înseamnă că viteza de reacție se schimbă în timp ce este măsurată.
Pentru a minimiza eroarea pe care acest lucru o introduce în măsurătorile noastre, pare recomandabil să se măsoare viteza de reacție pe perioade de timp care sunt scurte în comparație cu timpul necesar pentru ca reacția să aibă loc. Am putea încerca, de exemplu, să măsurăm modificarea infinitezimală mică a concentrațieid(X)care are loc într-o perioadă de timp infinitezimal de scurtăt. Raportul dintre acestecantități este cunoscut sub numele de viteza instantanee de reacție.
Viteza instantanee de reacție la orice moment în timp poate fi calculată dintr-un grafic al concentrației reactantului (sau produsului) în funcție de timp. Graficul de mai jos arată modul în care rata de reacție pentru descompunerea fenolftaleinei poate fi calculată dintr-un grafic al concentrației în funcție de timp. Viteza de reacție în orice moment în timp este egală cu panta tangentei trasate la această curbă în acel moment.
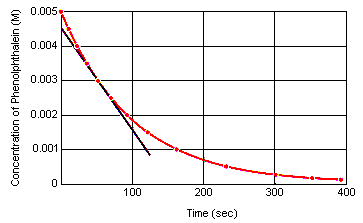
Rapiditatea instantanee a reacției poate fi măsurată în orice moment între momentul în care reactivii sunt amestecați și momentul în care reacția atinge echilibrul.Extrapolând aceste date până la momentul în care reactivii sunt amestecați, se obține viteza inițialăinstantanee a reacției.
Legi de viteză și constante de viteză
Un rezultat interesant se obține atunci când viteza instantanee a reacției este calculată în diferite puncte de-a lungul curbei din graficul din secțiunea precedentă. Viteza de reacție în fiecare punct de pe această curbă este direct proporțională cu concentrația de fenolftaleină în acel moment.
Viteza = k(fenolftaleină)
Pentru că această ecuație este o lege experimentală care descrie viteza de reacție, ea se numește legea vitezei pentru reacție. Constanta de proporționalitate, k, este cunoscută sub numele de constantă de viteză.
Problema practică 2:
Calculați constanta de viteză pentru reacția dintre fenolftaleină și ionul OH- dacă viteza instantanee de reacție este de 2,5 x 10-5 moli pe litru pe secundă atunci când concentrația de fenolftaleină este de 0,0025 M.
Click aici pentru a verifica răspunsul la Problema practică 2.
Click aici pentru a vedea o soluție la Problema practică 2.
Problema practică 3:
Utilizați constanta de viteză pentru reacția dintre fenolftaleină și ionul OH- pentru a calcula viteza inițială instantanee de reacție pentru datele experimentale enumerate în tabelul precedent.
Click aici pentru a vă verifica răspunsul la Problema practică 3.
Click aici pentru a vedea soluția la Problema practică 3.
Diferite moduri de exprimare a vitezei de reacție
De obicei există mai mult de un mod de a măsura viteza unei reacții. Putem studia descompunerea iodurii de hidrogen, de exemplu, prin măsurarea vitezei cu care se formează H2 sau I2 în următoarea reacție sau a vitezei cu care se consumă HI.
2 HI(g) H2(g) + I2(g)
Experimental constatăm că viteza cu care se formează I2 este proporțională cu pătratul concentrației de HI în orice moment de timp.
Ce s-ar întâmpla dacă am studia viteza cu care se formează H2?Ecuația echilibrată sugerează că H2 și I2 trebuie să se formeze exact cu aceeași viteză.
Ce s-ar întâmpla, totuși, dacă am studia viteza cu care se consumă HI în această reacție? Deoarece HI este consumat, modificarea concentrației sale trebuie să fie un număr negativ. Prin convenție, viteza unei reacții este întotdeauna raportată ca un număr pozitiv. Prin urmare, trebuie să schimbăm semnul înainte de a raporta viteza de reacție pentru unactant care este consumat în reacție.
Semnul negativ face două lucruri. Din punct de vedere matematic, el convertește o schimbare negativă a concentrației de HI într-o rată pozitivă. Din punct de vedere fizic, ne amintește căconcentrația reactivului scade cu timpul.
Care este relația dintre viteza de reacție obținută prin urmărirea formării de H2 sau I2 și viteza obținută prin urmărirea dispariției HI? Stoichiometria reacției spune că se consumă două molecule de HI pentru fiecare moleculă de H2 sau I2 produsă. Aceasta înseamnă că rata de descompunere a HI este de două ori mai rapidă decât rata de formare a H2 și I2. Putem transpune această relație într-o ecuație matematică după cum urmează.
Ca urmare, constanta de viteză obținută prin studierea vitezei cu care se formează H2și I2 în această reacție (k) nu este aceeași cu constanta de viteză obținută prin monitorizarea vitezei cu care se consumă HI (k’)
Problemă practică 4:
Calculați viteza cu care HI dispare în următoarea reacție în momentul în care I2 se formează cu o viteză de 1.8 x 10-6 moli pe litru pe secundă:
2 HI(g) 
H2(g) + I2(g)
Click aici pentru a verifica răspunsul la Problema practică 4.
Click aici pentru a vedea o soluție la Problema practică 4.
Legea vitezei față de stoichiometria unei reacții
În anii 1930, Sir Christopher Ingold și colaboratorii săi de la Universitatea dinLondra au studiat cinetica reacțiilor de substituție, cum ar fi următoarele.
CH3Br(aq) + OH-(aq)
CH3OH(aq) + Br-(aq)
Au constatat că viteza acestei reacții este proporțională cu concentrațiile ambilor reactanți.
Rata = k(CH3Br)(OH-)
Când au efectuat o reacție similară pe un material de pornire ușor diferit, au obținut produse similare.
(CH3)3CBr(aq) + OH-(aq)
Dar acum viteza de reacție era proporțională cu concentrația doar a unuia dintre reactanți.
Viteza = k((CH3)3CBr)
Aceste rezultate ilustrează un aspect important: Legea vitezei pentru oacțiune nu poate fi prezisă din stoichiometria reacției; ea trebuie să fie determinatăexperimental. Uneori, legea vitezei este în concordanță cu ceea ce ne așteptăm de la stoichiometria reacției.
2 HI(g) Rata = k(HI)2
Deseori, totuși, nu este așa.
2 N2O5(g) Rata = k(N2O5)
Ordine de molecularitate
Câteva reacții au loc într-o singură etapă. Reacția în care un atom de clor este transferat de la ClNO2 la NO pentru a forma NO2 și ClNO este un bunexemplu de reacție într-o singură etapă.
ClNO2(g) + NO(g)
Alte reacții au loc printr-o serie de etape individuale. N2O5,de exemplu, se descompune în NO2 și O2 printr-un mecanism în trei etape.
Etapa 1: N2O5 Etapa 2: NO2 + NO3 Etapa 3: : NO + NO3 Etapele unei reacții sunt clasificate în funcție de molecularitate,care descrie numărul de molecule consumate. Atunci când se consumă o singură moleculă, etapa se numește unimoleculară. Atunci când sunt consumate două molecule, este bimoleculară.
Problema practică 5:
Determinați molecularitatea fiecărei etape din reacția prin care N2O5 se descompune în NO2 și O2.
Click aici pentru a verifica răspunsul la Problema practică 5.
Click aici pentru a vedea o soluție la Problema practică 5.
Reacțiile pot fi clasificate și în funcție de ordinea lor. Descompunerea N2O5 este o reacție de ordinul întâi deoarece viteza de reacție depinde de concentrația de N2O5 ridicată la prima putere.
Viteză = k(N2O5)
Descompunerea HI este o reacție de ordinul doi deoarece viteza de reacție depinde de concentrația de HI ridicată la puterea a doua.
Rata = k(HI)2
Când viteza unei reacții depinde de mai mult de un reactiv, clasificăm reacția în funcție de ordinea fiecărui reactiv.
Problema practică 6:
Clasificați ordinea reacției dintre NO și O2 pentru a forma NO2:
2 NO(g) + O2(g)
Să presupunem următoarea lege de viteză pentru această reacție:
Rată = k(NO)2(O2)
Click aici pentru a verifica răspunsul la Problema practică 6.
Diferența dintre molecularitatea și ordinea unei reacții este importantă. Molecularitatea unei reacții, sau o etapă în cadrul unei reacții,descrie ceea ce se întâmplă la nivel molecular. Ordinea unei reacții descrie ceea ce se întâmplă la scară macroscopică. Determinăm ordinea unei reacții urmărind apariția produselor unei reacții sau dispariția reactanților. Molecularitatea reacției este ceva ce deducem pentru a explica aceste rezultate experimentale.
Modelul teoriei coliziunii al reacțiilor chimice
Modelul teoriei coliziunii al reacțiilor chimice poate fi folosit pentru a explica legile de viteză observate atât pentru reacții cu un singur pas, cât și pentru reacții cu mai mulți pași. Acest model presupune că viteza oricărei etape a unei reacții depinde de frecvența coliziunilor dintre particulele implicate în acea etapă.
Figura de mai jos oferă o bază pentru înțelegerea implicațiilor modelului teoriei coliziunii pentru reacții simple, cu o singură etapă, cum ar fi următoarele.
ClNO2(g) + NO(g)
Teoria cinetică moleculară presupune că numărul de coliziuni pe secundă într-un gaz depinde de numărul de particule pe litru. Viteza cu care se formează NO2și ClNO în această reacție ar trebui, prin urmare, să fie direct proporțională cu concentrațiile atât de ClNO2 cât și de NO.
Viteza = k(ClNO2)(NO)
Modelul teoriei coliziunii sugerează că viteza oricărei etape a unei reacții este proporțională cu concentrațiile reactivilor consumați în acea etapă. Legea vitezei pentru o reacție într-o singură etapă ar trebui, prin urmare, să fie în concordanță cu stoichiometria reacției.
Reacția următoare, de exemplu, are loc într-o singură etapă.
CH3Br(aq) + OH-(aq)
Când aceste molecule se ciocnesc în orientarea corespunzătoare, o pereche de electroni nelegat pe ionul OH- poate fi donată atomului de carbon din centrul moleculei CH3Br, așa cum se arată în figura de mai jos.
Când se întâmplă acest lucru, se formează o legătură carbon-oxigen în același timp cu ruperea legăturii carbon-bromin. Rezultatul net al acestei reacții este înlocuirea unui ion OH- cu un ion Br -. Deoarece reacția are loc într-o singură etapă, care implică coliziuni între cei doi reactanți, viteza acestei reacții este proporțională cu concentrația ambilor reactanți.
Rata = k(CH3Br)(OH-)
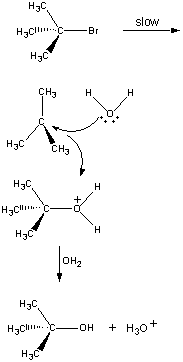
Nu toate reacțiile au loc într-o singură etapă. Următoarea reacție are loc în trei etape, așa cum se arată în figura de mai jos.
(CH3)3CBr(aq) + OH-(aq)
În prima etapă, molecula de (CH3)3CBr se disociază într-o pereche de ioni.
Prima etapă Ionul (CH3)3C+ încărcat pozitivreacționează apoi cu apa într-o a doua etapă.
Secunda etapă Produsul acestei reacții pierde apoi un proton fie către ionul OH, fie către apă în etapa finală.
Etapa a treia Etapele a doua și a treia din această reacție sunt foarte mult mai rapide decât prima.
(CH3)3CBr Etapă lentă (CH3)3C+ + H2O Etapă rapidă (CH3)3COH2+ + OH- Etapă rapidă Rapiditatea totală a reacției este, prin urmare, mai mult sau mai puțin egală cu viteza primei etape. Prima etapă se numește, prin urmare, etapa de limitare a vitezei în această reacție, deoarece limitează literalmente viteza cu care se pot forma produșii reacției. Deoarece numai un singur reactiv este implicat în etapa de limitare a vitezei, viteza totală a reacției este proporțională cu concentrația numai a acestui reactiv.
Viteză = k((CH3)3CBr)
Legea vitezei pentru această reacție diferă, prin urmare, de cea pe care am putea-o prezice din stoichiometria reacției. Deși reacția consumă atât (CH3)3CB cât și OH-, viteza reacției este doar proporțională cu concentrația de (CH3)3CBr.
Legile de viteză pentru reacțiile chimice pot fi explicate prin următoarele reguli generale.
Viteza oricărei etape a unei reacții este direct proporțională cu concentrațiile reactivilor consumați în acea etapă.
Legea vitezei globale a unei reacții este determinată de succesiunea etapelor sau de mecanismul prin care reactivii sunt transformați în produșii reacției.
Legea vitezei globale a unei reacții este dominată de legea vitezei pentru cea mai lentă etapă a reacției.
.