Difracția de raze X este o tehnică comună de caracterizare a materialelor care permite identificarea orientărilor cristaline și a spațiilor interatomice. Razele X sunt utilizate în acest scop deoarece lungimea de undă se află pe aceeași scară de lungime ca și distanța interatomică și valorile parametrilor de rețea.
Ce se întâmplă?
Un fascicul de raze X este generat într-un tub cu vid prin încălzirea unui filament de tungsten dincolo de funcția sa de lucru pentru a ejecta electroni. Condițiile de vid sunt necesare pentru a crește calea liberă medie a electronilor. Electronii sunt accelerați într-un catod de cupru cu o energie de ordinul a 25 keV. Coliziunile de electroni cu catodul de cupru duc la ionizări ale învelișului interior, producând raze X pe măsură ce electronii cu energie mai mare cad pentru a umple locul vacant cu energie mai mică. Electronii de la diferite niveluri energetice superioare cad, producând unde electromagnetice de energie variabilă. Astfel, sunt generate raze X cu lungimi de undă multiple (de tip K-beta și K-alfa). Pentru difracția razelor X, este ideal ca lumina monocromatică să interacționeze cu proba, astfel încât razele X de tip K-beta sunt filtrate cu o placă de nichel. Deși există într-adevăr două energii K-alfa asociate, energiile sunt atât de asemănătoare încât nu afectează în mod semnificativ profilul general al vârfurilor. Razele X trec printr-un colimator pentru a regla lățimea fasciculului.
Un mic istoric cu legea lui Bragg
Legea lui Bragg descrie relația pentru interferența constructivă, în care razele X de lungime de undă λ incidente pe material la un unghi θ sunt difractate de planurile cristaline separate de distanța d și n reprezintă un număr întreg.
Cum se vede mai jos, o schimbare de fază a undei provoacă fie interferență constructivă, așa cum se arată în stânga, fie interferență distructivă, reprezentată în dreapta, în funcție de unghiul 2θ.
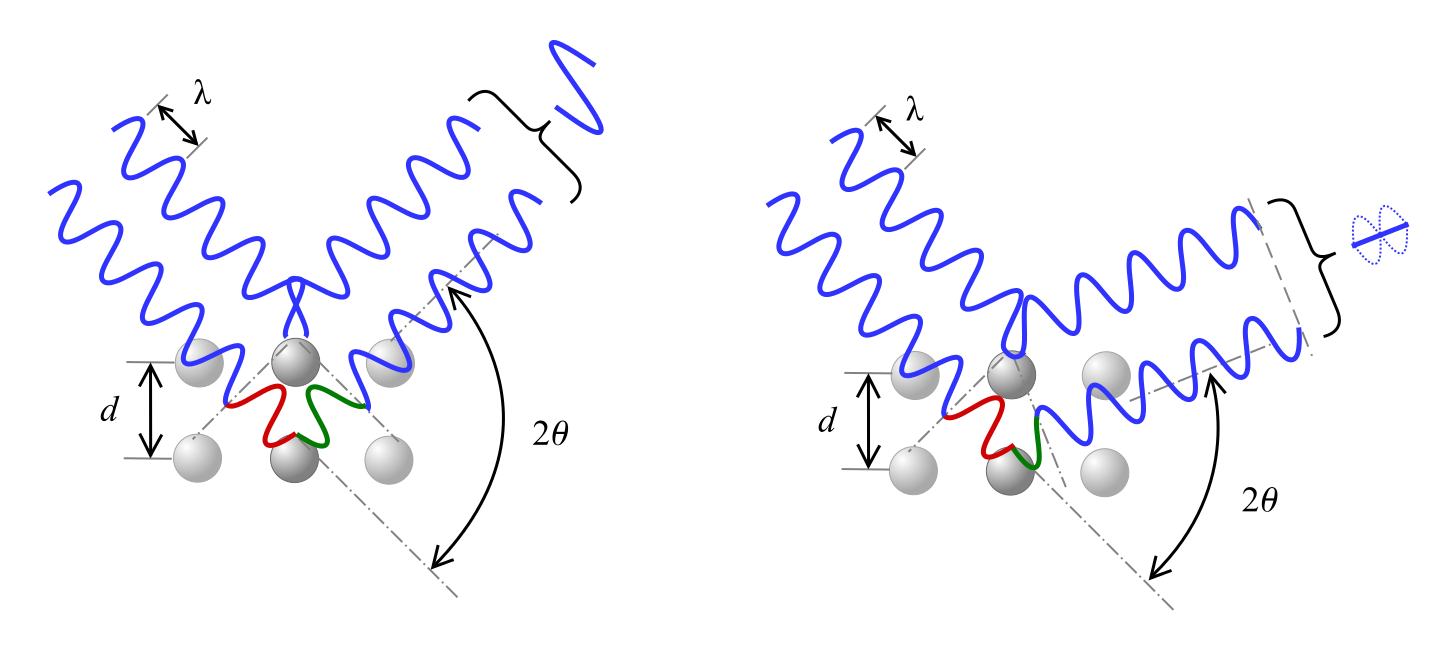
Ecuații pentru interpretarea rezultatelor XRD
Contorul, văzut mai jos într-o schemă a unui difractometru cu raze X, este rotit pe un interval de valori 2θ și înregistrează intensitatea semnalului de raze X reflectat de cristal în fiecare poziție. Această intensitate măsurată ca funcție de 2θ este utilizată pentru a genera un profil de vârf.
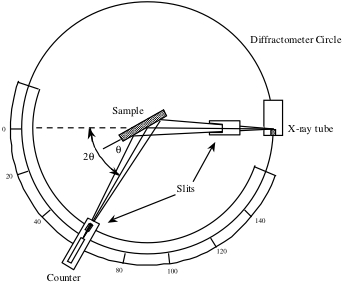
Pentru unghiurile care satisfac condiția Bragg, se va observa un vârf în semnalul de raze X datorită interferenței constructive. Aceste vârfuri sunt apoi folosite pentru a identifica direcțiile cristalului și pentru a calcula parametrii rețelei. Pentru sistemele cubice, distanța interplanară, d, poate fi calculată prin următoarea ecuație derivată din geometria cristalului, unde a este parametrul de rețea, iar h, k și l sunt indicii Miller.
Combinând legea lui Bragg și distanța interplanară se obține următoarea ecuație.
Aici, am mutat toate constantele în partea stângă a ecuației, permițându-ne să comparăm rapoartele valorilor sin2(θ) și indicii Miller între diferite vârfuri.
Când unda electromagnetică incidentă lovește materialul eșantionului, electronii care rezidă cu materialul sunt perturbați într-un model oscilant, care generează noi raze X și împrăștie efectiv undele luminoase incidente. Apar două tipuri de împrăștiere: împrăștierea coerentă sau elastică implică electroni oscilanți strâns legați care împrăștie raze X de aceeași lungime de undă și împrăștierea incoerentă care apare atunci când electronii slab legați sunt puși în mișcare oscilatorie și generează raze X de energie diferită. Difracția razelor X măsoară intensitatea razelor X împrăștiate coerent, care atinge vârfuri acolo unde unde undele interferează constructiv. Factorul de împrăștiere atomică poate fi definit ca un raport între amplitudinea undei împrăștiate de un atom și amplitudinea undei împrăștiate de un singur electron. Acest raport descrie, în esență, eficiența de împrăștiere a unui atom pentru o anumită direcție.
Exemplu de date XRD
Iată datele colectate în urma unui experiment pe care l-am făcut în timpul cursului de laborator de licență încercând să identific un metal necunoscut pe baza structurii sale cristaline.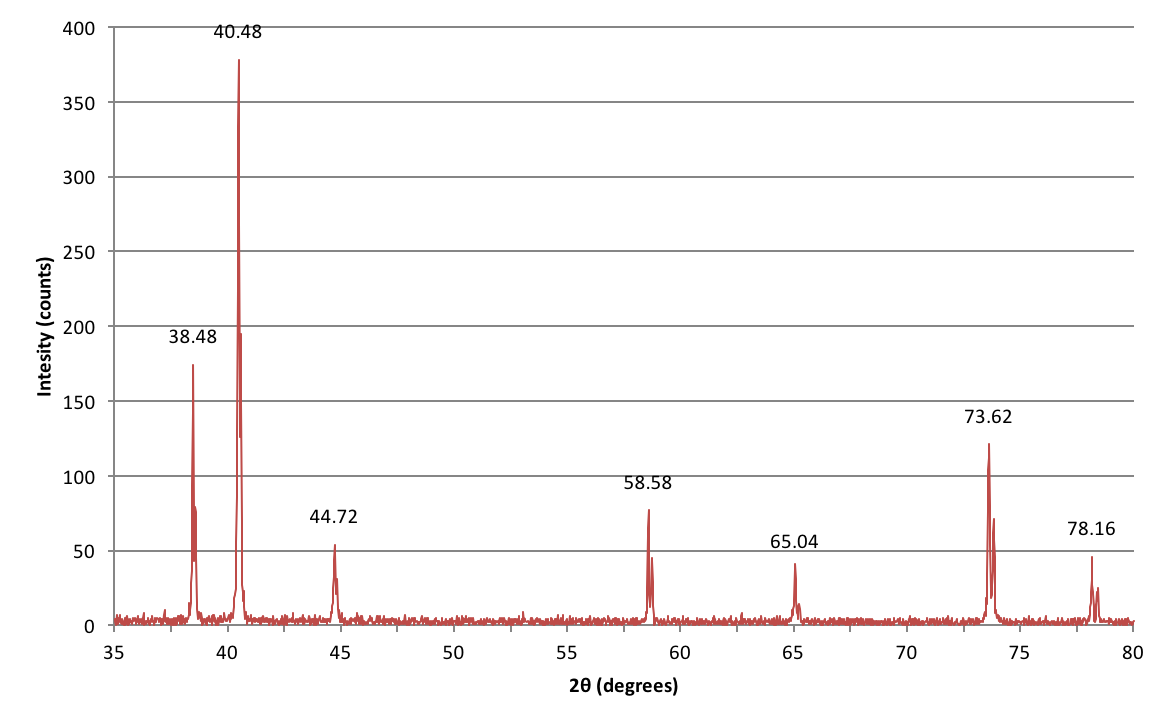
Cum interpretez aceste vârfuri?
| Structura cristalină | Condiții |
|---|---|
| Simplu cubic | toate h, k, l valorile |
| Cubic centrat pe corp | h+k+l trebuie să fie par |
| Cubic centrat pe față | h, k și l trebuie să fie toate impare sau toate pare |
Factorii de structură țin seama de cazurile în care un plan poate exista la jumătatea distanței dintre două planuri vecine și determină apariția interferențelor distructive. Acești factori au ca rezultat un set de reguli pentru diferite geometrii ale structurii cristaline care determină când poate apărea interferența constructivă. Tabelul de mai sus enumeră parametrii indicelui Miller în care se va produce interferența constructivă. Un tabel mai extins este prezentat mai jos. Prin compararea rapoartelor de sin2θ (notat ca $Q^2$ în cel de-al doilea tabel) pentru diferite vârfuri de difracție, se pot determina structura cristalină și indicii Miller.
| Planul cristalin (hkl) | $Q^2$ | Rețele spațiale din care sunt posibile reflexii | |||||
|---|---|---|---|---|---|---|---|
| 100 | 1 | SC | |||||
| 110 | 2 | SC | BCC | ||||
| 111 | 3 | SC | FCC | DC | |||
| 200 | 4 | SC | BCC | FCC | |||
| 210 | 5 | SC | SC | ||||
| 211 | 6 | SC | BCC | ||||
| – | 7 | ||||||
| 220 | 8 | SC | BCC | FCC | DC | ||
| 300, 221 | 9 | SC | |||||
| 310 | 10 | SC | BCC | ||||
| 311 | 11 | SC | FCC | DC | |||
| 222 | 12 | SC | BCC | FCC | FCC | ||
| 320 | 13 | SC | |||||
| 321 | 14 | SC | BCC | ||||
| – | 15 | ||||||
| 400 | 16 | SC | BCC | FCC | DC | ||
X-difracția de raze are o gamă largă de aplicații pentru caracterizarea materialelor. Ea poate fi utilizată ca metodă experimentală pentru a determina experimental volumul unei celule unitare pentru calculele teoretice de densitate. În plus, în cazul în care materialul este supus unei tensiuni reziduale, rețeaua distorsionată va prezenta o gamă de spații d care satisfac legea lui Bragg, rezultând astfel vârfuri de difracție mult mai largi. Lățimea vârfului de difracție poate fi, de asemenea, utilizată la determinarea dimensiunii particulelor.
.