Câte laturi are un cerc?

Este o întrebare de temă pentru școala primară care provoacă dezacord între matematicienii experimentați. Pentru a afla răspunsul corect, am apelat la cel mai riguros dintre instrumentele științifice, sondajul pe Twitter:

În retrospectivă, regret că nu am inclus o opțiune „niciuna dintre cele de mai sus”, dar mai multe despre asta mai târziu. În această postare voi trece în revistă aceste trei răspunsuri (și „niciunul dintre cele de mai sus”) și voi discuta avantajele și dezavantajele lor, așa cum le văd eu, înainte de a dezvălui în mod dramatic răspunsul corect.

Dar mai întâi: de ce nu putem da în mod direct răspunsul corect? Cuvintele din întrebare nu sunt deloc misterioase. Știm cu toții ce este un „cerc”, ce înseamnă să numeri „câte” din ceva și ce este o „latură”… sau nu? Iată definițiile (aproximative) pe care le-am distilat din discuțiile cu doi elevi de școală primară care au fost la capătul acestei întrebări:

1. O linie care face parte din limita unei forme a unei figuri plane.

Scopul de a spune figură plană mai degrabă decât „formă” aici este că dorim forme care trăiesc în 2 dimensiuni (de exemplu, pătrate sau cercuri, dar nu sfere sau cuburi). Următoarea întrebare este ce este o „linie” în definiția 1. Iată o variantă care o fixează:

2. Linie dreaptă care face parte din limita unei figuri plane.

Dacă tastați „definește: latură” în Google, cea mai relevantă definiție este:

O figură rectilinie este o figură construită din linii drepte. Așadar, această definiție este un rafinament al definiției 2 și ne permite să afirmăm că un pătrat are patru laturi, dar, la prima vedere, nu are nimic de spus despre figurile plane nerectilinii, cum ar fi cercurile.

Infinit de multe laturi?

Cred că este un pariu sigur că cei care au răspuns la sondajul meu pe Twitter au un nivel de educație matematică mai ridicat decât media națională. Faptul că au fost împărțiți cu privire la această întrebare și că o mică majoritate a selectat un răspuns care este destul de bine indisponibil pentru publicul obișnuit al acestei întrebări (elevi de școală primară), sugerează cu siguranță că ceva nu merge bine undeva.

Atunci, are un cerc infinit de multe laturi? Este cu siguranță util să considerăm un cerc ca fiind limita poligoanelor cu n laturi, pe măsură ce n devine din ce în ce mai mare. Aceasta este exact abordarea pe care Arhimede, Liu Hui și nenumărați alții au folosit-o de-a lungul secolelor pentru a studia geometria circulară, inclusiv pentru a ajunge la aproximări pentru π.

O ediție din secolul al XVI-lea din dinastia Ming a Jiuzhang suanshu (Nouă capitole despre arta matematică), secolul al III-lea d.Hr.

Câteodată este absolut sensibil, ca o prescurtare convenabilă, să ne gândim la un cerc ca fiind ca un poligon cu infinit de multe laturi.

Dar, ca un pedant insuportabil un matematician, aș vrea să fac distincția între prescurtarea convenabilă și adevărul literal. Dacă suntem ferm convinși că un cerc este într-adevăr un poligon cu infinit de multe laturi, atunci se pune întrebarea: care sunt laturile? Și, cu siguranță, singurul răspuns plauzibil este: punctele individuale ale cercului. Cât de lungi sunt aceste așa-zise laturi? Zero centimetri. Și sunt aceste laturi separate de colțuri? Aparent nu, fie că nu există deloc colțuri, fie că fiecare punct este atât o latură cât și un colț.

Am spune că laturile de lungime zero sunt… un concept problematic. Cum vă puteți da seama dacă aveți vreunul? De exemplu, să presupunem că studiez un sistem în care un pătrat apare ca limită a octogonelor, astfel:

În această situație, ar putea avea sens pentru mine să mă gândesc la pătratul meu ca având opt laturi, dintre care patru au lungimea zero. Dar dacă aș insista că pătratul meu (perfect obișnuit) are într-adevăr opt laturi, ați putea ridica o sprânceană.

Așa că acesta – răspunsul câștigător în sondajul meu – este singurul pe care îl voi declara ca fiind definitiv greșit, în timp ce este, de asemenea, singurul care oferă vreo perspectivă geometrică. Un paradox? Nu chiar. Raționamentul prin analogie este o abilitate valoroasă în matematică și în viață; în același timp, este important să ne menținem conștientizarea faptului că asta este ceea ce facem.

Pentru infinit de multe laturi: iluminator din punct de vedere geometric.
Contra infinit de multe laturi: pătrate cu opt laturi.

Pe tangentă 1: apeirogoni

Chiar dacă un cerc nu este unul, există poligoane cu infinit de multe laturi? Ei bine, există un cuvânt pentru a descrie un astfel de lucru un apeirogon. Un apeirogon regulat ar avea atunci laturi de lungime egală (diferită de zero) cu unghiuri egale între ele. Singura opțiune aici este acest obiect stupefiant de neexcitabil:

Dacă obiectați că acesta este un „poligon” (fie din cauza unghiurilor de 180°, fie din cauza lanțului de muchii care nu se închide în buclă), ce ziceți de ceva de genul acesta: începeți de la baza unui cerc, iar la fiecare etapă vă deplasați în jurul a jumătate din ceea ce a rămas din cerc și înlocuiți arcul pe care tocmai l-ați parcurs cu o muchie dreaptă:

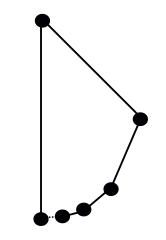
Este acesta un poligon autentic? Încă o dată, depinde de termenii pe care îi folosiți. Conform unei definiții comune, cea a unui „lanț poligonal închis”, acesta nu se califică, deoarece colțul de pornire (stânga jos) se conectează doar la o singură muchie. Dar este foarte aproape de ratare: acel punct este limita unei secvențe de muchii dinspre dreapta, ceea ce face ca această formă să fie o „curbă închisă neintersectată liniar pe bucățele”, o altă definiție a poligonului pe care oamenii o folosesc.

Dacă părăsim lumea noastră euclidiană obișnuită și intrăm în spațiul hiperbolic, atunci nu mai există nicio ambiguitate. Apeirogonii (chiar și apeirogonii regulați) există pur și simplu:

Un tiling al planului hiperbolic cu apeirogoni regulați. (De Anton Sherwood – Operă proprie, Domeniu public, https://commons.wikimedia.org/w/index.php?curid=13260274 )

Pe o tangentă 2: puncte extreme

S-ar putea fi mai ușor de susținut să spunem că un cerc are infinit de multe colțuri decât infinit de multe laturi (deși aceasta nu este o întrebare care pare să fie pusă foarte des). Pentru început, dacă un colț al unui pătrat este un punct în care linia de delimitare a acestuia nu este dreaptă, atunci fiecare punct de pe cerc satisface acest lucru. În mod mai sofisticat, există o noțiune de punct extrem al unei forme: acesta este orice punct prin care se poate trasa un segment de dreaptă care atinge forma doar în acel punct exact. Pentru un pătrat și pentru multe forme cunoscute, punctele extreme coincid exact cu colțurile. Fiecare punct de pe limita cercului este un punct extrem, astfel încât este cu siguranță adevărat că un cerc are un număr infinit de puncte extreme.

Am putea să ne îngrijorăm că unele forme, cum ar fi acest chevron, au colțuri care nu sunt puncte extreme:

Aici colțul central inferior nu este un punct extrem (celelalte trei colțuri sunt). Ceea ce nu merge bine este că această formă nu este convexă (în linii mari, are niște bucăți care ies prea mult în afară). Un cerc este convex, așa că poate nu trebuie să ne facem griji. Alternativ, am putea remedia situația prin definirea unui „colț” ca fiind un punct care este un punct extrem fie al formei în cauză, fie al complementului său, adică întregul plan cu forma decupată din el. Această abordare ar detecta colțurile tuturor poligoanelor, inclusiv ale chevronului. În cazul curbelor netede, ar identifica toate punctele de limită ca fiind „colțuri”, cu excepția punctelor de inflexiune (ceea ce nu este nerezonabil, deoarece am putea argumenta că acolo limita este dreaptă).

O singură latură?

În școala primară, se pare că „unu” este răspunsul care primește bifă. Și există o justificare moderat de decentă. Amintiți-vă definiția 1 de mai sus:

1. O linie care face parte din limita unei figuri plane.

Întrebarea imediată este ce contează ca „linie”, mai ales dacă nu insistăm pe rectiliniu. Dacă suntem prea relaxați în această privință, atunci se poate spune că orice figură plană are „o latură”, în același sens în care are o limită, un perimetru sau o circumferință. Dar acest lucru trebuie să fie greșit, deoarece cu siguranță dorim ca un pătrat să aibă patru laturi. Ei bine, un pătrat are patru puncte în care nu este neted, cu patru secțiuni netede între ele. Poate că noi am numărat tot timpul secțiunile netede. Așa că, implicit, avem o nouă rafinare a definiției 1 (și, de asemenea, profităm de ocazie pentru a renunța la termenul vag de „figură”):

4. Fiecare secțiune netedă a unei curbe închise și netede pe bucăți.

O „curbă închisă” este o curbă care se înfășoară pentru a se întâlni cu ea însăși, astfel încât să nu aibă capete libere. „Lină pe bucățele” înseamnă că este construită din secțiuni netede, care se întâlnesc în puncte neuniforme izolate. Este perfect legitim să dorești să numeri secțiunile netede ale limitei unei astfel de forme și nu este deloc scandalos să folosești cuvântul „parte” atunci când faci acest lucru. Așadar, cu siguranță nu spun că acesta este răspunsul definitiv greșit.

Întrebarea este dacă această interpretare a cuvântului „latură” nu este doar coerentă, ci și suficient de naturală încât să poată fi pur și simplu presupusă fără a fi declarată explicit (ceea ce rareori, dacă nu chiar niciodată, este). Ce se întâmplă atunci când netezimea și rectitudinea se echivalează diferit? Luați în considerare această formă de piatră de mormânt, creată prin înlocuirea vârfului unui pătrat cu un semicerc de diametru egal.

Aceasta are două secțiuni netede (linia de jos și restul), dar trei muchii drepte (plus o bucată curbă care unește lin două dintre ele). Așadar, câte laturi are? Mi-am consultat din nou prietenii de pe Twitter:

De data aceasta ar fi trebuit să includ „infinit de multe” ca opțiune, deși aceasta poate fi absorbită în „Niciuna dintre variantele de mai sus”. Oricine votează că cercul are infinit de multe laturi ar trebui să voteze automat „Niciuna dintre cele de mai sus” aici, cu excepția cazului în care – o avertizare importantă – natura acestei forme indică cititorului o noțiune diferită de „latură”. Faptul că alegerile cele mai populare în aceste două sondaje sunt incompatibile sugerează că acesta ar putea fi cazul (sau cel puțin întărește faptul că apele sunt tulburi).

Deși doi este un răspuns perfect respectabil, compatibil cu definiția 4 de mai sus și cu caracterul unilateral al cercului, nu sunt convins că este în mod definitiv cel corect, sau că trei sau patru sunt categoric greșite. Depinde ce vreți să numărați: secțiuni netede, muchii drepte sau muchii drepte plus ceea ce rămâne apoi, oricare dintre acestea ar putea fi răspunsul pe care îl doriți în funcție de context (mai multe despre acest lucru mai jos). În legătură cu aceasta, nu sunt sigur că numărarea numărului de secțiuni netede corespunde pe deplin intuiției mele cu privire la cuvântul „latură”. La urma urmei, cele două secțiuni drepte ale pietrei de mormânt sunt – cred că este corect să spunem – „pe laturi opuse”. Suntem cu adevărat mulțumiți de faptul că ele fac parte simultan din „aceeași latură”?

Ați putea protesta că am confundat două sensuri diferite ale cuvântului „latură”, că terminologia se ciocnește uneori și că trebuie doar să trăim cu ea. Eu nu sunt atât de sigur, totuși. Ideea acestui exercițiu este de a extrapola pornind de la o situație (figuri rectilinii) în care cele două noțiuni se potrivesc destul de bine. Dacă ar exista o nouă idee care să capteze tot ceea ce ne-a plăcut la original, dar care să se aplice și la o categorie mai largă de forme, atunci aceasta ar avea o pretenție covârșitoare de a fi singurul răspuns corect. Dar dacă toate încercările noastre de generalizare implică sacrificarea unor aspecte dezirabile ale originalului, atunci poate că nu există o singură generalizare corectă. Există alegeri diferite, cu compromisuri diferite, care ar putea fi potrivite în contexte diferite (și dacă ne aflăm într-o situație în care mai multe sunt în joc, atunci ar putea fi util să li se dea nume diferite).

Iată o altă variantă: o piatră de mormânt Weierstrass creată prin înlocuirea marginii superioare a unui pătrat cu o secțiune a funcției Weiestress, o linie infinit ondulată care nu este netedă nicăieri.

Iată (și observați greșeala de tipar) ce au făcut prietenii mei de pe Twitter despre asta – deși mai puțini s-au aventurat să își dea cu părerea:

În ciuda scepticismului urmăritorilor mei de pe Twitter, voi explica într-un minut de ce nu cred că este o prostie să consider că acest lucru are patru laturi (dintre care una nu este netedă). Pe de altă parte, dacă preferați ca laturile să fie netede, atunci aveți din nou de ales între a vedea că are infinit de multe laturi (dintre care trei au lungimea 1, iar restul au lungimea 0), sau că are 3 laturi plus o porțiune de graniță cu siguranță nu este o latură.

Pentru o latură: o singură curbă netedă.
Împotriva unei laturi: aceeași latură pe laturi opuse.

Pe tangentă 3: laturi versus muchii

Câte laturi are un pătrat? Patru. Câte muchii are? Patru. Deci marginile și laturile sunt același lucru? Nu neapărat. Iată două configurații care sunt – cel puțin în mod discutabil – fiecare cu patru laturi, dar care au 5 și respectiv 3 muchii:

De obicei, aș spune că o „muchie” este un obiect topologic, în sensul că funcția sa, nu forma sa, este cea care contează. Gândiți-vă la harta metroului londonez. Dacă ați întreba câte muchii există în acea rețea, nu are niciun merit să totalizați secțiunile drepte sau netede. Contează conexiunile dintre stații (sau vârfuri).

După cum am menționat deja, este obișnuit să ne gândim la un poligon ca la un tip foarte simplu de rețea numit lanț poligonal închis: un șir de vârfuri (în acest caz, colțurile poligonului), legate cu muchii, în așa fel încât fiecare vârf să se afle pe exact două muchii, iar totul să formeze o singură buclă. În această situație, marginile și laturile coincid, la fel ca și vârfurile și colțurile. Dar, în general, puteți rupe această concurență, ca în cele două rețele mici de mai sus.

Dacă doriți să vă gândiți la lucruri din punct de vedere teoretic la rețele, dar vârfurile nu sunt clar marcate, atunci trebuie să ghiciți unde sunt. În cazul unui poligon, acest lucru este ușor – vârfurile se află în colțuri – motiv pentru care trecerea de la o abordare geometrică la una topologică este atât de naturală. Dar cu alte forme, cum ar fi oricare dintre pietrele funerare de mai sus, s-ar putea să nu fie atât de evident. Cu toate acestea, în fiecare caz, dacă vi s-ar spune că există niște vârfuri undeva acolo și vi s-ar cere să le localizați, cred că ar fi rezonabil să ghiciți că sunt patru, și anume colțurile pătratului original, iar muchia de sus a fost reprezentată, din anumite motive, ca o linie care nu este dreaptă. Și dacă vrem să ne gândim la lucrurile în acest fel, cu fiecare dintre pietrele de mormânt având 4 muchii, atunci ar putea părea ciudat (deși coerent din punct de vedere logic!) pentru a insista ca acestea să aibă un alt număr de laturi (mai ales că partea de sus este – în ciuda propriei sale geometrii – în mod clar „pe o parte” a figurii). De fapt, mai degrabă decât să ghicească, unul dintre corespondenții mei de pe Twitter m-a întrebat: „Au fost eliminate ambele vârfuri de sus?”, o întrebare care are sens doar din perspectiva teoriei rețelelor.

Unde rămâne cercul? Problema este că niciun punct de pe cerc nu are o pretenție mai bună de a fi vertex decât oricare altul. Așadar, deși este tentant (și din nou coerent) să privim cercul ca pe o rețea cu o singură muchie, dacă vom insera vârfuri, nu există nici un motiv evident pentru a prefera unul în locul oricărui alt număr.

Am putea să îl privim ca pe o rețea fără niciun vârf, un fel de linie de metrou fără stații? Concepția matematică obișnuită a unei rețele nu ar permite acest lucru, dar acest lucru nu ar trebui să ne descurajeze prea mult. Acest lucru sugerează o abordare pur topologică. Problema este că, din acest punct de vedere, în timp ce un cerc poate fi un fel de rețea fără vârfuri și cu o singură muchie, la fel este și un pătrat (dacă acesta este modul în care este dispusă linia de metrou). În topologie, un pătrat este un cerc. (Acesta nu este un paradox, ci pur și simplu se spune că limita este o singură buclă, a cărei formă nu contează). Așadar, în timp ce acest tip de rețea are „o muchie”, în mod evident, un pătrat nu are „o latură”, astfel încât relația dintre laturi (geometrică) și muchii (topologică) s-a rupt din nou, la fel ca în cele două mici rețele ilustrate mai sus. Așadar, această abordare nu ne duce foarte departe.

Nu există laturi?

Ar putea părea paradoxal să susținem că un cerc (sau orice formă) nu are „laturi”. Dar argumentul de apărare este simplu. Ne întoarcem la definiția 2:

2. Linie dreaptă care face parte din limita unei figuri plane.

Este o frază simplă, ușor de înțeles, care surprinde perfect laturile unui pătrat. Nu am reușit să găsim o generalizare satisfăcătoare a acesteia la figurile curbe, așa că cel mai bine este să rămânem la original. Iar un cerc nu are niciuna.

Pentru că nu are laturi: adevărat, conform unei noțiuni rezonabile de „latură”.
Contra nici o latură: sună ca un koan Zen.

Niciuna din cele de mai sus?

Reamintim definiția furnizată de Google:

3. Fiecare dintre liniile care formează limita unei figuri plane rectilinii.

Tentativa de a aplica acest lucru la un cerc – o figură nerectilinie – nu produce nimic. Întrebarea este la fel de lipsită de sens ca și „Câte laturi are Luni?”

Din moment ce Definiția 3 este cea mai oficială (singura din această postare care nu a fost inventată de mine sau de copiii mei), asta nu face ca „Niciuna dintre variantele de mai sus” să fie categoric răspunsul corect? Poate. Pe de altă parte: atunci când cineva ne pune o întrebare, principiul carității ne cere, poate, să presupunem că aceasta are sens dacă nu putem stabili cu fermitate contrariul, iar definițiile 1, 2, 4 și alte variante fac posibil acest lucru. Mai mult, definiția 3 este mai degrabă lingvistică decât formal matematică și, prin urmare, este mai degrabă descriptivă decât prescriptivă, așa că nu ar trebui să ne ascundem de ea.

Pentru niciuna dintre cele de mai sus: disfuncție semantică.
Împotriva niciuneia dintre cele de mai sus: caritate dialogică.

Răspunsul corect

Ce m-a determinat să scriu această postare? La fel ca nenumărați elevi de școală primară, fiilor mei gemeni de cinci ani – elevii de școală primară menționați la început – li s-a pus recent această întrebare la temele pentru acasă. Unul a optat pentru „1”, iar celălalt pentru „0”, iar eu am încercat să surprind și să dezvolt raționamentul lor mai sus. Cred că ambele răspunsuri sunt pe deplin apărabile – și niciunul nu este definitiv corect.

Atunci, ce ar trebui să faceți dacă vi se pune întrebarea: Câte laturi are un cerc? După părerea mea, răspunsul optim este să te adresezi matematicianului din viața ta pentru a scrie un tratat de 3000 de cuvinte pe această temă, pe care să-l tipărești apoi și să-l înmânezi triumfător nefericitului tău profesor. Dar, în caz contrar, cea mai bună abordare este să urmați exemplul lui Socrate și să răspundeți la întrebare cu o contra-întrebare: Ce înțelegi prin „latură”?

La urma urmei, numărarea până la zero, sau până la unu, sau refuzul de a răspunde la întrebare, nu ne spune practic nimic despre geometria cercurilor. Dar sunt multe de câștigat prin destrămarea noțiunilor familiare, renunțând sau adăugând condiții suplimentare, provocându-ne intuiția prin trecerea de la un context la unul ușor diferit și încercând să scriem cu precizie ce înțelegem printr-un anumit termen într-un anumit context. Despre asta este vorba în adevărata matematică.

Note de subsol

Ați putea face altceva: de exemplu, să alegeți un punct de plecare P pe cerc, de unde să măsurați distanța în jurul circumferinței. Apoi declarați că punctele aflate la o distanță rațională de P sunt colțuri, iar restul sunt laturi. Acest lucru are ca efect obținerea unui număr infinit numărabil de colțuri și a unui număr infinit nenumărabil de laturi. Sau se poate stipula contrariul. Aceasta ar putea fi o potrivire convenabilă pentru abordarea limitei poligonale a cercurilor, dar m-aș strădui să fiu de acord că este suficient de ușor sau de evident pentru a fi considerat „răspunsul corect”.

Unul dintre corespondenții mei de pe Twitter a fost îngrijorat de cât de netedă este curba. Această piatră de mormânt este continuu diferențiabilă, dar nu de două ori așa. Ar fi cu siguranță interesant dacă mulți oameni ar crede că aceasta este o chestiune critică, iar acest lucru ar putea fi probabil testat cu o piatră de mormânt infinit de netedă construită din ceva de genul acesta, deși nu m-am gândit la detalii.

Am putea încerca să formalizăm acest lucru după cum urmează: într-un pătrat (sau orice poligon), o latură are proprietatea că, pornind din orice poziție din interior, puteți tăia forma direct prin locația dvs., astfel încât partea aleasă să fie ferm pe o parte a tăieturii. Acest lucru nu funcționează în cazul pietrei de mormânt cu două fețe: orice tăiere va secționa întotdeauna partea lungă. Am putea slăbi acest lucru spunând că, pentru a fi considerată o latură, trebuie să existe cel puțin o modalitate de a tăia forma astfel încât partea respectivă să se afle pe o parte a tăieturii. Acest lucru ne-ar permite să spunem că piatra de mormânt are patru laturi (chiar dacă secțiunea curbă nu se află de o parte a punctelor din regiunea superioară). În cazul cercului însă, presupusa sa latură nu se află niciodată pe o singură parte (deci ar fi exclusă), și doar secțiunea dreaptă a unui semicerc ar conta ca latură.

Nu este ușor de găsit o justificare riguroasă care să funcționeze pentru ambele pietre de mormânt, dar mă gândesc mai informal în termeni de puncte Schelling: adică locații care ies în evidență ca fiind speciale din motive care ar putea să nu fie ușor de prezis dinainte.

Recunoștințe

Mulțumesc tuturor celor care au participat sau au redistribuit sondajele mele, sau au discutat cu mine pe Twitter.

.