Clasificarea prin analiza discriminantă
Să vedem cum poate fi derivată LDA ca metodă de clasificare supravegheată. Să considerăm o problemă generică de clasificare: O variabilă aleatoare X provine dintr-una din K clase, cu anumite densități de probabilitate f(x) specifice clasei. O regulă discriminantă încearcă să împartă spațiul de date în K regiuni disjuncte care reprezintă toate clasele (imaginați-vă căsuțele de pe o tablă de șah). Cu aceste regiuni, clasificarea prin analiza discriminantă înseamnă pur și simplu că alocăm x clasei j dacă x se află în regiunea j. Întrebarea este atunci: cum știm în ce regiune se încadrează datele x? Firește, Putem urma două reguli de alocare:
- Regula probabilității maxime: Dacă presupunem că fiecare clasă ar putea apărea cu aceeași probabilitate, atunci alocăm x clasei j dacă

- Regula bayesiană: Dacă cunoaștem probabilitățile anterioare ale clasei, π, atunci alocăm x clasei j dacă

Analiza discriminantă liniară și pătratică
Dacă presupunem că datele provin dintr-o distribuție Gaussiană multivariată, i.adică distribuția lui X poate fi caracterizată prin media (μ) și covarianța (Σ), se pot obține forme explicite ale regulilor de alocare de mai sus. Urmând regula Bayesiană, clasificăm datele x în clasa j dacă aceasta are cea mai mare probabilitate dintre toate cele K clase pentru i = 1,…,K:

Funcția de mai sus se numește funcție discriminantă. Observați utilizarea logaritmului verosimilității aici. Într-un alt cuvânt, funcția discriminantă ne spune cât de probabile sunt datele x din fiecare clasă. Prin urmare, limita de decizie care separă oricare două clase, k și l, este setul de x în care două funcții discriminante au aceeași valoare. Prin urmare, orice date care se încadrează pe granița de decizie sunt la fel de probabile din cele două clase (nu am putut decide).
LDA apare în cazul în care presupunem o covarianță egală între K clase. Adică, în loc de o matrice de covarianță pe clasă, toate clasele au aceeași matrice de covarianță. Atunci putem obține următoarea funcție discriminantă:

Observați că aceasta este o funcție liniară în x. Astfel, limita de decizie între orice pereche de clase este, de asemenea, o funcție liniară în x, motiv pentru care se numește: analiză discriminantă liniară. Fără ipoteza de covarianță egală, termenul pătratic din verosimilitate nu se anulează, prin urmare funcția discriminantă rezultată este o funcție pătratică în x:

În acest caz, limita de decizie este pătratică în x. Acest lucru este cunoscut sub numele de analiză discriminantă pătratică (QDA).
Ce este mai bine? LDA sau QDA?
În problemele reale, parametrii populației sunt de obicei necunoscuți și sunt estimați din datele de instruire ca medii ale eșantionului și matrici de covarianță ale eșantionului. În timp ce QDA acomodează limite de decizie mai flexibile în comparație cu LDA, numărul de parametri necesari a fi estimați crește, de asemenea, mai rapid decât cel al LDA. În cazul LDA, sunt necesari (p+1) parametri pentru a construi funcția discriminantă din (2). Pentru o problemă cu K clase, am avea nevoie doar de (K-1) astfel de funcții discriminante prin alegerea arbitrară a unei clase ca fiind clasa de bază (scăzând probabilitatea clasei de bază din toate celelalte clase). Prin urmare, numărul total de parametri estimați pentru LDA este (K-1)(p+1).
Pe de altă parte, pentru fiecare funcție discriminantă QDA din (3), trebuie să se estimeze vectorul mediu, matricea de covarianță și prioritatea clasei:
– Media: p
– Covarianța: p(p+1)/2
– Prioritatea clasei: 1
În mod similar, pentru QDA, trebuie să estimăm parametrii (K-1){p(p+3)/2+1}.
Din acest motiv, numărul de parametri estimați în LDA crește liniar cu p, în timp ce cel din QDA crește pătratic cu p. Ne-am aștepta ca QDA să aibă performanțe mai slabe decât LDA atunci când dimensiunea problemei este mare.
Best of two worlds? Compromis între LDA & QDA
Potem găsi un compromis între LDA și QDA prin regularizarea matricelor de covarianță ale claselor individuale. Regularizarea înseamnă că punem o anumită restricție asupra parametrilor estimați. În acest caz, solicităm ca matricea de covarianță individuală să se micșoreze către o matrice de covarianță comună pusă în comun printr-un parametru de penalizare, de exemplu, α:

Matricea de covarianță comună poate fi, de asemenea, regularizată către o matrice identitate printr-un parametru de penalizare, de exemplu, β:

În situațiile în care numărul variabilelor de intrare depășește cu mult numărul eșantioanelor, matricea de covarianță poate fi prost estimată. Se speră că micșorarea poate îmbunătăți estimarea și precizia clasificării. Acest lucru este ilustrat de figura de mai jos.

Calcul pentru LDA
Potem vedea din (2) și (3) că calculele funcțiilor discriminante pot fi simplificate dacă diagonalizăm mai întâi matricile de covarianță. Adică, datele sunt transformate pentru a avea o matrice de covarianță identică (fără corelație, varianță de 1). În cazul LDA, iată cum procedăm cu calculul:

Pasul 2 sferizează datele pentru a produce o matrice de covarianță identitate în spațiul transformat. Pasul 4 se obține urmând (2).
Să luăm un exemplu cu două clase pentru a vedea ce face cu adevărat LDA. Să presupunem că există două clase, k și l. Clasificăm x în clasa k dacă

Condiția de mai sus înseamnă că este mai probabil ca clasa k să producă date x decât clasa l. Urmând cei patru pași descriși mai sus, scriem
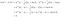
Asta este, clasificăm datele x în clasa k dacă

Regula de alocare derivată dezvăluie funcționarea LDA. Partea stângă (l.h.s.) a ecuației este lungimea proiecției ortogonale a lui x* pe segmentul de dreaptă care unește cele două medii de clasă. Partea dreaptă este locația centrului segmentului corectată de probabilitățile anterioare ale clasei. În esență, LDA clasifică datele sphered în funcție de cea mai apropiată medie de clasă. Putem face aici două observații:
- Punctul de decizie se abate de la punctul central atunci când probabilitățile anterioare ale clasei nu sunt identice, adică limita este împinsă spre clasa cu o probabilitate anterioară mai mică.
- Datele sunt proiectate pe spațiul acoperit de mediile clasei (înmulțirea lui x* și scăderea mediei pe l.h.s. a regulii). Comparațiile de distanță se fac apoi în acest spațiu.
.