De fiecare dată când discutăm despre predicția modelului, este important să înțelegem erorile de predicție (bias și varianță). Există un compromis între capacitatea unui model de a minimiza prejudecata și varianța. Dobândirea unei înțelegeri adecvate a acestor erori ne-ar ajuta nu numai să construim modele precise, ci și să evităm greșeala de supraadaptare și subadaptare.
Așa că haideți să începem cu elementele de bază și să vedem cum acestea fac diferența în modelele noastre de învățare automată.
Ce este bias-ul?
Bias-ul este diferența dintre predicția medie a modelului nostru și valoarea corectă pe care încercăm să o prezicem. Un model cu bias mare acordă foarte puțină atenție datelor de instruire și simplifică prea mult modelul. Întotdeauna conduce la o eroare ridicată pe datele de instruire și de testare.
Ce este varianța?
Varianța este variabilitatea predicției modelului pentru un anumit punct de date sau o valoare care ne indică răspândirea datelor noastre. Modelul cu o varianță mare acordă multă atenție datelor de antrenament și nu generalizează pe datele pe care nu le-a mai văzut înainte. Ca urmare, astfel de modele au performanțe foarte bune pe datele de instruire, dar au rate de eroare ridicate pe datele de testare.
Matematic
Să considerăm variabila pe care încercăm să o prezicem ca fiind Y și alte covariate ca fiind X. Presupunem că există o relație între cele două astfel încât
Y=f(X) + e
Unde e este termenul de eroare și este distribuit în mod normal cu o medie de 0.
Vom face un model f^(X) al lui f(X) folosind regresia liniară sau orice altă tehnică de modelare.
Deci eroarea pătratică așteptată la un punct x este
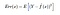
Eroarea pătratică așteptată la un punct x este Err(x) poate fi descompus în continuare ca

Err(x) este suma lui Bias², varianței și a erorii ireductibile.
Eroarea ireductibilă este eroarea care nu poate fi redusă prin crearea unor modele bune. Este o măsură a cantității de zgomot din datele noastre. Aici este important să înțelegem că, indiferent cât de bun facem modelul nostru, datele noastre vor avea o anumită cantitate de zgomot sau eroare ireductibilă care nu poate fi eliminată.
Bias și varianță folosind diagrama ochiului de taur

În diagrama de mai sus, centrul țintei este un model care prezice perfect valorile corecte. Pe măsură ce ne îndepărtăm de țintă, predicțiile noastre devin din ce în ce mai proaste. Putem repeta procesul nostru de construire a modelului pentru a obține lovituri separate asupra țintei.
În învățarea supravegheată, subadaptarea are loc atunci când un model nu reușește să capteze modelul de bază al datelor. Aceste modele au, de obicei, o prejudecată ridicată și o varianță scăzută. Se întâmplă atunci când avem o cantitate foarte mică de date pentru a construi un model precis sau când încercăm să construim un model liniar cu date neliniare. De asemenea, aceste tipuri de modele sunt foarte simple pentru a capta modelele complexe din date, cum ar fi regresia liniară și regresia logistică.
În învățarea supravegheată, supraadaptarea are loc atunci când modelul nostru captează zgomotul împreună cu modelul de bază din date. Se întâmplă atunci când ne antrenăm modelul nostru foarte mult pe seturi de date zgomotoase. Aceste modele au o prejudecată scăzută și o varianță ridicată. Aceste modele sunt foarte complexe, cum ar fi arborii de decizie, care sunt predispuși la supraadaptare.

De ce este compromisul dintre părtinire și varianță?
Dacă modelul nostru este prea simplu și are foarte puțini parametri, atunci poate avea o părtinire mare și o varianță mică. Pe de altă parte, dacă modelul nostru are un număr mare de parametri, atunci va avea o varianță mare și un bias scăzut. Așadar, trebuie să găsim un echilibru corect/bun fără a ne supraadapta și subadapta datele.
Acest compromis în complexitate este motivul pentru care există un compromis între bias și varianță. Un algoritm nu poate fi mai complex și mai puțin complex în același timp.
Eroare totală
Pentru a construi un model bun, trebuie să găsim un echilibru bun între bias și varianță, astfel încât să minimizăm eroarea totală.


Un echilibru optim între părtinire și varianță nu ar fi niciodată supraadaptat sau subadaptat la model.
Din acest motiv, înțelegerea bias-ului și a varianței este esențială pentru înțelegerea comportamentului modelelor de predicție.
Mulțumesc pentru lectură!
.