Mathematics for the Liberal Arts

Het hebben van een constante veranderingssnelheid is het bepalende kenmerk van lineaire groei. Het uitzetten van coördinatenparen die samenhangen met constante verandering zal resulteren in een rechte lijn, de vorm van lineaire groei. In dit deel zullen we een manier formaliseren om lineaire groei te beschrijven met wiskundige termen en concepten. Aan het eind van dit hoofdstuk zul je in staat zijn zowel recursieve als expliciete vergelijkingen te schrijven voor lineaire groei gegeven de beginvoorwaarden, of een constante van verandering. U zult ook het verschil kunnen zien tussen lineaire en geometrische groei aan de hand van een grafiek of een vergelijking.

Lineaire (algebraïsche) groei

voorspellen van groei

Marco is een verzamelaar van antieke frisdrankflessen. Zijn verzameling bestaat momenteel uit 437 flessen. Elk jaar begroot hij genoeg geld om 32 nieuwe flessen te kopen. Kunnen we bepalen hoeveel flessen hij over 5 jaar zal hebben, en hoe lang het zal duren voor zijn verzameling 1000 flessen heeft?

Twee van deze vragen zou je waarschijnlijk zonder vergelijking of formele wiskunde kunnen oplossen, maar we gaan onze benadering van dit probleem formaliseren om een manier te bieden om ingewikkelder vragen te beantwoorden.

Voorstel dat Pn het aantal flessen voorstelt, of de populatie, die Marco na n jaar heeft. Dus P0 staat voor het aantal flessen nu, P1 voor het aantal flessen na 1 jaar, P2 voor het aantal flessen na 2 jaar, enzovoort. We zouden de verandering in Marco’s flessenverzameling kunnen beschrijven met:

P0 = 437

Pn = Pn-1 + 32

Dit heet een recursief verband. Een recursief verband is een formule die de volgende waarde in een reeks relateert aan de vorige waarden. Hier kan het aantal flessen in jaar n worden gevonden door 32 op te tellen bij het aantal flessen in het vorige jaar, Pn-1. Met dit verband kunnen we berekenen:

P1 = P0 + 32 = 437 + 32 = 469

P2 = P1 + 32 = 469 + 32 = 501

P3 = P2 + 32 = 501 + 32 = 533

P4 = P3 + 32 = 533 + 32 = 565

P5 = P4 + 32 = 565 + 32 = 597

We hebben de vraag beantwoord hoeveel flessen Marco over 5 jaar zal hebben.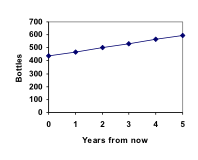

Hoe lang het echter duurt voordat zijn verzameling 1000 flessen heeft bereikt, is nog veel meer rekenwerk nodig.

Hoewel recursieve verbanden uitstekend zijn om eenvoudig en netjes te beschrijven hoe een grootheid verandert, zijn ze niet handig om voorspellingen te doen of problemen op te lossen die zich tot ver in de toekomst uitstrekken. Daarvoor heeft een gesloten of expliciete vorm voor de relatie de voorkeur. Een expliciete vergelijking stelt ons in staat Pn direct te berekenen, zonder dat we Pn-1 hoeven te kennen. Misschien kunt u de expliciete vergelijking al raden, maar laten we die afleiden uit de recursieve formule. We kunnen dit doen door selectief niet te vereenvoudigen als we gaan:

P1 = 437 + 32 = 437 + 1(32)

P2 = P1 + 32 = 437 + 32 + 32 = 437 + 2(32)

P3 = P2 + 32 = (437 + 2(32)) + 32 = 437 + 3(32)

P4 = P3 + 32 = (437 + 3(32)) + 32 = 437 + 4(32)

U kunt nu waarschijnlijk het patroon zien, en veralgemenen dat

Pn = 437 + n(32) = 437 + 32n

Met deze vergelijking kunnen we uitrekenen hoeveel flessen hij na 5 jaar zal hebben:

P5 = 437 + 32(5) = 437 + 160 = 597

We kunnen nu ook oplossen voor wanneer de collectie 1000 flessen zal bereiken door 1000 in te wisselen voor Pn en op te lossen voor n

1000 = 437 + 32n

563 = 32n

n = 563/32 = 17.59

Dus Marco zal 1000 flessen bereiken in 18 jaar.

De stappen van het bepalen van de formule en het oplossen van het probleem van Marco’s flessenverzameling worden in detail uitgelegd in de volgende video’s.

In dit voorbeeld groeide Marco’s verzameling elk jaar met hetzelfde aantal flessen. Deze constante verandering is het kenmerk van lineaire groei. Als we de waarden die we voor Marco’s verzameling hebben berekend uitzetten, zien we dat de waarden een rechte lijn vormen, de vorm van lineaire groei.

Voorbeelden

De populatie elanden in een nationaal bos is in 2003 gemeten op 12.000, en is in 2007 opnieuw gemeten op 15.000. Als de populatie in dit tempo lineair blijft groeien, hoe groot zal de elandenpopulatie dan in 2014 zijn?

Oplossing tonen

Om te beginnen moeten we bepalen hoe we n gaan meten. Bedenk dat P0 de populatie is als n = 0, dus we willen waarschijnlijk niet letterlijk het jaar 0 gebruiken. Aangezien we de bevolking in 2003 al kennen, definiëren we n = 0 als het jaar 2003.

Dan is P0 = 12.000.

Daarna moeten we d vinden. Onthoud dat d de groei per tijdsperiode is, in dit geval de groei per jaar. Tussen de twee metingen groeide de bevolking met 15.000-12.000 = 3.000, maar het duurde 2007-2003 = 4 jaar om zo veel te groeien. Om de groei per jaar te vinden, kunnen we delen: 3000 elanden / 4 jaar = 750 elanden in 1 jaar.

Aternatief kunt u de hellingsformule uit de algebra gebruiken om het gemeenschappelijke verschil te bepalen, waarbij u opmerkt dat de populatie de uitvoer van de formule is, en de tijd de invoer is.

d=slope=\frac{\text{changeinoutput}}{text{changeinput}}=\frac{15.000-12.000}{2007-2003}=\frac{3000}{4}=750

We kunnen nu onze vergelijking schrijven in de vorm die onze voorkeur heeft.

Recursieve vorm

P0 = 12.000

Pn = Pn-1 + 750

Expliciete vorm

Pn = 12.000 + 750(n)

Om de vraag te beantwoorden, moeten we eerst opmerken dat het jaar 2014 n = 11 zal zijn, aangezien 2014 11 jaar na 2003 ligt. De expliciete vorm zal gemakkelijker te gebruiken zijn voor deze berekening:

P11 = 12.000 + 750(11) = 20.250 elanden

Bekijk hier meer over dit voorbeeld.

Het benzineverbruik in de VS is gestaag toegenomen. De verbruiksgegevens van 1992 tot 2004 zijn hieronder weergegeven. Zoek een model voor deze gegevens, en gebruik het om het verbruik in 2016 te voorspellen. Als de trend doorzet, wanneer zal het verbruik dan 200 miljard gallon bereiken?

Jaar	’92	’93	’94	’95	’96	’97	’98	’99	’00	’01	’02	’03	’04
Consumptie (miljard gallons)	110	111	113	116	118	119	123	125	126	128	131	133	136

Oplossing tonen

Plotten van deze gegevens, lijkt het een ongeveer lineair verband te hebben:

Er zijn meer geavanceerde statistische technieken waarmee een vergelijking kan worden gevonden om de gegevens te modelleren, maar om een idee te krijgen van wat er gebeurt, kunnen we een vergelijking vinden door twee stukken van de gegevens te gebruiken – misschien de gegevens van 1993 en 2003.

Als we n = 0 laten overeenkomen met 1993, zou dat P0 = 111 miljard gallon opleveren.

Om d te vinden, moeten we weten hoeveel het gasverbruik elk jaar gemiddeld is toegenomen. Van 1993 tot 2003 is het gasverbruik gestegen van 111 miljard gallon tot 133 miljard gallon, een totale verandering van 133 – 111 = 22 miljard gallon, over 10 jaar. Dit geeft een gemiddelde verandering van 22 miljard gallon / 10 jaar = 2,2 miljard gallon per jaar.

Equivalent,

d=slope=\frac{{text{changeinoutput}}{\text{changeininput}}=\frac{133-111}{10-0}=\frac{22}{10}=2.2 miljard gallons per jaar

We kunnen nu onze vergelijking schrijven in de vorm die onze voorkeur heeft.

Recursieve vorm

P0 = 111

Pn = Pn-1 + 2.2

Expliciete vorm

Pn = 111 + 2,2n

Het berekenen van waarden met behulp van de expliciete vorm en het plotten daarvan met de oorspronkelijke gegevens laat zien hoe goed ons model bij de gegevens past.

We kunnen ons model nu gebruiken om voorspellingen te doen over de toekomst, ervan uitgaande dat de eerdere trend zich ongewijzigd voortzet. Om het benzineverbruik in 2016 te voorspellen:

n = 23 (2016 – 1993 = 23 jaar later)

P23 = 111 + 2,2(23) = 161,6

Ons model voorspelt dat de VS 161.6 miljard gallons benzine in 2016 als de huidige trend zich voortzet.

Om te vinden wanneer het verbruik 200 miljard gallons zal bereiken, zouden we Pn = 200 stellen, en voor n oplossen:

Pn = 200 Vervang Pn door ons model

111 + 2.2n = 200 Trek 111 van beide kanten af

2,2n = 89 Deel beide kanten door 2,2

n = 40,4545

Dit vertelt ons dat de consumptie 200 miljard zal bereiken ongeveer 40 jaar na 1993, dat zou in het jaar 2033 zijn.

De stappen om tot dit antwoord te komen worden in de volgende video in detail beschreven.

De kosten, in dollars, van een lidmaatschap van een sportschool voor n maanden kunnen worden beschreven door de expliciete vergelijking Pn = 70 + 30n. Wat zegt deze vergelijking ons?

Toon oplossing

De waarde voor P0 in deze vergelijking is 70, dus de initiële startkosten zijn 70 dollar. Dit zegt ons dat er een initiatie- of starttarief van $70 moet zijn om lid te worden van de sportschool.

De waarde voor d in de vergelijking is 30, dus de kosten nemen elke maand met $30 toe. Dit vertelt ons dat het maandelijkse lidmaatschapsgeld voor de sportschool $ 30 per maand bedraagt.

De verklaring voor dit voorbeeld wordt hieronder in detail beschreven.

Wanneer goede modellen slecht uitpakken

Bij het gebruik van wiskundige modellen om toekomstig gedrag te voorspellen, is het belangrijk in gedachten te houden dat maar heel weinig trends voor onbepaalde tijd zullen aanhouden.

Exponentiële (Geometrische ) Groei

Bevolkingsgroei

Stel dat elk jaar slechts 10% van de vissen in een meer overlevende nakomelingen heeft. Als er vorig jaar 100 vissen in het meer zaten, zouden er nu 110 vissen zijn. Als er vorig jaar 1000 vissen in het meer zaten, zouden er nu 1100 vissen zijn. Zonder remmende factoren hebben mensen en dieren de neiging om elk jaar met een percentage van de bestaande populatie te groeien.

Stel dat ons meer begon met 1000 vissen, en dat elk jaar 10% van de vissen overlevende nakomelingen heeft. Aangezien we beginnen met 1000 vissen, is P0 = 1000. Hoe berekenen we P1? De nieuwe populatie zal de oude populatie zijn, plus nog eens 10%. Symbolisch:

P1 = P0 + 0.10P0

Merk op dat dit tot een kortere vorm kan worden ingekort door ontbinding in factoren:

P1 = P0 + 0.10P0 = 1P0 + 0.10)P0 = (1+ 0.10)P0 = 1.10P0

Want 10% is het groeipercentage, 1.10 is de groeivermenigvuldigingsfactor. Merk op dat 1,10 kan worden opgevat als “de oorspronkelijke 100% plus nog eens 10%.”

Voor onze vispopulatie,

P1 = 1,10(1000) = 1100

Wij kunnen dan de populatie in latere jaren berekenen:

P2 = 1,10P1 = 1,10(1100) = 1210

P3 = 1,10P2 = 1,10(1210) = 1331

Merk op dat in het eerste jaar de populatie met 100 vissen is toegenomen; in het tweede jaar met 110 vissen; en in het derde jaar met 121 vissen.

Terwijl er sprake is van een constante procentuele groei, neemt de feitelijke toename van het aantal vissen elk jaar toe.

Als we deze waarden in een grafiek zetten, zien we dat deze groei niet helemaal lineair lijkt.

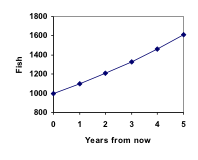
Een walkthrough van dit visscenario kan hier worden bekeken:

Om een beter beeld te krijgen van de invloed van deze procentuele groei, hebben we een expliciete vorm nodig, zodat we snel waarden verder in de toekomst kunnen uitrekenen.

Net als bij het lineaire model gaan we uit van de recursieve vergelijking:

P1 = 1,10(P0 )= 1,10(1000)

P2 = 1,10(P1 )= 1,10(1,10(1000)) = 1,102(1000)

P3 = 1.10(P2 )= 1.10(1.102(1000)) = 1.103(1000)

P4 = 1.10(P3 )= 1.10(1.103(1000)) = 1.104(1000)

Observeren we een patroon, dan kunnen we de expliciete vorm veralgemenen tot:

Pn = 1.10n(1000), of omgekeerd, Pn = 1000(1.10n)

Hieruit kunnen we snel het aantal vissen in 10, 20 of 30 jaar berekenen:

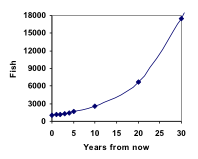
P10 = 1.1010(1000) = 2594

P20 = 1.1020(1000) = 6727

P30 = 1.1030(1000) = 17449

Als we deze waarden bij onze grafiek optellen, zien we een vorm die beslist niet lineair is. Als onze vispopulatie lineair was gegroeid, met 100 vissen per jaar, zou de populatie in 30 jaar slechts 4000 hebben bereikt, vergeleken met bijna 18.000 met deze procentuele groei, exponentiële groei genoemd.

Een video die het expliciete model van dit visverhaal demonstreert, kan hier worden bekeken:

In exponentiële groei groeit de populatie evenredig met de grootte van de populatie, dus als de populatie groter wordt, zal dezelfde procentuele groei een grotere getalsmatige groei opleveren.

Voorbeeld

Tussen 2007 en 2008 groeide Olympia, WA met bijna 3% tot een inwonertal van 245 duizend mensen. Als deze groei doorzet, hoe groot zou het inwonertal van Olympia dan zijn in 2014?

Show Solution

Zoals we al eerder deden, moeten we eerst bepalen welk jaar overeenkomt met n = 0. Omdat we het inwonertal in 2008 kennen, zou het logisch zijn om 2008 te laten corresponderen met n = 0, dus P0 = 245.000. Het jaar 2014 zou dan n = 6 zijn.

We weten dat het groeipercentage 3% is, waardoor r = 0,03.

Gebruik makend van de expliciete vorm:

P6 = (1+0,03)6 (245.000) = 1,19405(245.000) = 292.542,25

Het model voorspelt dat Olympia in 2014 een bevolking van ongeveer 293 duizend mensen zou hebben.

In de volgende video wordt dit voorbeeld in detail uitgelegd.

Evalueren van exponenten op de rekenmachine

Om uitdrukkingen als (1,03)6 te evalueren, is het gemakkelijker om een rekenmachine te gebruiken dan 1,03 zes keer met zichzelf te vermenigvuldigen. De meeste wetenschappelijke rekenmachines hebben een knop voor exponenten. Het is meestal gelabeld als:

^ , yx , of xy .

Om 1,036 te evalueren zouden we 1,03 ^ 6 typen, of 1,03 yx 6. Probeer het maar eens – je zou een antwoord rond 1,1940523 moeten krijgen.

Probeer het

India is het op een na dichtstbevolkte land ter wereld, met een bevolking in 2008 van ongeveer 1,14 miljard mensen. De bevolking groeit elk jaar met ongeveer 1,34%. Als deze trend doorzet, hoe groot zal de Indiase bevolking dan zijn in 2020?

Oplossing tonen

Gebruik makend van n = 0 overeenkomend met 2008, P_12= (1+0,0134)12(1,14) = ongeveer 1.337 miljard mensen in 2020

Voorbeelden

Een vriendin gebruikt de vergelijking Pn = 4600(1.072)n om het jaarlijkse collegegeld van een plaatselijke universiteit te voorspellen. Ze zegt dat de formule is gebaseerd op jaren na 2010. Wat vertelt deze vergelijking ons?

Toon oplossing

In de vergelijking is P0 = 4600, dat is de beginwaarde van het collegegeld wanneer n = 0. Dit vertelt ons dat het collegegeld in 2010 $ 4600 bedroeg.

De groeivermenigvuldiger is 1,072, dus het groeipercentage is 0,072, of 7,2%. Dit vertelt ons dat het collegegeld naar verwachting elk jaar met 7,2% zal groeien.

Wanneer we dit samenvoegen, kunnen we zeggen dat het collegegeld in 2010 $ 4.600 bedroeg, en naar verwachting elk jaar met 7,2% zal groeien.

Bekijk het volgende om dit voorbeeld uitgewerkt te zien.

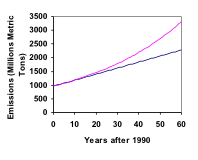
In 1990 was het huishoudelijk energiegebruik in de VS verantwoordelijk voor 962 miljoen ton kooldioxide-uitstoot. In het jaar 2000 was dat aantal gestegen tot 1182 miljoen ton. Als de uitstoot exponentieel toeneemt en in hetzelfde tempo doorgaat, hoe groot zal de uitstoot dan in 2050 zijn?

Toon oplossing

Zoals eerder, corresponderen we n = 0 met 1990, omdat dat het jaar is van de eerste gegevens die we hebben. Dat maakt P0 = 962 (miljoen metrische ton CO2). In dit probleem krijgen we niet het groeipercentage, maar in plaats daarvan dat P10 = 1182.

Wanneer n = 10, ziet de expliciete vergelijking er als volgt uit:

P10 = (1+r)10 P0

We kennen de waarde voor P0, dus die kunnen we in de vergelijking opnemen:

P10 = (1+r)10 962

We weten ook dat P10 = 1182, dus als we dat substitueren, krijgen we

1182 = (1+r)10 962

We kunnen nu deze vergelijking oplossen voor de groeisnelheid, r. Begin met te delen door 962.

Neem de tiende wortel van beide kanten.

r=\sqrt{\frac{1182}{962}}=1+r Trek van beide kanten 1 af.

r=\sqrt{\frac{1182}{962}-1=0,0208 = 2,08%

Dus als de uitstoot exponentieel toeneemt, neemt hij met ongeveer 2,08% per jaar toe. We kunnen nu de uitstoot in 2050 voorspellen door P60 te vinden

P60 = (1+0,0208)60 962 = 3308,4 miljoen ton CO2 in 2050

Bekijk hier meer over dit voorbeeld.

Afronding

Opgemerkt zij dat als we het groeipercentage op 2,1% hadden afgerond, onze berekening voor de emissies in 2050 3347 zou zijn geweest. Afronden op 2% zou ons resultaat hebben veranderd in 3156. Een zeer klein verschil in de groeipercentages wordt sterk vergroot bij exponentiële groei. Daarom wordt aanbevolen het groeipercentage zo weinig mogelijk af te ronden.

Als u moet afronden, houd dan ten minste drie significante cijfers aan – getallen na eventuele voorloopnullen. Dus 0,4162 kan redelijkerwijs worden afgerond tot 0,416. Een groeipercentage van 0,001027 kan redelijkerwijs worden afgerond op 0,00103.

Wortels uitrekenen op de rekenmachine

In het vorige voorbeeld moesten we de tiende wortel van een getal uitrekenen. Dit is anders dan het nemen van de gewone vierkantswortel, √. Veel wetenschappelijke rekenmachines hebben een knop voor algemene wortels. Het label is meestal als volgt:

\sqrt{x}

Om bijvoorbeeld de 3e wortel van 8 te berekenen, typen we ofwel 3 \sqrt{{}} 8, of 8 \sqrt{{}} 3, afhankelijk van de rekenmachine. Probeer het op de jouwe om te zien welke je moet gebruiken – je zou een antwoord van 2 moeten krijgen.

Als je rekenmachine geen algemene wortelknop heeft, is niet alles verloren. Je kunt in plaats daarvan de eigenschap van exponenten gebruiken die stelt dat:

sqrt{a}={a}^{\frac{1}{2}}.

Om de 3e wortel van 8 te berekenen, kun je dus de exponent-toets van je rekenmachine gebruiken om 81/3 te berekenen. Om dit te doen, typt u:

8 yx ( 1 ÷ 3 )

De haakjes vertellen de rekenmachine om 1/3 te delen voordat de exponent wordt gedaan.

Probeer het

Het aantal gebruikers op een sociale netwerksite was 45 duizend in februari toen ze officieel naar de beurs gingen, en groeide tot 60 duizend in oktober. Als de site exponentieel groeit, en de groei gaat in hetzelfde tempo door, hoeveel gebruikers kunnen ze dan verwachten twee jaar nadat ze naar de beurs zijn gegaan?

Toon oplossing

Hier zullen we n meten in maanden in plaats van jaren, waarbij n = 0 overeenkomt met de februari toen ze naar de beurs gingen. Dit geeft P_0= 45 duizend. Oktober is 8 maanden later, dus P_8= 60.
P_8=(1+r)^{8}P_0
60=(1+r)^{8}45
\frac{60}{45}=(1+r)^8
\sqrt{\frac{60}{45}}=1+r
r=\sqrt{\frac{60}{45}}-1=0.0366{ of }3.66%
De algemene expliciete vergelijking is P_n =(1.0366)^{n}45. 24 maanden na de beursgang geeft P_{24}=(1.0366)^{24}45=106,63 duizend gebruikers.

Voorbeeld

Ter vergelijking: wat zou de koolstofuitstoot in 2050 zijn als de uitstoot lineair in hetzelfde tempo toeneemt?

Toon oplossing

Ook hier komt n = 0 overeen met 1990, waardoor P0 = 962. Om d te vinden zouden we dezelfde benadering kunnen gebruiken als eerder, waarbij we opmerken dat de emissies in 10 jaar met 220 miljoen ton zijn toegenomen, wat een gemeenschappelijk verschil geeft van 22 miljoen ton per jaar.

Aternatief zouden we een benadering kunnen gebruiken die vergelijkbaar is met die welke we hebben gebruikt om de exponentiële vergelijking te vinden. Wanneer n = 10, ziet de expliciete lineaire vergelijking er als volgt uit:

P10 = P0 + 10d

We kennen de waarde voor P0, dus kunnen we die in de vergelijking opnemen:

P10 = 962 + 10d

Omdat we weten dat P10 = 1182, krijgen we door dat in te vullen

1182 = 962 + 10d

We kunnen nu deze vergelijking oplossen voor het gemeenschappelijke verschil, d.

1182 – 962 = 10d

220 = 10d

d = 22

Dit vertelt ons dat als de uitstoot lineair verandert, hij elk jaar met 22 miljoen ton toeneemt. Als we de emissies in 2050 voorspellen,

P60 = 962 + 22(60) = 2282 miljoen ton.

U zult merken dat dit getal aanzienlijk kleiner is dan de voorspelling van het exponentiële groeimodel. Het berekenen en plotten van meer waarden helpt om de verschillen te illustreren.

Een demonstratie van dit voorbeeld is te zien in de volgende video.

Dus hoe weten we welk groeimodel we moeten gebruiken wanneer we met gegevens werken? Er zijn twee benaderingen die waar mogelijk samen moeten worden gebruikt:

1. Zoek meer dan twee stukken gegevens. Zet de waarden uit, en zoek naar een trend. Lijkt het alsof de gegevens als een lijn veranderen, of lijken de waarden naar boven te buigen?
2. Beschouw de factoren die bijdragen aan de gegevens. Zijn dat dingen waarvan je zou verwachten dat ze lineair of exponentieel veranderen? In het geval van koolstofemissies bijvoorbeeld, zou men verwachten dat deze, bij afwezigheid van andere factoren, nauw samenhangen met bevolkingsaantallen, die de neiging hebben exponentieel te veranderen.