Quanti lati ha un cerchio?

È una domanda di scuola elementare che causa disaccordo tra i matematici esperti. Per trovare la risposta corretta, ho fatto appello al più rigoroso degli strumenti scientifici, il sondaggio su Twitter:

In retrospettiva mi pento di non aver incluso l’opzione “nessuna delle precedenti”, ma ne riparleremo più avanti. In questo post passerò in rassegna queste tre risposte (e “Nessuna delle precedenti”), e discuterò i loro pro e contro come li vedo io, prima di rivelare drammaticamente la risposta corretta.

Ma prima: perché non possiamo dare direttamente la risposta giusta? Le parole della domanda non sono affatto misteriose. Tutti sappiamo cos’è un “cerchio”, cosa significa contare “quanti” di qualcosa, e cos’è un “lato”… o no? Ecco le definizioni (approssimative) che ho distillato dalle discussioni con due studenti delle scuole elementari che erano stati all’estremità di questa domanda:

1. Una linea che fa parte del confine di una forma di una figura piana.

Lo scopo di dire figura piana piuttosto che “forma” qui è che vogliamo forme che vivono in 2 dimensioni (per esempio quadrati o cerchi, ma non sfere o cubi). La prossima domanda è cosa sia una “linea” nella definizione 1. Ecco una variante che lo precisa:

2. Una linea retta che fa parte del confine di una figura piana.

Se si digita “define: side” in Google, la definizione più rilevante è:

Una figura rettilinea è una figura costruita da linee rette. Quindi questa definizione è un ulteriore perfezionamento della definizione 2, e ci permette di affermare che un quadrato ha quattro lati, ma in apparenza non ha nulla da dire sulle figure piane non rettilinee come i cerchi.

Infinitamente molti lati?

Penso che sia una scommessa sicura che i partecipanti al mio sondaggio su Twitter abbiano un livello di istruzione matematica più alto della media nazionale. Il fatto che si siano divisi su questa domanda, e che una piccola maggioranza abbia scelto una risposta che non è affatto disponibile per il pubblico abituale di questa domanda (gli studenti delle scuole elementari), suggerisce certamente che qualcosa sta andando storto da qualche parte.

Quindi, un cerchio ha infinitamente molti lati? È sicuramente utile considerare un cerchio come il limite dei poligoni con n lati man mano che n diventa sempre più grande. Questo è esattamente l’approccio che Archimede, Liu Hui, e innumerevoli altri hanno usato nel corso dei secoli per studiare la geometria circolare, incluso il trovare approssimazioni per π.

Un’edizione della dinastia Ming del XVI secolo del Jiuzhang suanshu (Nove capitoli sull’arte matematica), terzo secolo dopo Cristo.

A volte è assolutamente sensato, come stenografia conveniente, pensare a un cerchio come a un poligono con infiniti lati.

Ma, da insopportabile pedante matematico, vorrei distinguere tra stenografia conveniente e verità letterale. Se siamo irremovibili sul fatto che un cerchio è davvero un poligono con infiniti lati, allora si pone la domanda: quali sono i lati? E sicuramente l’unica risposta plausibile è: i singoli punti del cerchio. Quanto sono lunghi questi cosiddetti lati? Zero centimetri. E questi lati sono separati da angoli? Apparentemente no, o non ci sono angoli, o ogni punto è sia un lato che un angolo.

Direi che i lati di lunghezza zero sono… un concetto problematico. Come si fa a capire se ne hai? Per esempio, supponiamo che io stia studiando un sistema in cui un quadrato nasce come limite di ottagoni come questo:

In questa situazione, potrebbe avere senso per me pensare al mio quadrato come se avesse otto lati, quattro dei quali hanno lunghezza zero. Ma se dovessi insistere che il mio quadrato (perfettamente ordinario) ha davvero otto lati, potreste alzare un sopracciglio.

Quindi questa – la risposta vincente del mio sondaggio – è l’unica che dichiarerò definitivamente sbagliata, mentre è anche l’unica che offre una qualsiasi intuizione geometrica. Un paradosso? Non proprio. Ragionare per analogia è un’abilità preziosa in matematica e nella vita; allo stesso tempo è importante mantenere la consapevolezza che è quello che stiamo facendo.

Per infiniti lati: geometricamente illuminante.
Per un numero infinito di lati: quadrati a otto lati.

Via sulla tangente 1: apeirogoni

Anche se un cerchio non lo è, esistono poligoni con un numero infinito di lati? Beh, c’è una parola per descrivere una cosa del genere, un apeirogono. Un apeirogono regolare avrebbe quindi lati di lunghezza uguale (non zero) con angoli uguali tra loro. L’unica opzione qui è questo oggetto stupendamente poco eccitante:

Se si obietta che questo è un “poligono” (o a causa degli angoli di 180° o della catena di spigoli che non si chiude in un anello), che ne dite di qualcosa come questo: iniziare alla base di un cerchio, e ad ogni tappa muoversi intorno alla metà di ciò che rimane del cerchio, e sostituire l’arco appena percorso con un bordo dritto:

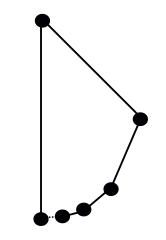
Questo è un vero poligono? Ancora una volta dipende dai vostri termini. Secondo una definizione comune, quella di “catena poligonale chiusa”, questo non si qualifica poiché l’angolo iniziale (in basso a sinistra) si collega solo a uno spigolo. Ma è una mancanza molto vicina: quel punto è il limite di una sequenza di spigoli da destra, rendendo questa forma una “curva chiusa lineare discontinua non autointersecante”, un’altra definizione di poligono che la gente usa.

Se lasciamo il nostro solito mondo euclideo ed entriamo nello spazio iperbolico, allora non c’è ambiguità. Gli apeirogoni (anche gli apeirogoni regolari) semplicemente esistono:

Una piastrellatura del piano iperbolico con apeirogoni regolari. (By Anton Sherwood – Own work, Public Domain, https://commons.wikimedia.org/w/index.php?curid=13260274 )

Off on a tangent 2: extreme points

Potrebbe essere più difendibile dire che un cerchio ha infiniti angoli che infiniti lati (sebbene questa non sia una domanda che sembra essere posta molto spesso). Per cominciare, se un angolo di un quadrato è un punto in cui la sua linea di confine non è dritta, allora ogni punto sul cerchio soddisfa questo. Più sofisticatamente, c’è una nozione di punto estremo di una forma: è qualsiasi punto attraverso il quale si può tracciare un segmento di linea retta che tocca la forma solo in quel punto esatto. Per un quadrato e molte forme familiari i punti estremi coincidono esattamente con gli angoli. Ogni punto sul confine del cerchio è un punto estremo, quindi è certamente vero che un cerchio ne ha infiniti.

Potremmo preoccuparci che alcune forme come questo chevron abbiano angoli che non sono punti estremi:

Qui l’angolo centrale inferiore non è un punto estremo (gli altri tre angoli lo sono). Quello che non va è che questa forma non è convessa (più o meno, ha dei pezzi che sporgono troppo). Un cerchio è convesso, quindi forse non dobbiamo preoccuparci. In alternativa, potremmo rimediare alla situazione definendo un “angolo” come un punto che è un punto estremo o della forma in questione o del suo complemento, cioè l’intero piano con la forma tagliata fuori. Questo approccio individuerebbe gli angoli di tutti i poligoni, compreso il chevron. Per le curve lisce, identificherebbe tutti i punti di confine come “angoli”, tranne i punti di flesso (il che non è irragionevole, dato che lì potremmo sostenere che il confine è dritto).

Un lato?

Nelle scuole elementari, sembra che “uno” sia la risposta che ottiene la spunta. E c’è una giustificazione moderatamente decente. Ricordate la definizione 1 sopra:

1. Una linea che fa parte del confine di una figura piana.

La questione immediata è cosa conta come “linea”, specialmente se non stiamo insistendo sulla rettilineità. Se siamo troppo rilassati su questo punto, allora si potrebbe dire che qualsiasi figura piana ha “un lato”, nello stesso senso in cui ha un confine, un perimetro o una circonferenza. Ma questo deve essere sbagliato, perché sicuramente vogliamo che un quadrato ne abbia quattro. Ebbene, un quadrato ha quattro punti in cui non è liscio, con quattro sezioni lisce in mezzo. Forse erano davvero le sezioni lisce che stavamo contando per tutto il tempo. Così implicitamente abbiamo un nuovo perfezionamento della definizione 1 (e cogliamo anche l’opportunità di liberarci del vago termine “figura”):

4. Ogni sezione liscia di una curva chiusa piecewise-smooth.

Una “curva chiusa” è una che si avvolge su se stessa in modo da non avere estremità libere. “Piecewise-smooth” significa che è costruita da sezioni lisce, che si incontrano in punti isolati non lisci. È perfettamente legittimo voler contare le sezioni lisce del confine di una tale forma, e non è affatto scandaloso usare la parola “lato” quando lo si fa. Quindi non sto certo dicendo che questa sia definitivamente la risposta sbagliata.

La questione è se questa interpretazione di “lato” non sia semplicemente coerente, ma abbastanza naturale da poter essere semplicemente presunta senza essere dichiarata esplicitamente (cosa che raramente o mai è). Cosa succede quando la levigatezza e la rettilineità si sommano in modo diverso? Consideriamo questa forma di lapide, creata sostituendo la parte superiore di un quadrato con un semicerchio di diametro uguale.

Questa ha due sezioni lisce (la linea inferiore e il resto) ma tre bordi dritti (più un pezzo curvo che unisce due di essi in modo liscio). Quindi quanti lati ha? Ho consultato di nuovo i miei amici di Twitter:

Questa volta avrei dovuto includere “infinitamente molti” come opzione, anche se questo può essere assorbito in “Nessuno dei precedenti”. Chiunque voti che il cerchio ha infiniti lati dovrebbe automaticamente votare “Nessuno dei precedenti” qui, a meno che – un avvertimento importante – la natura di questa forma indichi al lettore una diversa nozione di “lato”. Il fatto che le scelte più popolari in questi due sondaggi siano incompatibili suggerisce che questo potrebbe essere il caso (o almeno rafforza che le acque sono torbide).

Anche se due è una risposta perfettamente rispettabile, compatibile con la definizione 4 di cui sopra e con l’unilateralità di un cerchio, non sono soddisfatto che sia definitivamente quella giusta, o che tre o quattro siano categoricamente sbagliati. Dipende da cosa si vuole contare: sezioni lisce, bordi dritti, o bordi dritti più qualsiasi cosa rimanga, ognuno dei quali potrebbe essere la risposta che si desidera a seconda del contesto (più avanti su questo). Relativamente, non sono sicuro che contare il numero di sezioni lisce corrisponda pienamente alla mia intuizione della parola “lato”. Dopo tutto, le due sezioni verticali della lapide sono – penso sia giusto dire – “su lati opposti”. Siamo davvero contenti che facciano parte contemporaneamente dello “stesso lato”?

Potresti protestare che sto confondendo due significati diversi di “lato”, che la terminologia a volte si scontra, e dobbiamo solo conviverci. Non ne sono così sicuro, però. Il punto di questo esercizio è estrapolare da una situazione (figure rettilinee) in cui le due nozioni si sposano abbastanza bene. Se ci fosse una nuova idea che catturasse tutto ciò che ci piaceva dell’originale, ma che si applicasse anche a una categoria più ampia di forme, allora questa avrebbe una pretesa schiacciante di essere l’unica risposta giusta. Ma se tutti i nostri tentativi di generalizzazione implicano il sacrificio di aspetti desiderabili dell’originale, allora forse non esiste un’unica generalizzazione corretta. Ci sono diverse scelte, con diversi compromessi, che potrebbero essere adatti in diversi contesti (e se siamo in una situazione in cui più di uno è in gioco, allora potrebbero essere utilmente dati nomi diversi).

Ecco un’altra variazione: una lapide di Weierstrass creata sostituendo il bordo superiore di un quadrato con una sezione della funzione Weiestress, una linea infinitamente ondulata che non è liscia da nessuna parte.

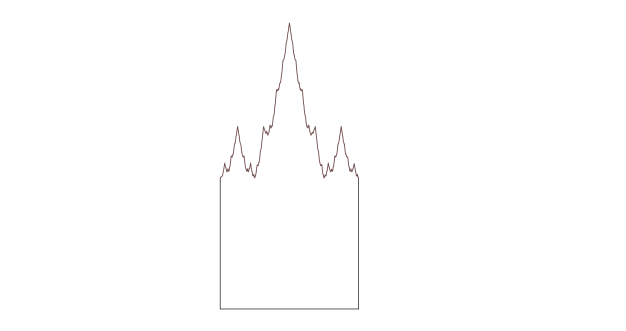
Ecco (e notate il refuso) cosa ne hanno fatto i miei amici di Twitter – anche se pochi si sono fatti un’opinione:

Nonostante lo scetticismo dei miei seguaci di Twitter, spiegherò tra un minuto perché non penso sia sciocco vedere questo come se avesse quattro lati (uno dei quali non liscio). D’altra parte, se preferisci che i tuoi lati siano lisci, allora hai di nuovo una scelta tra vedere che ha infiniti lati (tre dei quali hanno lunghezza 1, e gli altri hanno lunghezza 0), o avere 3 lati più un tratto di confine decisamente non liscio.

Per un lato: un’unica curva liscia.
Contro un lato: lo stesso lato su lati opposti.

Su una tangente 3: lati contro bordi

Quanti lati ha un quadrato? Quattro. Quanti spigoli ha? Quattro. Quindi spigoli e lati sono la stessa cosa? Non necessariamente. Ecco due configurazioni che sono – almeno discutibilmente – ciascuna con quattro lati, ma hanno rispettivamente 5 e 3 spigoli:

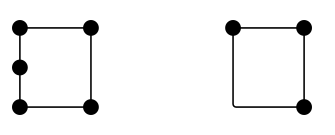
Di solito, direi, uno “spigolo” è un oggetto topologico, nel senso che la sua funzione, non la sua forma, è ciò che conta. Pensate alla mappa della metropolitana di Londra. Se si chiede quanti bordi ci sono in quella rete, non c’è merito nel sommare sezioni dritte o lisce. Sono le connessioni tra le stazioni (o i vertici) che contano.

Come già detto, è comune pensare a un poligono come a un tipo molto semplice di rete chiamata catena poligonale chiusa: una serie di vertici (in questo caso gli angoli del poligono), collegati con spigoli, in modo tale che ogni vertice giaccia esattamente su due spigoli, e il tutto forma un unico anello. In questa situazione spigoli e lati coincidono, così come vertici e angoli. Ma in generale si può rompere questa coincidenza, come nelle due piccole reti di cui sopra.

Se si vuole pensare alle cose in teoria della rete, ma i vertici non sono chiaramente segnati, allora si deve indovinare dove sono. Con un poligono questo è facile – i vertici sono agli angoli – che è il motivo per cui il passaggio tra approcci geometrici e topologici è così naturale. Ma con altre forme, come una delle pietre tombali qui sopra, potrebbe non essere così ovvio. Tuttavia, in ogni caso, se ti dicessero che ci sono dei vertici da qualche parte, e ti chiedessero di localizzarli, penso che sarebbe ragionevole indovinare che ce ne sono quattro, cioè gli angoli del quadrato originale, e che il bordo superiore è stato per qualche motivo rappresentato come una linea non retta. E se vogliamo pensare alle cose in questo modo, con ciascuna delle lapidi che ha 4 bordi, allora potrebbe sembrare strano (anche se logicamente coerente!) per insistere che hanno qualche altro numero di lati (soprattutto perché il lato superiore è – nonostante la sua stessa geometria – chiaramente “su un lato” della figura). Infatti, piuttosto che tirare a indovinare, uno dei miei corrispondenti su Twitter mi ha chiesto “Sono stati rimossi entrambi i vertici superiori?”, una domanda che ha senso solo da una prospettiva teorica della rete.

Dove rimane il cerchio? Il problema è che nessun punto del cerchio ha la pretesa di essere un vertice meglio di qualsiasi altro. Così, anche se è allettante (e di nuovo coerente) vedere un cerchio come una rete con un bordo, se dobbiamo inserire dei vertici, non c’è alcuna ragione ovvia per preferirne uno a qualsiasi altro numero.

Potremmo vederlo come una rete senza alcun vertice, una sorta di linea della metropolitana senza stazioni? La solita concezione matematica di una rete non lo permetterebbe, ma questo non dovrebbe scoraggiarci troppo. Questo suggerisce un approccio puramente topologico. Il problema è che da quel punto di vista, mentre un cerchio può essere una sorta di rete senza vertici e con uno spigolo, lo stesso vale per un quadrato (se è così che la linea della metropolitana è disposta). In topologia, un quadrato è un cerchio. (Questo non è un paradosso, è semplicemente dire che il confine è un singolo anello, la cui forma non ha importanza). Così, mentre questo tipo di rete ha “un bordo”, ovviamente un quadrato non ha “un lato”, quindi la relazione tra lati (geometrica) e bordi (topologica) si è di nuovo interrotta, proprio come nelle due piccole reti illustrate sopra. Quindi questo approccio non ci porta molto avanti.

Nessun lato?

Potrebbe sembrare paradossale sostenere che un cerchio (o qualsiasi forma) non ha “lati”. Ma l’argomento della difesa è semplice. Torniamo alla definizione 2:

2. Una linea retta che fa parte del confine di una figura piana.

Questa è una frase semplice e facilmente comprensibile che cattura perfettamente i lati di un quadrato. Non siamo riusciti a trovare una generalizzazione soddisfacente di questo alle figure curve, quindi la cosa migliore da fare è attenersi all’originale. E un cerchio non ne ha.

Per nessun lato: vero, secondo una nozione sensata di “lato”.
Contro nessun lato: suona come un koan Zen.

Nessuno dei precedenti?

Ricorda la definizione fornita da Google:

3. Ciascuna delle linee che formano il confine di una figura rettilinea piana.

Tentando di applicare questo a un cerchio – una figura non rettilinea – non si ottiene nulla. La domanda è priva di senso come “Quanti lati ha il lunedì?”

Siccome la definizione 3 è la più ufficiale (l’unica in questo post non inventata da me o dai miei figli), questo non rende “Nessuna delle precedenti” categoricamente la risposta giusta? Può darsi. D’altra parte: quando qualcuno ci pone una domanda, il principio di carità forse ci impone di assumere che sia significativa a meno che non possiamo stabilire con certezza il contrario, e le definizioni 1, 2, 4 e altre varianti lo rendono possibile. Inoltre, la definizione 3 è linguistica piuttosto che formalmente matematica, ed è quindi descrittiva piuttosto che prescrittiva, quindi non dovremmo essere vincolati da essa.

Per nessuno dei precedenti: malfunzionamento semantico.
Contro nessuno dei precedenti: carità dialogica.

La risposta giusta

Cosa mi ha spinto a scrivere questo post? Come innumerevoli studenti della scuola primaria, i miei figli gemelli di cinque anni – gli studenti della scuola primaria menzionati all’inizio – sono stati recentemente sottoposti a questa domanda nei loro compiti. Uno ha scelto “1” e l’altro “0”, e ho cercato di catturare ed espandere il loro ragionamento qui sopra. Penso che entrambe le risposte siano del tutto difendibili – e nessuna è definitivamente giusta.

Così, cosa dovresti fare se ti viene posta la domanda: Quanti lati ha un cerchio? Secondo me, la risposta ottimale è rivolgersi al matematico della vostra vita per scrivere un trattato di 3000 parole sull’argomento, che potrete poi stampare e consegnare trionfalmente al vostro sfortunato insegnante. Ma in mancanza di ciò, l’approccio migliore è seguire l’esempio di Socrate e rispondere alla domanda con una contro-domanda: Cosa intendi per “lato”?

In fin dei conti, contare fino a zero, o fino a uno, o rifiutarsi di rispondere alla domanda, non ci dice praticamente nulla sulla geometria dei cerchi. Ma c’è molto da guadagnare smontando nozioni familiari, eliminando o aggiungendo condizioni extra, sfidando la nostra intuizione passando da un contesto a uno leggermente diverso, e cercando di scrivere con precisione cosa intendiamo con un particolare termine in un particolare contesto. Questa è la vera matematica.

Note a piè di pagina

Si potrebbe fare qualcos’altro: ad esempio scegliere un punto di partenza P sul cerchio, da cui misurare la distanza intorno alla circonferenza. Poi dichiarare che i punti a distanza razionale da P sono angoli e il resto sono lati. Questo ha l’effetto di produrre un numero considerevolmente infinito di angoli e un numero considerevolmente infinito di lati. Oppure si potrebbe stabilire il contrario. Questo potrebbe essere un adattamento conveniente per l’approccio al limite poligonale ai cerchi, ma farei fatica a concordare che sia abbastanza facile o ovvio da essere considerato “la risposta giusta”.

Uno dei miei corrispondenti su Twitter era preoccupato di quanto sia liscia la curva. Questa lapide è continuamente differenziabile, ma non due volte. Sarebbe certamente interessante se molte persone pensassero che questa sia una questione critica, e questo potrebbe probabilmente essere testato con una lapide infinitamente liscia costruita da qualcosa di simile, anche se non ho pensato ai dettagli.

Potremmo provare a formalizzare questo come segue: in un quadrato (o qualsiasi poligono), un lato ha la proprietà che partendo da qualsiasi posizione all’interno, puoi tagliare la forma direttamente attraverso la tua posizione, in modo che il lato scelto sia fermamente su un lato del taglio. Questo non funziona per la lapide a due lati: qualsiasi taglio taglierà sempre il lato lungo. Potremmo indebolire questo dicendo che per contare come un lato, ci deve essere almeno un modo di tagliare la forma in modo che il lato sia su un lato del taglio. Questo ci permetterebbe di dire che la lapide ha quattro lati (anche se la sezione curva non è su un lato dei punti nella regione superiore). Per il cerchio però, il suo supposto un lato non è mai su un lato (quindi sarebbe escluso), e solo la sezione dritta di un semicerchio conterebbe come un lato.

Non è facile trovare una giustificazione rigorosa che funzioni per entrambe le lapidi, ma sto pensando più informalmente in termini di punti di Schelling: cioè luoghi che si distinguono come speciali per ragioni che possono non essere facili da prevedere in anticipo.

Riconoscimenti

Grazie a tutti coloro che hanno partecipato o ritwittato i miei sondaggi, o discusso con me su Twitter.