Probabilità > Probabilità Posteriore & la Distribuzione Posteriore
Cos’è la Probabilità Posteriore?
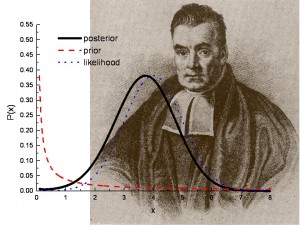
Le probabilità posteriori sono usate nel test di ipotesi bayesiano. Immagine: Los Alamos National Lab.
La probabilità posteriore è la probabilità che un evento accada dopo che tutte le prove o le informazioni di base sono state prese in considerazione. È strettamente correlata alla probabilità anteriore, che è la probabilità che un evento accada prima di prendere in considerazione qualsiasi nuova prova. Si può pensare alla probabilità posteriore come a un aggiustamento della probabilità anteriore:
Per esempio, i dati storici suggeriscono che circa il 60% degli studenti che iniziano il college si laureano entro 6 anni. Questa è la probabilità prioritaria. Tuttavia, voi pensate che questa cifra sia in realtà molto più bassa, quindi andate a raccogliere nuovi dati. Le prove che raccogliete suggeriscono che la cifra vera è in realtà più vicina al 50%; questa è la probabilità posteriore.
Origine dei termini
Le parole posteriore e anteriore vengono dal latino a priori. La definizione di “a priori” è:
“…relativa a ciò che può essere conosciuto attraverso la comprensione di come funzionano certe cose piuttosto che dall’osservazione” ~ Miriam Webster.
L’opposto di “a priori” è a posteriori, che è definito come:
“… relativo a ciò che può essere conosciuto attraverso l’osservazione piuttosto che attraverso la comprensione di come funzionano certe cose” ~ Miriam Webster.
Cos’è una distribuzione posteriore?
La distribuzione posteriore è un modo per riassumere ciò che sappiamo di quantità incerte nell’analisi bayesiana. È una combinazione della distribuzione anteriore e della funzione di verosimiglianza, che vi dice quali informazioni sono contenute nei vostri dati osservati (la “nuova prova”). In altre parole, la distribuzione posteriore riassume ciò che sapete dopo che i dati sono stati osservati. Il riassunto dell’evidenza dalle nuove osservazioni è la funzione di verosimiglianza.
Le distribuzioni posteriori sono di vitale importanza nell’analisi bayesiana. Sono in molti modi l’obiettivo dell’analisi e possono darti:
- Stime di intervallo per i parametri,
- Stime puntuali per i parametri,
- Inferenza di previsione per i dati futuri,
- Valutazioni probabilistiche per la tua ipotesi.
Stephanie Glen. “Probabilità posteriore & la distribuzione posteriore” da StatisticsHowTo.com: Statistica elementare per il resto di noi! https://www.statisticshowto.com/posterior-distribution-probability/
——————————————————————————
Hai bisogno di aiuto per un compito a casa o per un test? Con Chegg Study, puoi ottenere soluzioni passo dopo passo alle tue domande da un esperto del settore. I tuoi primi 30 minuti con un tutor Chegg sono gratuiti!