Introduzione
In informatica, un grafo aciclico diretto (DAG) è un grafo diretto senza cicli. In questo tutorial, mostreremo come fare un ordinamento topologico su un DAG in tempo lineare.
Ordinamento topologico
In molte applicazioni, usiamo i grafi aciclici diretti per indicare le precedenze tra gli eventi. Per esempio, in un problema di programmazione, c’è un insieme di compiti e un insieme di vincoli che specificano l’ordine di questi compiti. Possiamo costruire un DAG per rappresentare i compiti. I bordi diretti del DAG rappresentano l’ordine dei compiti.
Consideriamo un problema su come una persona potrebbe vestirsi per un’occasione formale. Abbiamo bisogno di indossare diversi indumenti, come calze, pantaloni, scarpe, ecc. Alcuni indumenti devono essere indossati prima degli altri. Per esempio, dobbiamo indossare i calzini prima delle scarpe. Alcuni indumenti possono essere messi in qualsiasi ordine, per esempio i calzini e i pantaloni. Possiamo usare un DAG per illustrare questo problema:
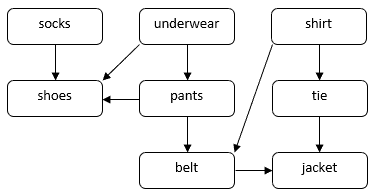
In questo DAG, i vertici corrispondono agli indumenti. Un bordo diretto 
nel DAG indica che dobbiamo mettere l’indumento 
prima dell’indumento 
. Il nostro compito è quello di trovare un ordine per mettere tutti i capi rispettando i vincoli di dipendenza. Per esempio, possiamo mettere gli indumenti nel seguente ordine:
Un ordine topologico di un DAG 
è un ordine lineare di tutti i suoi vertici tale che se contiene un bordo , allora appare prima di nell’ordine. Per un DAG, possiamo costruire un ordinamento topologico con un tempo di esecuzione lineare al numero di vertici più il numero di bordi, che è 
.
Algoritmo di Kahn
In un DAG, ogni percorso tra due vertici ha una lunghezza finita poiché il grafico non contiene un ciclo. Sia 
il percorso più lungo da (vertice sorgente) a (vertice destinazione). Poiché è il percorso più lungo, non ci può essere un bordo in entrata verso . Pertanto, un DAG contiene almeno un vertice che non ha un bordo in entrata.
3.1. Algoritmo di Kahn
Nell’algoritmo di Kahn, costruiamo un ordinamento topologico su un DAG trovando i vertici che non hanno bordi in entrata:
In questo algoritmo, prima calcoliamo i valori di in-degree per tutti i vertici.
Poi, iniziamo con un vertice il cui in-degree è 0 e lo mettiamo alla fine della lista di uscita. Una volta scelto un vertice, aggiorniamo i valori di in-degree dei suoi vertici adiacenti perché il vertice e i suoi bordi in uscita vengono rimossi dal grafico.
Possiamo ripetere il processo di cui sopra fino a scegliere tutti i vertici. La lista di uscita è quindi un ordinamento topologico del grafico.
3.2. Complessità temporale
Per calcolare gli in-degrees di tutti i vertici, dobbiamo visitare tutti i vertici e i bordi di . Pertanto, il tempo di esecuzione è per il calcolo degli in-degree. Per evitare di calcolare nuovamente questi valori, possiamo usare un array per tenere traccia dei valori di in-degree di questi vertici. All’interno del ciclo while, abbiamo anche bisogno di visitare tutti i vertici e i bordi. Pertanto, il tempo di esecuzione complessivo è .
Ricerca in profondità
Possiamo anche usare un algoritmo DFS (Depth First Search) per costruire l’ordinamento topologico.
4.1. Graph DFS with Recursion
Prima di affrontare l’aspetto dell’ordinamento topologico con DFS, iniziamo rivedendo un algoritmo DFS standard ricorsivo:
Nell’algoritmo DFS standard, iniziamo con un vertice casuale in e marchiamo questo vertice come visitato. Poi, chiamiamo ricorsivamente la funzione dfsRecursive per visitare tutti i suoi vertici adiacenti non visitati. In questo modo, possiamo visitare tutti i vertici di in tempo.
Tuttavia, poiché stiamo mettendo ogni vertice nella lista immediatamente quando lo visitiamo, e poiché possiamo iniziare da qualsiasi vertice, l’algoritmo DFS standard non può garantire di generare una lista topologicamente ordinata.
Vediamo cosa dobbiamo fare per affrontare questo difetto.
4.2. Algoritmo di ordinamento topologico basato su DFS
Possiamo modificare l’algoritmo DFS per generare un ordinamento topologico di un DAG. Durante la traversata DFS, dopo che tutti i vicini di un vertice sono stati visitati, lo mettiamo davanti alla lista dei risultati 
. In questo modo, possiamo assicurarci che appaia prima di tutti i suoi vicini nella lista ordinata:
Questo algoritmo è simile all’algoritmo DFS standard. Anche se iniziamo ancora con un vertice casuale, non mettiamo il vertice nella lista immediatamente dopo averlo visitato. Invece, visitiamo prima tutti i suoi vicini ricorsivamente e poi mettiamo il vertice davanti alla lista. Pertanto, se contiene un bordo , allora appare prima di nella lista.
Il tempo di esecuzione complessivo è anche , poiché ha la stessa complessità temporale dell’algoritmo DFS.
Conclusione
In questo articolo, abbiamo mostrato un esempio di ordinamento topologico su un DAG. Inoltre, abbiamo discusso due algoritmi che possono fare un ordinamento topologico in tempo.
L’implementazione Java dell’algoritmo di ordinamento topologico basato su DFS è disponibile nel nostro articolo su Depth First Search in Java.