Ritorna all’indice delle lezioni | Fai le lezioni in ordine | Pagina facile da stampare
Matrix Row Operations (pagina 1 di 2)
“Operations” è il matematico-ese per “procedure”. Le quattro “operazioni di base” sui numeri sono addizione, sottrazione, moltiplicazione e divisione. Per le matrici, ci sono tre operazioni di base sulle righe; cioè, ci sono tre procedure che si possono fare con le righe di una matrice.
La prima operazione è il cambio di riga. Per esempio, data la matrice:

…puoi scambiare le righe per mettere la matrice in una disposizione più bella, come questa:
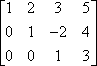
Lo scambio di righe è spesso indicato disegnando delle frecce, come questa:

Quando scambi le righe, stai attento a copiare correttamente le voci.
La seconda operazione è la moltiplicazione di riga. Per esempio, data la seguente matrice:

…puoi moltiplicare la prima riga per -1 per ottenere un valore iniziale positivo nella prima riga:
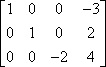
Questa moltiplicazione di riga è spesso indicata usando una freccia con la moltiplicazione elencata sopra, come questa:
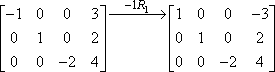
Il “-1R1” indica l’effettiva operazione. Il “-1″ dice che abbiamo moltiplicato per uno negativo; l'”R1” dice che stavamo lavorando con la prima riga. Notate che la seconda e la terza riga sono state copiate giù, invariate, nella seconda matrice. La moltiplicazione è stata applicata solo alla prima riga, quindi le voci per le altre due righe sono state semplicemente trasportate senza modifiche.
Puoi moltiplicare per qualsiasi cosa tu voglia. Per esempio, per ottenere un 1 iniziale nella terza riga della matrice precedente, puoi moltiplicare la terza riga per un mezzo negativo:

Siccome non stavi facendo nulla con la prima e la seconda riga, quelle voci sono state semplicemente copiate senza modifiche nella nuova matrice.
Puoi fare più di una moltiplicazione di riga all’interno dello stesso passo, quindi avresti potuto fare i due passi precedenti in un solo passo, come questo:
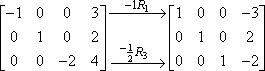
È una buona idea usare una qualche forma di notazione (come le frecce e i pedici di cui sopra) così puoi tenere traccia del tuo lavoro. Le matrici sono molto disordinate, specialmente se le stai facendo a mano, e le note possono rendere più facile controllare il tuo lavoro in seguito. Impressionerà anche il tuo insegnante.
L’ultima operazione di riga è l’addizione di riga. L’addizione di riga è simile al metodo di “addizione” per risolvere sistemi di equazioni lineari. Supponiamo che tu abbia il seguente sistema di equazioni:
x + 3y = 1
-x + y = 3 Copyright © Elizabeth Stapel 2003-2011 All Rights Reserved
Advertisement
Puoi iniziare a risolvere questo sistema sommando le colonne per ottenere 4y = 4:
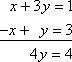
Puoi fare qualcosa di simile con le matrici.Per esempio, data la seguente matrice:

…si può “ridurre” (ottenere più zeri iniziali) la seconda riga aggiungendovi la prima riga (l’obiettivo generale con le matrici in questa fase è di ottenere un “1” – o “0” e poi un “1” – all’inizio di ogni riga della matrice). Quando stavi riducendo il sistema lineare a due equazioni aggiungendo, hai disegnato una barra “uguale” attraverso il fondo e hai aggiunto verso il basso. Quando usi l’addizione su una matrice, avrai bisogno di prendere dei fogli di carta, perché non vuoi provare a fare il lavoro all’interno della matrice. Quindi aggiungi le due righe sul tuo gratta e vinci:
|
Lavoro di gratta e vinci – |
|
Questa è la tua nuova seconda riga; la scriverai al posto della vecchia seconda riga. Il risultato sarà come questo:
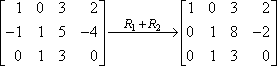
In questo caso, “R1 + R2” sulla freccia significa “ho aggiunto la riga uno alla riga due, e questo è il risultato che ho ottenuto”. Dato che la riga uno non è cambiata, e dato che non abbiamo fatto nulla con la riga tre, queste righe vengono copiate nella nuova matrice senza modifiche.
Top | 1 | 2 | Return to Index Next >>
|
Cita questo articolo come: |
Stapel, Elizabeth. “Operazioni di riga della matrice”. Purplemath. Disponibile da 2016
|