Classificazione tramite analisi discriminante
Vediamo come LDA può essere derivato come metodo di classificazione supervisionata. Consideriamo un generico problema di classificazione: una variabile casuale X proviene da una delle classi K, con alcune densità di probabilità specifiche della classe f(x). Una regola discriminante cerca di dividere lo spazio dei dati in K regioni disgiunte che rappresentano tutte le classi (immaginate le caselle di una scacchiera). Con queste regioni, la classificazione mediante analisi discriminante significa semplicemente che assegniamo x alla classe j se x si trova nella regione j. La domanda è quindi: come facciamo a sapere in quale regione cadono i dati x? Naturalmente, possiamo seguire due regole di assegnazione:
- Regola della massima verosimiglianza: se assumiamo che ogni classe possa verificarsi con uguale probabilità, allora assegniamo x alla classe j se

- Regola Bayesiana: Se conosciamo le probabilità anteriori della classe, π, allora assegniamo x alla classe j se

Analisi discriminante lineare e quadratica
Se assumiamo che i dati provengano da una distribuzione gaussiana multivariata, cioè.Cioè la distribuzione di X può essere caratterizzata dalla sua media (μ) e covarianza (Σ), si possono ottenere forme esplicite delle regole di allocazione di cui sopra. Seguendo la regola Bayesiana, classifichiamo il dato x alla classe j se ha la più alta probabilità tra tutte le classi K per i = 1,…,K:

La funzione sopra è chiamata funzione discriminante. Notate l’uso di log-likelihood qui. In altre parole, la funzione discriminante ci dice quanto è probabile che i dati x appartengano a ciascuna classe. Il confine decisionale che separa due classi qualsiasi, k e l, quindi, è l’insieme di x dove due funzioni discriminanti hanno lo stesso valore. Pertanto, ogni dato che cade sul confine decisionale è ugualmente probabile dalle due classi (non potremmo decidere).
LDA si presenta nel caso in cui assumiamo un’uguale covarianza tra K classi. Cioè, invece di una matrice di covarianza per classe, tutte le classi hanno la stessa matrice di covarianza. Allora possiamo ottenere la seguente funzione discriminante:

Notare che questa è una funzione lineare in x. Così, il confine decisionale tra qualsiasi coppia di classi è anche una funzione lineare in x, il motivo del suo nome: analisi discriminante lineare. Senza l’assunzione di uguale covarianza, il termine quadratico nella probabilità non si annulla, quindi la funzione discriminante risultante è una funzione quadratica in x:

In questo caso, il confine di decisione è quadratico in x. Questo è noto come analisi discriminante quadratica (QDA).
Che cosa è meglio? LDA o QDA?
Nei problemi reali, i parametri della popolazione sono solitamente sconosciuti e stimati dai dati di addestramento come le medie del campione e le matrici di covarianza del campione. Mentre QDA accoglie confini decisionali più flessibili rispetto a LDA, il numero di parametri da stimare aumenta più velocemente di quello di LDA. Per LDA, (p+1) parametri sono necessari per costruire la funzione discriminante in (2). Per un problema con K classi, avremmo solo bisogno di (K-1) tali funzioni discriminanti scegliendo arbitrariamente una classe come classe base (sottraendo la probabilità della classe base da tutte le altre classi). Quindi, il numero totale di parametri stimati per LDA è (K-1)(p+1).
D’altra parte, per ogni funzione discriminante QDA in (3), devono essere stimati il vettore medio, la matrice di covarianza e il priore di classe:
– Media: p
– Covarianza: p(p+1)/2
– Priorità di classe: 1
Similmente, per QDA, dobbiamo stimare (K-1){p(p+3)/2+1} parametri.
Pertanto, il numero di parametri stimati in LDA aumenta linearmente con p mentre quello di QDA aumenta quadraticamente con p. Ci aspettiamo che QDA abbia prestazioni peggiori di LDA quando la dimensione del problema è grande.
Il meglio dei due mondi? Compromesso tra LDA & QDA
Possiamo trovare un compromesso tra LDA e QDA regolarizzando le matrici di covarianza delle singole classi. Regolarizzazione significa che mettiamo una certa restrizione sui parametri stimati. In questo caso, richiediamo che la matrice di covarianza individuale si restringa verso una matrice di covarianza comune messa in comune attraverso un parametro di penalità, ad esempio, α:

La matrice di covarianza comune può anche essere regolarizzata verso una matrice di identità attraverso un parametro di penalità, ad esempio, β:

In situazioni in cui il numero di variabili di input supera notevolmente il numero di campioni, la matrice di covarianza può essere stimata male. Il restringimento può sperare di migliorare la stima e l’accuratezza della classificazione. Questo è illustrato dalla figura seguente.

Computazione per LDA
Possiamo vedere da (2) e (3) che i calcoli delle funzioni discriminanti possono essere semplificati se prima diagonalizziamo le matrici di covarianza. Cioè, i dati vengono trasformati per avere una matrice di covarianza identica (nessuna correlazione, varianza di 1). Nel caso di LDA, ecco come procediamo con il calcolo:

Il passo 2 sferifica i dati per produrre una matrice di covarianza identità nello spazio trasformato. Il passo 4 si ottiene seguendo la (2).
Prendiamo un esempio di due classi per vedere cosa fa realmente LDA. Supponiamo che ci siano due classi, k e l. Classifichiamo x alla classe k se

La condizione precedente significa che la classe k ha più probabilità di produrre dati x rispetto alla classe l. Seguendo i quattro passi sopra descritti, scriviamo
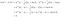
Ovvero, classifichiamo i dati x alla classe k se

La regola di assegnazione derivata rivela il funzionamento di LDA. Il lato sinistro (l.h.s.) dell’equazione è la lunghezza della proiezione ortogonale di x* sul segmento di linea che unisce le due classi medie. Il lato destro è la posizione del centro del segmento corretto dalle probabilità precedenti della classe. Essenzialmente, LDA classifica i dati sferici alla media di classe più vicina. Possiamo fare due osservazioni qui:
- Il punto di decisione si discosta dal punto centrale quando le probabilità anteriori di classe non sono le stesse, cioè il confine è spinto verso la classe con una probabilità anteriore minore.
- I dati sono proiettati nello spazio attraversato dalle medie di classe (la moltiplicazione di x* e la sottrazione della media sull’asse longitudinale della regola). I confronti di distanza sono poi fatti in quello spazio.