Prequisito – Fondamenti di teoria dei grafi – Set 1
Un grafo è una struttura che corrisponde a un insieme di oggetti in cui alcune coppie di oggetti sono in un certo senso “correlate”. Gli oggetti del grafico corrispondono ai vertici e le relazioni tra loro corrispondono ai bordi. Un grafo è rappresentato diagrammaticamente come un insieme di punti che rappresentano i vertici collegati da linee o curve che rappresentano i bordi.
Formalmente,
“Un grafico 
consiste di 
, un insieme non vuoto di vertici (o nodi) e 
, un insieme di bordi. Ogni bordo ha uno o due vertici associati ad esso, chiamati punti finali.”
Tipi di grafi: Ci sono diversi tipi di grafi che si distinguono sulla base dei bordi, la loro direzione, il loro peso, ecc.
1. Grafico semplice – Un grafico in cui ogni bordo collega due diversi vertici e dove non ci sono due bordi che collegano la stessa coppia di vertici è chiamato un grafico semplice. Per esempio, si consideri il seguente grafico –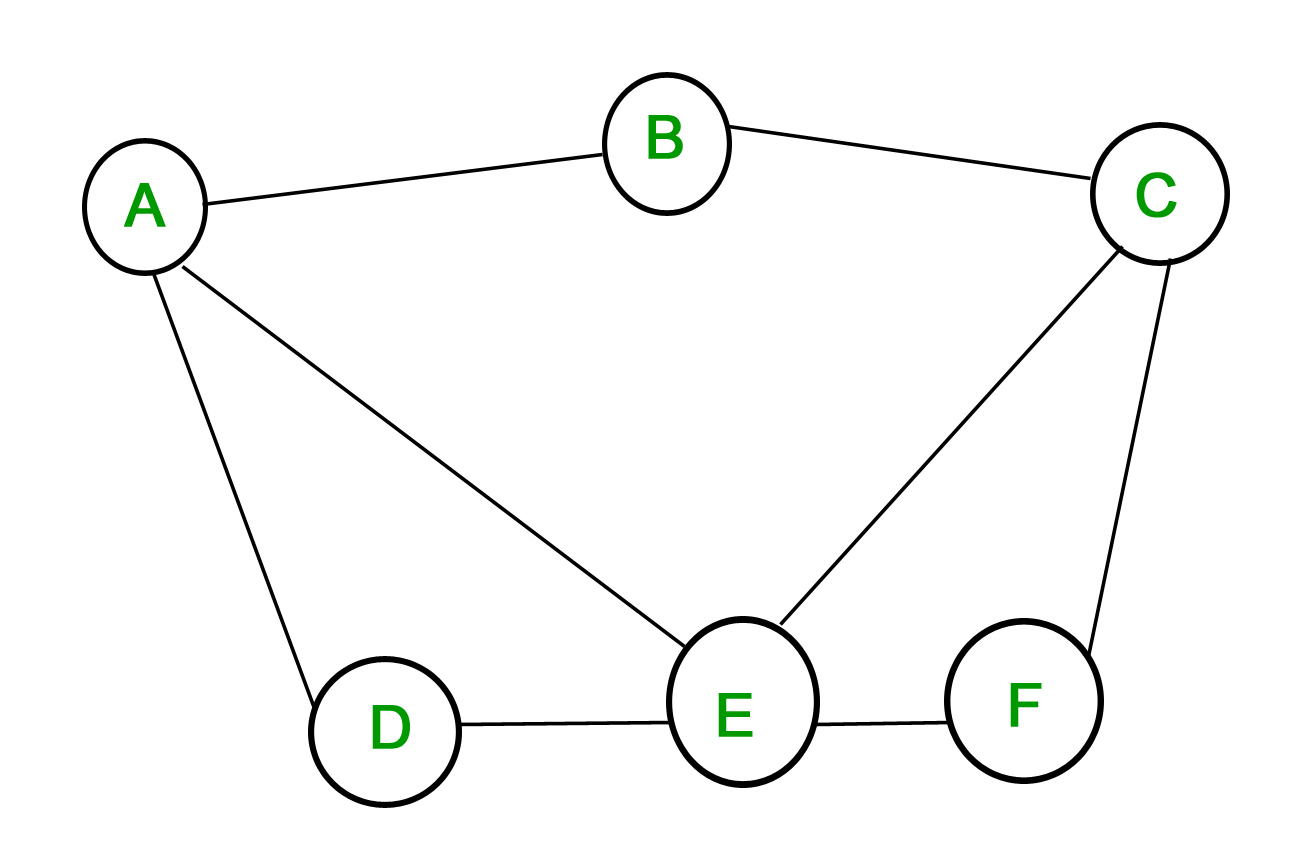
Il grafico di cui sopra è un grafico semplice, poiché nessun vertice ha un self-loop e nessun due vertici hanno più di un bordo che li collega.
I bordi sono denotati dai vertici che collegano- 
è il bordo che collega i vertici 
e 
.
2. Multigrafo – Un grafico in cui più bordi possono collegare la stessa coppia di vertici è chiamato multigrafo.
Siccome ci possono essere più bordi tra la stessa coppia di vertici, la molteplicità del bordo indica il numero di bordi tra due vertici.
Il grafico sopra è un multigrafo poiché ci sono più bordi tra e 
. La molteplicità del bordo 
è 2.
In alcuni grafi, diversamente da quello mostrato sopra, i bordi sono diretti. Questo significa che la relazione tra gli oggetti è solo unidirezionale e non bidirezionale. La direzione dei bordi può essere importante in alcune applicazioni.
In base al fatto che i bordi siano diretti o meno possiamo avere grafi diretti e non diretti. Questa proprietà può essere estesa ai grafi semplici e ai multigrafi per ottenere grafi semplici diretti o non diretti e multigrafi diretti o non diretti.
Terminologia di base dei grafi :
Nella discussione precedente sono già stati spiegati alcuni termini riguardanti i grafi come vertici, bordi, bordi diretti e indiretti ecc. Ci sono altri termini che descrivono le proprietà dei vertici e dei bordi.
- Adiacenza – In un grafico
due vertici 
e 
si dicono adiacenti se sono i punti finali di un bordo. Il bordo 
si dice che è incidente con i vertici.
Nel caso in cui il bordo sia diretto, si dice che è adiacente a e si dice che è adiacente a . Qui, si dice che è il vertice iniziale e si dice che è il vertice terminale. - Grado – Il grado di un vertice è il numero di spigoli incidenti con esso, tranne l’autociclo che contribuisce due volte al grado del vertice. Il grado di un vertice è indicato come
.
Nel caso di grafi diretti, il grado è ulteriormente classificato come in-degree e out-degree. L’in-degree di un vertice è il numero di bordi con il vertice dato come vertice terminale. L’out-degree di un vertice è il numero di bordi con il vertice dato come vertice iniziale. L’in-degree è indicato come
e l’out-degree come 
.
Per esempio nel grafico diretto mostrato sopra che rappresenta i voli tra le città, l’in-degree del vertice “Delhi” è 3 e il suo out-degree è anche 3.
Nota: Se un vertice ha grado zero, è detto isolato. Se il grado è uno, allora si chiama pendente.
Teorema della stretta di mano :
Cosa si ottiene se si sommano i gradi di tutti i vertici di un grafico. Nel caso di un grafo indiretto, ogni bordo contribuisce due volte, una volta per il suo vertice iniziale e la seconda per il suo vertice terminale. Quindi la somma dei gradi è uguale al doppio del numero di bordi. Questo fatto è affermato nel teorema di handshaking.
Let be an undirected graph with edges. ThenIn case G is a directed graph,
Il teorema di handshaking, per i grafi indiretti, ha un risultato interessante –
An undirected graph has an even number of vertices of odd degree.
Prova: Sia 
e 
l’insieme dei vertici di grado pari e dispari rispettivamente.
Sappiamo dal teorema della stretta di mano che,
Quindi,
la somma dei gradi dei vertici con gradi pari è pari. Anche il LHS è pari, il che significa che la somma dei gradi dei vertici con gradi dispari deve essere pari.
Quindi, il numero di vertici con grado dispari è pari.
Alcuni grafi semplici speciali :
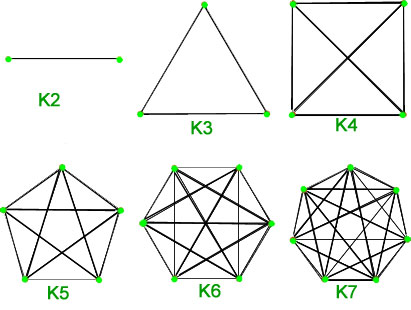
1. Grafi completi – Un grafo semplice di 
vertici che ha esattamente un bordo tra ogni coppia di vertici è chiamato un grafo completo. Un grafo completo di vertici è indicato con 
. Il numero totale di bordi è n*(n-1)/2 con n vertici nel grafo completo.
2. Cicli – I cicli sono grafi semplici con vertici 
e bordi 
. Un ciclo con vertici è indicato come 
. Il numero totale di bordi è n con n vertici nel grafo del ciclo.
3. Ruote – Una ruota è proprio come un ciclo, con un vertice in più che è collegato ad ogni altro vertice. Ruote di vertici con 1 vertice aggiunto sono denotate da 
. Il numero totale di bordi è 2*(n-1) con n vertici nel grafico a ruota.
4. Ipercubo – L’ipercubo o n-cubo è un grafico con 
vertici ognuno rappresentato da una stringa di n bit. I vertici che differiscono al massimo di 1 bit sono collegati da spigoli. Un ipercubo di vertici è indicato con 
. Il numero totale di bordi è n*
con vertici nel grafico cubo.
5. Grafi bipartiti – Un grafico semplice si dice bipartito se il suo insieme di vertici può essere diviso in due insiemi disgiunti tali che ogni bordo in ha il suo vertice iniziale nel primo insieme e il vertice terminale nel secondo insieme. Il numero totale di bordi è (n*m) con (n+m) vertici nel grafo bipartito.
Teorema – Un grafo semplice è bipartito se e solo se è possibile assegnare uno di due
colori diversi ad ogni vertice del grafo in modo che a due adiacenti non sia assegnato lo stesso
colore.
Un grafo bipartito con 
e vertici nei suoi due sottoinsiemi disgiunti si dice completo se esiste un bordo da ogni vertice del primo insieme a ogni vertice del secondo insieme, per un totale di 
bordi. Un grafo bipartito completo con vertici nel primo insieme e vertici nel secondo insieme è indicato come 
.
Domande angolari GATE CS
Praticare le seguenti domande ti aiuterà a verificare le tue conoscenze. Tutte le domande sono state poste in GATE negli anni precedenti o nei GATE Mock Tests. Si consiglia vivamente di praticarle.
1. GATE CS 2013, Domanda 25
2. GATE CS 2014 Set-1, Domanda 61
3. GATE CS 2006, Domanda 71
4. GATE CS 2002, Domanda 25
5. GATE CS 2004, Domanda 37
6. GATE CS 2014 Set-2, Domanda 13
Riferimenti-
Graphs – Wikipedia
Matematica discreta e le sue applicazioni, di Kenneth H Rosen
Questo articolo è stato contribuito da Chirag Manwani. Se ti piace GeeksforGeeks e vuoi contribuire, puoi anche scrivere un articolo usando contribute.geeksforgeeks.org o inviare il tuo articolo a [email protected]. Vedi il tuo articolo apparire sulla pagina principale di GeeksforGeeks e aiuta altri Geeks.