La diffrazione dei raggi X è una tecnica comune di caratterizzazione dei materiali che permette di identificare gli orientamenti dei cristalli e la spaziatura interatomica. I raggi X sono usati per questo perché la lunghezza d’onda è sulla stessa scala di lunghezza della spaziatura interatomica e dei valori dei parametri del reticolo.
Cosa succede?
Un raggio X è generato in un tubo a vuoto riscaldando un filamento di tungsteno oltre la sua funzione di lavoro per espellere gli elettroni. Le condizioni di vuoto sono necessarie per aumentare il percorso libero medio degli elettroni. Gli elettroni sono accelerati in un catodo di rame con un’energia dell’ordine di 25 keV. Le collisioni degli elettroni con il catodo di rame provocano ionizzazioni del guscio interno, producendo raggi X quando gli elettroni ad alta energia cadono per riempire il vuoto a bassa energia. Gli elettroni di vari livelli di energia superiore cadono, producendo onde elettromagnetiche di energia variabile. Così, vengono generati raggi x di lunghezze d’onda multiple (di tipo K-beta e K-alfa). Per la diffrazione dei raggi X, è ideale avere una luce monocromatica che interagisce con il campione, quindi i raggi X K-beta vengono filtrati con una piastra di nichel. Anche se ci sono effettivamente due energie K-alfa associate, le energie sono così simili che non influenzano significativamente il profilo complessivo del picco. I raggi x passano attraverso un collimatore per regolare la larghezza del fascio.
Un po’ di background con la legge di Bragg
La legge di Bragg descrive la relazione per l’interferenza costruttiva, dove i raggi x di lunghezza d’onda λ incidenti sul materiale con un angolo θ sono diffratti da piani di cristallo separati dalla distanza d e n rappresenta un intero.
Come mostrato qui sotto, uno spostamento di fase nell’onda causa un’interferenza costruttiva, come mostrato a sinistra, o un’interferenza distruttiva, rappresentata a destra, secondo l’angolo 2θ.
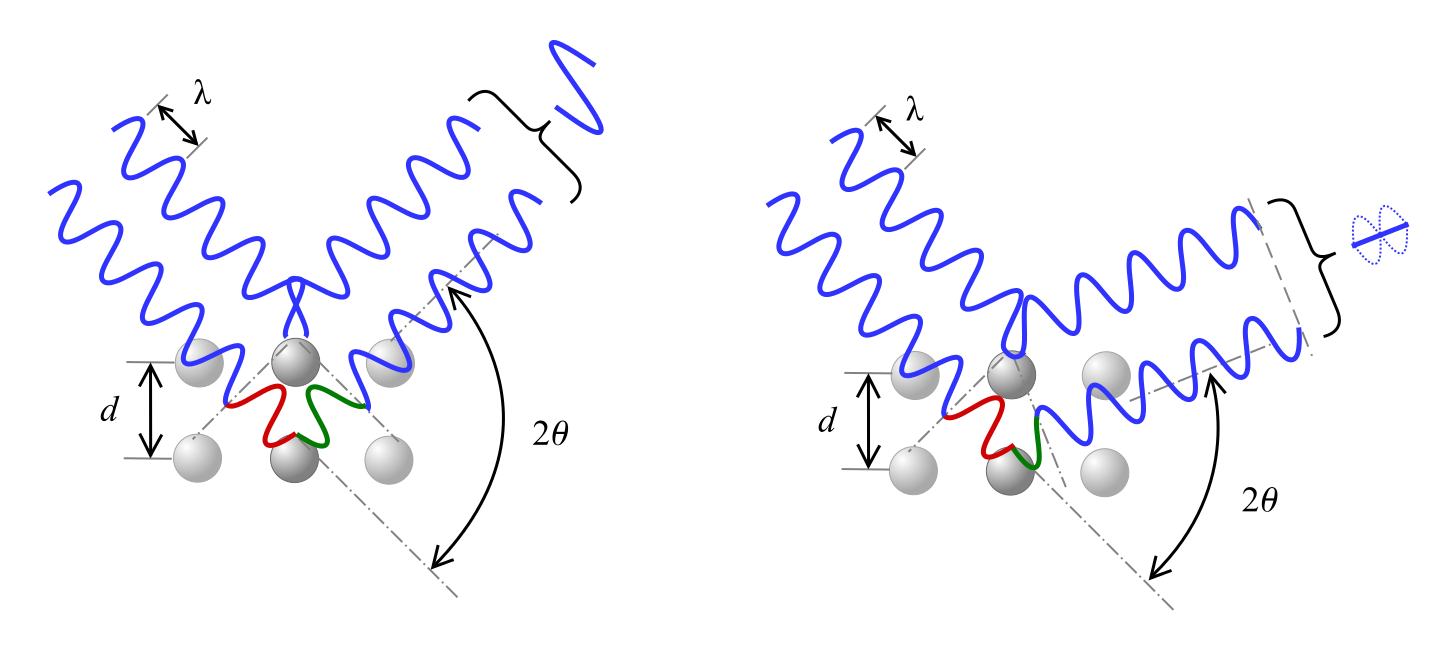
Equazioni per l’interpretazione dei risultati XRD
Il contatore, visto sotto in uno schema di un diffrattometro a raggi X, viene ruotato su una gamma di valori 2θ e registra l’intensità del segnale dei raggi X riflesso dal cristallo in ogni posizione. Questa intensità misurata in funzione di 2θ è usata per generare un profilo di picco.
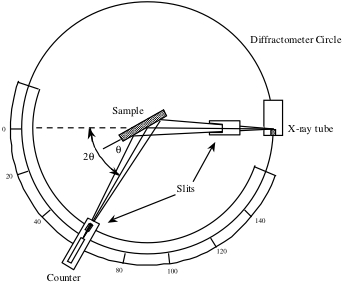
Per gli angoli che soddisfano la condizione di Bragg, si osserverà un picco nel segnale dei raggi X dovuto all’interferenza costruttiva. Questi picchi sono poi usati per identificare le direzioni del cristallo e calcolare i parametri del reticolo. Per i sistemi cubici, la spaziatura interplanare, d, può essere calcolata dalla seguente equazione derivata dalla geometria del cristallo, dove a è il parametro del reticolo e h, k, e l sono gli indici di Miller.
Combinando la legge di Bragg e la spaziatura interplanare si ottiene la seguente equazione.
Qui abbiamo spostato tutte le costanti sul lato sinistro dell’equazione, permettendoci di confrontare i rapporti dei valori di sin2(θ) e degli indici di Miller tra i diversi picchi.
Quando l’onda elettromagnetica incidente colpisce il materiale del campione, gli elettroni che risiedono nel materiale vengono perturbati in un modello oscillante, che genera nuovi raggi X e disperde efficacemente le onde luminose incidenti. Si verificano due tipi di dispersione: la dispersione coerente o elastica coinvolge elettroni oscillanti strettamente legati che disperdono i raggi X della stessa lunghezza d’onda, e la dispersione incoerente che si verifica quando gli elettroni vagamente legati sono messi in movimento oscillatorio e generano raggi X di energia diversa. La diffrazione dei raggi X misura l’intensità dei raggi X sparsi in modo coerente, che raggiunge i picchi dove le onde interferiscono costruttivamente. Il fattore di diffusione atomica può essere definito come un rapporto tra l’ampiezza dell’onda diffusa da un atomo diviso per l’ampiezza dell’onda diffusa da un singolo elettrone. Questo rapporto descrive essenzialmente l’efficienza di diffusione di un atomo per una data direzione.
Esempio di dati XRD
Ecco i dati raccolti da un esperimento che ho fatto durante il mio corso di laboratorio universitario cercando di identificare un metallo sconosciuto basato sulla sua struttura cristallina.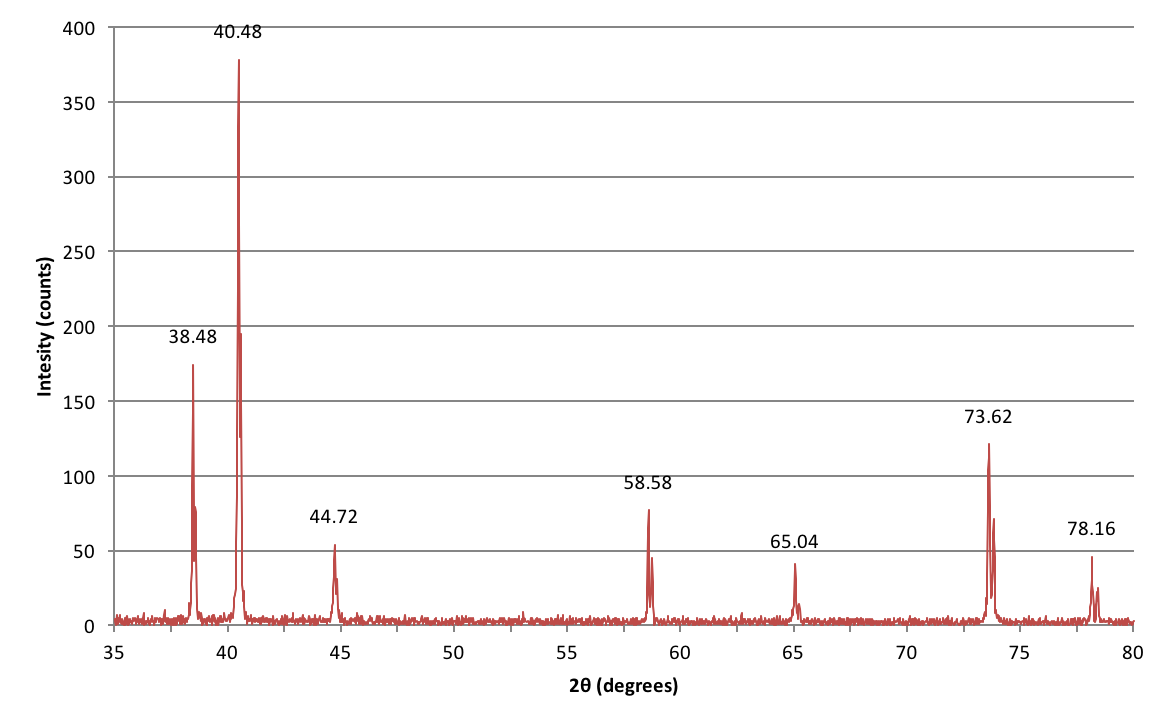
Come posso interpretare questi picchi?
| Struttura cristallina | Condizioni |
|---|---|
| Cubico semplice | tutti i valori h, k, l |
| Cubico centrato sul corpo | h+k+l devono essere pari |
| Cubico centrato sulla faccia | h, k, e l devono essere tutti dispari o tutti pari |
I fattori di struttura tengono conto dei casi in cui un piano può trovarsi a metà strada tra due piani vicini e causare un’interferenza distruttiva. Questi fattori risultano in una serie di regole per diverse geometrie di strutture cristalline che determinano quando l’interferenza costruttiva può verificarsi. La tabella sopra elenca i parametri dell’indice di Miller in cui si verifica l’interferenza costruttiva. Una tabella più estesa è mostrata qui sotto. Confrontando i rapporti di sin2θ (indicati come $Q^2$ nella seconda tabella) per diversi picchi di diffrazione, la struttura del cristallo e gli indici di Miller possono essere determinati.
| Piano cristallino (hkl) | $Q^2$ | Lattiche spaziali da cui sono possibili riflessioni | ||||
|---|---|---|---|---|---|---|
| 100 | 1 | SC | ||||
| 110 | 2 | SC | BCC | |||
| 111 | 3 | SC | FCC | DC | ||
| 200 | 4 | SC | BCC | FCC | ||
| 210 | 5 | SC | ||||
| 211 | 6 | SC | BCC | BCC | ||
| – | 7 | |||||
| 220 | 8 | SC | BCC | FCC | DC | |
| 300, 221 | 9 | SC | ||||
| 310 | 10 | SC | BCC | C | ||
| 311 | 11 | SC | FCC | DC | ||
| 222 | 12 | SC | BCC | FCC | ||
| 320 | 13 | SC | ||||
| 321 | 14 | SC | BCC | |||
| – | 15 | |||||
| 400 | 16 | SC | BCC | FCC | DC | |
X-La diffrazione dei raggi X ha una vasta gamma di applicazioni per la caratterizzazione dei materiali. Può essere usata come metodo sperimentale per determinare sperimentalmente il volume di una cella unitaria per i calcoli teorici della densità. Inoltre, se il materiale è sotto stress residuo, il reticolo distorto mostrerà una gamma di spaziature d che soddisfano la legge di Bragg, risultando in picchi di diffrazione molto più ampi. La larghezza del picco di diffrazione può anche essere usata per determinare la dimensione delle particelle.