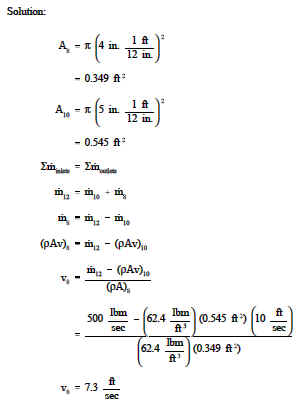Fluid Flow Table of Contents
Hydraulic and Pneumatic Knowledge
Fluid Power Equipment
Continuity Equation Fluids Flow
L’equazione di continuità è semplicemente una espressione matematica del principio di conservazione della massa. Per un volume di controllo che ha una sola entrata e una sola uscita, il principio di conservazione della massa afferma che, per un flusso stazionario, la portata di massa nel volume deve essere uguale alla portata di massa in uscita. L’equazione di continuità per questa situazione è espressa dall’equazione 3-5.

Per un volume di controllo con entrate e uscite multiple, il principio di conservazione della massa richiede che la somma delle portate di massa nel volume di controllo sia uguale alla somma delle portate di massa in uscita dal volume di controllo. L’equazione di continuità per questa situazione più generale è espressa dall’equazione 3-6.
![]()
Una delle applicazioni più semplici dell’equazione di continuità è la determinazione della variazione della velocità del fluido dovuta all’espansione o alla contrazione del diametro di un tubo.
Esempio: Equazione di continuità – Espansione delle tubazioni
Il flusso allo stato stazionario esiste in un tubo che subisce un’espansione graduale da un diametro di 6 pollici a un diametro di 8 pollici. La densità del fluido nel tubo è costante a 60,8 lbm/ft3. Se la velocità del flusso è 22.4 ft/sec nella sezione di 6 pollici, qual è la velocità del flusso nella sezione di 8 pollici?
Soluzione:
Dall’equazione di continuità sappiamo che la portata in massa nella sezione di 6 pollici deve essere uguale alla portata in massa nella sezione di 8 pollici. Lasciando che il pedice 1 rappresenti la sezione da 6 pollici e il 2 rappresenti la sezione da 8 pollici, abbiamo quanto segue.
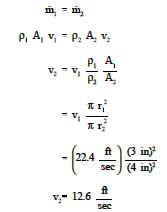
Quindi, usando l’equazione di continuità, troviamo che l’aumento del diametro del tubo da 6 a 8 pollici ha causato una diminuzione della velocità di flusso da 22.4 a 12.6 ft/sec.
L’equazione di continuità può anche essere usata per mostrare che una diminuzione del diametro del tubo causerà un aumento della velocità del flusso.
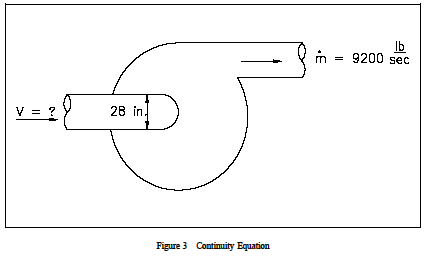
Esempio: Equazione di continuità – Pompa centrifuga Il diametro di ingresso della pompa di raffreddamento del reattore mostrato nella Figura 3 è di 28 pollici, mentre il flusso in uscita attraverso la pompa è di 9200 lbm/sec. La densità dell’acqua è di 49 lbm/ft3. Qual è la velocità all’ingresso della pompa?

L’esempio precedente indica che la portata in entrata nel sistema è uguale a quella in uscita dal sistema. Lo stesso concetto è vero anche se più di un percorso di flusso può entrare o uscire dal sistema allo stesso tempo. Il bilancio di massa è semplicemente regolato per affermare che la somma di tutti i flussi che entrano nel sistema è uguale alla somma di tutti i flussi che escono dal sistema se esistono condizioni di stato stazionario. Un esempio di questo caso fisico è incluso nel seguente esempio.
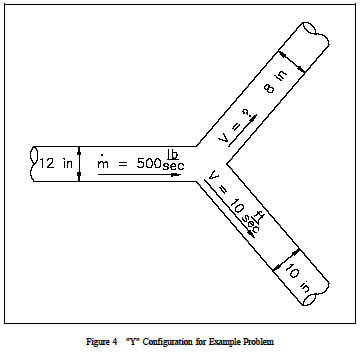
Esempio: Equazione di continuità – uscite multiple
Un sistema di tubazioni ha una configurazione a “Y” per separare il flusso come mostrato nella figura 4. Il diametro del tratto di ingresso è di 12 pollici, e i diametri dei tratti di uscita sono di 8 e 10 pollici. La velocità nella gamba da 10 pollici è di 10 piedi/sec. Il flusso attraverso la parte principale è di 500 lbm/sec. La densità dell’acqua è 62,4 lbm/ft3. Qual è la velocità in uscita dal tratto di tubo da 8 pollici?