- La connettività è un concetto base della teoria dei grafi. Definisce se un grafico è connesso o disconnesso. Senza connettività, non è possibile attraversare un grafico da un vertice ad un altro vertice.
- Un grafico si dice connesso se esiste un percorso tra ogni coppia di vertici. Da ogni vertice a qualsiasi altro vertice ci deve essere un percorso da attraversare. Questo è chiamato la connettività di un grafico.
- Un grafico si dice disconnesso, se esistono più vertici e bordi disconnessi.
- Le teorie della connettività dei grafi sono essenziali nelle applicazioni di rete, nelle reti di trasporto di routing, nella tolleranza di rete ecc.
Esempio
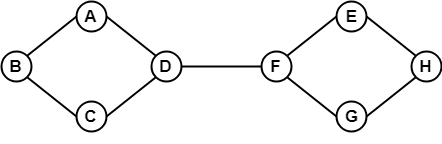
Nell’esempio precedente, è possibile viaggiare da un vertice ad un altro vertice. Qui, possiamo passare dal vertice B ad H usando il percorso B -> A -> D -> F -> E -> H. Quindi è un grafo connesso.
Esempio
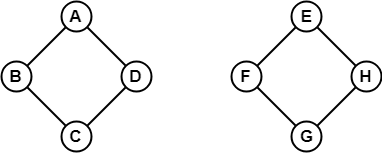
Nell’esempio precedente, non è possibile passare dal vertice B ad H perché non c’è nessun percorso tra loro direttamente o indirettamente. Quindi, è un grafo disconnesso.
Vediamo alcuni concetti di base della connettività.
Verice tagliato
Un singolo vertice la cui rimozione disconnette un grafo è chiamato un vertice tagliato.
Sia G un grafo connesso. Un vertice v di G è detto un vertice tagliato di G, se G-v (Rimuovere v da G) risulta un grafo disconnesso.
Quando rimuoviamo un vertice da un grafo allora il grafo si romperà in due o più grafi. Questo vertice è chiamato un vertice tagliato.
Nota: Sia G un grafico con n vertici:
- Un grafico connesso G può avere al massimo (n-2) vertici tagliati.
- Rimuovere un vertice tagliato può lasciare un grafico disconnesso.
- Rimuovere un vertice può aumentare il numero di componenti di un grafico di almeno uno.
- Ogni vertice non dipendente di un albero è un vertice tagliato.
Esempio 1

Esempio 2
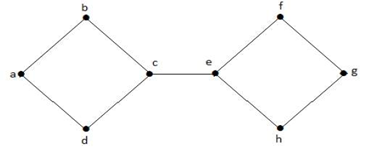
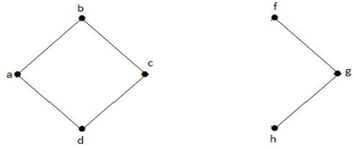
Nel grafico sopra, il vertice ‘e’ è un vertice tagliato. Dopo aver rimosso il vertice ‘e’ dal grafico di cui sopra, il grafico diventerà un grafico disconnesso.
Bordo tagliato (ponte)
Un bordo tagliato o ponte è un singolo bordo la cui rimozione disconnette un grafico.
Lasciamo che G sia un grafico connesso. Un bordo e di G è detto un bordo tagliato di G, se G-e (Rimuovere e da G) risulta un grafo disconnesso.
Quando rimuoviamo un bordo da un grafo allora il grafo si romperà in due o più grafi. Questo bordo rimosso è chiamato bordo tagliato o ponte.
Nota: Sia G un grafico con n vertici:
- Un grafico connesso G può avere al massimo (n-1) bordi tagliati.
- Rimuovere un bordo tagliato può lasciare un grafico disconnesso.
- La rimozione di un bordo può aumentare il numero di componenti di un grafo al massimo di uno.
- Un bordo tagliato ‘e’ non deve essere parte di nessun ciclo in G.
- Se esiste un bordo tagliato, allora deve esistere anche un vertice tagliato perché almeno un vertice di un bordo tagliato è un vertice tagliato.
- Se esiste un vertice tagliato, allora l’esistenza di qualsiasi bordo tagliato non è necessaria.
Esempio 1
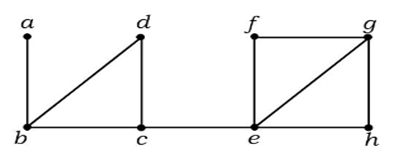
Nel grafico sopra, il bordo (c, e) è un bordo tagliato. Dopo aver rimosso questo bordo dal suddetto grafico, il grafico diventerà un grafico disconnesso.
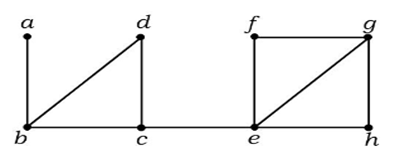
Esempio 2
Nel grafico sopra, il bordo (c, e) è un cut-edge. Dopo aver rimosso questo bordo dal grafico di cui sopra, il grafico diventerà un grafico disconnesso.
Insieme di taglio
In un grafico connesso G, un insieme di taglio è un insieme S di bordi con le seguenti proprietà:
- La rimozione di tutti i bordi in S disconnette G.
- La rimozione di alcuni dei bordi (ma non tutti) in S non disconnette G.
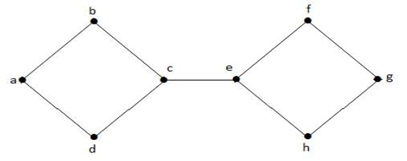
Esempio 1
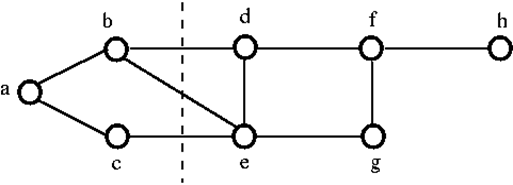
Per disconnettere il grafico G di cui sopra, dobbiamo rimuovere i tre bordi, cioè bd, be e ce. Non possiamo disconnetterlo rimuovendo solo due dei tre bordi. Quindi, {bd, be, ce} è un insieme tagliato.
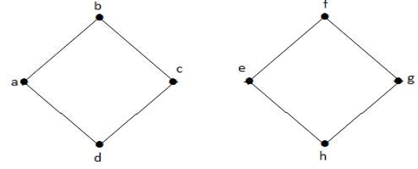
Dopo aver rimosso l’insieme tagliato dal grafico di cui sopra, sarebbe come segue:
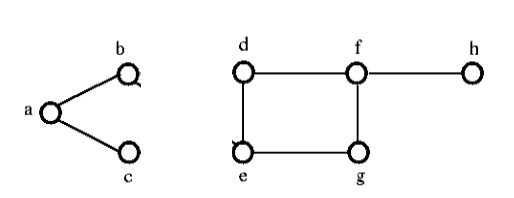
Connettività dei bordi
La connettività dei bordi di un grafico connesso G è il numero minimo di bordi la cui rimozione rende G disconnesso. Viene indicato con λ(G).
Quando λ(G) ≥ k, allora il grafico G si dice k-edge-connected.
Esempio
Vediamo un esempio,
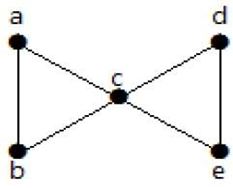
Dal grafico precedente, rimuovendo due bordi minimi, il grafico connesso diventa un grafico disconnesso. Quindi, la sua connettività dei bordi è 2. Quindi il grafico di cui sopra è un grafico connesso con 2 bordi.
Ecco i seguenti quattro modi per disconnettere il grafico rimuovendo due bordi:
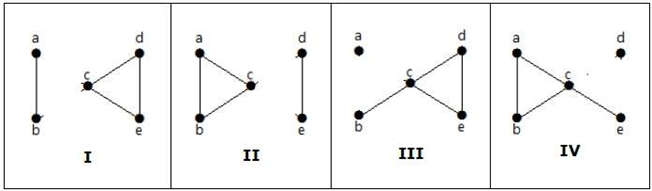
Connettività dei vertici
La connettività (o connettività dei vertici) di un grafico connesso G è il numero minimo di vertici la cui rimozione rende G disconnesso o riduce a un grafico banale. Viene indicato con K(G).
Il grafo si dice connesso a k o connesso a k vertici quando K(G) ≥ k. Per rimuovere un vertice dobbiamo rimuovere anche i bordi ad esso incidenti.
Esempio
Vediamo un esempio:
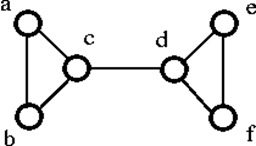
Il grafico G di cui sopra può essere disconnesso rimuovendo il singolo vertice ‘c’ o ‘d’. Quindi, la sua connettività dei vertici è 1. Pertanto, è un grafo connesso a 1.