Ogni volta che si discute della previsione dei modelli, è importante capire gli errori di previsione (bias e varianza). C’è un compromesso tra la capacità di un modello di minimizzare la distorsione e la varianza. Ottenere una corretta comprensione di questi errori ci aiuterebbe non solo a costruire modelli accurati ma anche ad evitare l’errore di overfitting e underfitting.
Partiamo quindi dalle basi e vediamo come fanno la differenza per i nostri modelli di apprendimento automatico.
Che cos’è il bias?
Il bias è la differenza tra la previsione media del nostro modello e il valore corretto che stiamo cercando di prevedere. Un modello con un alto bias presta poca attenzione ai dati di allenamento e semplifica eccessivamente il modello. Porta sempre ad un alto errore sui dati di allenamento e di test.
Che cos’è la varianza?
La varianza è la variabilità della previsione del modello per un dato punto di dati o un valore che ci dice la diffusione dei nostri dati. Un modello con un’alta varianza presta molta attenzione ai dati di allenamento e non generalizza sui dati che non ha mai visto prima. Di conseguenza, tali modelli si comportano molto bene sui dati di addestramento ma hanno alti tassi di errore sui dati di test.
Matematicamente
Lasciamo la variabile che stiamo cercando di prevedere come Y e le altre covariate come X. Assumiamo che ci sia una relazione tra i due tale che
Y=f(X) + e
dove e è il termine di errore ed è normalmente distribuito con una media di 0.
Faremo un modello f^(X) di f(X) usando la regressione lineare o qualsiasi altra tecnica di modellazione.
Quindi l’errore quadratico atteso in un punto x è
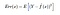
La Err(x) può essere ulteriormente scomposto come

Err(x) è la somma di Bias², la varianza e l’errore irriducibile.
L’errore irriducibile è l’errore che non può essere ridotto creando buoni modelli. È una misura della quantità di rumore nei nostri dati. Qui è importante capire che non importa quanto bene facciamo il nostro modello, i nostri dati avranno una certa quantità di rumore o errore irriducibile che non può essere rimosso.
Bias e varianza usando il diagramma dell’occhio di bue

Nel diagramma sopra, il centro dell’obiettivo è un modello che predice perfettamente i valori corretti. Man mano che ci allontaniamo dall’occhio di bue, le nostre previsioni diventano sempre peggiori. Possiamo ripetere il nostro processo di costruzione del modello per ottenere successi separati sul bersaglio.
Nell’apprendimento supervisionato, l’underfitting avviene quando un modello non è in grado di catturare il modello sottostante dei dati. Questi modelli di solito hanno un alto bias e una bassa varianza. Succede quando abbiamo una quantità molto ridotta di dati per costruire un modello accurato o quando cerchiamo di costruire un modello lineare con dati non lineari. Inoltre, questo tipo di modelli sono molto semplici per catturare i modelli complessi nei dati come la regressione lineare e logistica.
Nell’apprendimento supervisionato, l’overfitting avviene quando il nostro modello cattura il rumore insieme al modello sottostante nei dati. Succede quando addestriamo molto il nostro modello su serie di dati rumorosi. Questi modelli hanno un basso bias e un’alta varianza. Questi modelli sono molto complessi come gli alberi decisionali che sono inclini all’overfitting.

Perché il Bias Variance Tradeoff?
Se il nostro modello è troppo semplice e ha pochi parametri allora può avere un alto bias e bassa varianza. D’altra parte, se il nostro modello ha un gran numero di parametri, allora avrà un’alta varianza e un basso bias. Quindi abbiamo bisogno di trovare il giusto/buon equilibrio senza sovraadattare e sottoadattare i dati.
Questo compromesso nella complessità è il motivo per cui c’è un compromesso tra bias e varianza. Un algoritmo non può essere più complesso e meno complesso allo stesso tempo.
Errore totale
Per costruire un buon modello, dobbiamo trovare un buon equilibrio tra bias e varianza tale da minimizzare l’errore totale.


Un equilibrio ottimale di bias e varianza non sovraadatta né sottoadatta il modello.
Pertanto la comprensione di bias e varianza è fondamentale per capire il comportamento dei modelli di previsione.
Grazie per la lettura!