Learning Outcomes

  • Meghatározni, hogy az adatok vagy egy forgatókönyv lineáris vagy geometriai növekedést írnak-e le
  • Növekedési ütemek, kezdőértékek vagy pontértékek meghatározása szóban, grafikusan kifejezve, vagy numerikusan, és fordítsa le őket számításban használható formátumba
  • Kalkuláljon rekurzív és explicit egyenleteket lineáris és geometriai növekedésre elegendő információ birtokában, és használja ezeket az egyenleteket előrejelzések készítésére

A lineáris növekedés meghatározó jellemzője, hogy a változás mértéke állandó. Az állandó változáshoz tartozó koordinátapárok ábrázolása egyenes vonalat, a lineáris növekedés alakját eredményezi. Ebben a szakaszban formalizáljuk a lineáris növekedés leírásának módját matematikai kifejezések és fogalmak segítségével. A szakasz végére képesek leszünk a lineáris növekedésre vonatkozó rekurzív és explicit egyenleteket is felírni a kiindulási feltételek vagy a változás állandósága mellett. Képes leszel továbbá felismerni a lineáris és a geometriai növekedés közötti különbséget egy grafikon vagy egy egyenlet alapján.

Lineáris (algebrai) növekedés

Növekedés előrejelzése

Marco antik szódásüvegek gyűjtője. Gyűjteménye jelenleg 437 palackot tartalmaz. Minden évben annyi pénzt tervez be a költségvetésébe, hogy 32 új palackot tud vásárolni. Meg tudjuk-e határozni, hogy 5 év múlva hány palackja lesz, és mennyi időbe telik, amíg a gyűjteménye eléri az 1000 palackot?

Noha valószínűleg mindkét kérdést meg tudnánk oldani egyenlet vagy formális matematika nélkül, formalizáljuk a probléma megközelítését, hogy bonyolultabb kérdések megválaszolására is módot adjunk.

Tegyük fel, hogy Pn az üvegek számát vagy populációját jelenti, amellyel Marco n év után rendelkezik. Tehát P0 jelentené a mostani palackok számát, P1 jelentené a palackok számát 1 év múlva, P2 jelentené a palackok számát 2 év múlva, és így tovább. Azt, hogy hogyan változik Marco palackgyűjteménye, a következőkkel írhatjuk le:

P0 = 437

Pn = Pn-1 + 32

Ezt rekurzív összefüggésnek nevezzük. A rekurzív kapcsolat olyan képlet, amely egy sorozat következő értékét az előző értékekhez kapcsolja. Itt az n. év palackjainak számát úgy találjuk meg, hogy 32-t hozzáadunk az előző év palackjainak számához, Pn-1-hez. Ezt az összefüggést felhasználva kiszámíthatjuk:

P1 = P0 + 32 = 437 + 32 = 469

P2 = P1 + 32 = 469 + 32 = 501

P3 = P2 + 32 = 501 + 32 = 533

P4 = P3 + 32 = 533 + 32 = 565

P5 = P4 + 32 = 565 + 32 = 597

Válaszoltunk arra a kérdésre, hogy Marco hány palackja lesz 5 év múlva.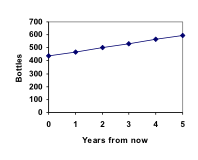

Az azonban, hogy megoldjuk, mennyi idő alatt éri el a gyűjteménye az 1000 palackot, sokkal több számítást igényelne.

Míg a rekurzív összefüggések kiválóan alkalmasak arra, hogy egyszerűen és tisztán leírjuk, hogyan változik egy mennyiség, nem alkalmasak előrejelzések készítésére vagy olyan problémák megoldására, amelyek messze a jövőbe nyúlnak. Ehhez az összefüggés zárt vagy explicit formája előnyösebb. Egy explicit egyenlet lehetővé teszi, hogy közvetlenül kiszámítsuk Pn-t, anélkül, hogy ismernünk kellene Pn-1-et. Bár az explicit egyenletet már kitalálhatjuk, vezessük le a rekurzív képletből. Ezt úgy tehetjük meg, hogy menet közben szelektíven nem egyszerűsítünk:

P1 = 437 + 32 = 437 + 1(32)

P2 = P1 + 32 = 437 + 32 + 32 = 437 + 2(32)

P3 = P2 + 32 = (437 + 2(32)) + 32 = 437 + 3(32)

P4 = P3 + 32 = (437 + 3(32)) + 32 = 437 + 4(32)

Valószínűleg most már látod a mintát, és általánosíthatod, hogy

Pn = 437 + n(32) = 437 + 32n

Az egyenletet felhasználva kiszámolhatjuk, hány palackja lesz 5 év után:

P5 = 437 + 32(5) = 437 + 160 = 597

Megoldhatjuk most azt is, hogy mikor éri el a gyűjtemény az 1000 palackot, ha Pn helyébe 1000-et teszünk, és megoldjuk n

1000 = 437 + 32n

563 = 32n

n = 563/32 = 17.59

Így Marco 18 év alatt eléri az 1000 palackot.

A képlet meghatározásának és a Marco palackgyűjteményére vonatkozó feladat megoldásának lépéseit a következő videókban részletesen elmagyarázzuk.

A példában Marco gyűjteménye minden évben ugyanannyi palackkal nőtt. Ez az állandó változás a lineáris növekedés meghatározó jellemzője. A Marco gyűjteményére kiszámított értékeket ábrázolva láthatjuk, hogy az értékek egy egyenes vonalat alkotnak, a lineáris növekedés alakját.

Lineáris növekedés

Ha egy mennyiség P0 méretről indul és minden időszakban d-vel növekszik, akkor az n időperiódus utáni mennyiséget az alábbi összefüggések valamelyikével határozhatjuk meg:

Rekurzív forma

Pn = Pn-1 + d

Explicit forma

Pn = P0 + d n

Ebben az egyenletben a d a közös különbséget jelenti – azt a mennyiséget, amelyet a populáció minden egyes alkalommal, amikor n 1-gyel nő.

Kapcsolódás az előzetes tanuláshoz: Meredekség és metszéspont

A közös különbséget, d-t, lineáris egyenletünkben meredekségként ismerheted fel. Valójában az egész explicit egyenletnek ismerősnek kell tűnnie – ez ugyanaz a lineáris egyenlet, amit algebrában tanultál, valószínűleg y = mx + b alakban.

A standard algebrai egyenletben y = mx + b, b volt az y-intercept, vagyis az y értéke, amikor x nulla. Az általunk használt egyenlet formájában P0-t használjuk ennek a kezdeti mennyiségnek a jelölésére.

Az y = mx + b egyenletben emlékezzünk arra, hogy m volt a meredekség. Erre úgy emlékezhetsz, mint “emelkedés a futáshoz”, vagy az y változása osztva az x változásával. Akárhogy is, ugyanazt a dolgot képviseli, mint az általunk használt közös különbség, d – azt az összeget, amennyivel a Pn kimenet változik, amikor az n bemenet 1-nel nő.

Az y = mx + b és a Pn = P0 + d n egyenletek ugyanazt jelentik, és ugyanúgy használhatók. Csak kicsit másképp írjuk le.

Példák

Egy nemzeti erdőben a szarvasállományt 2003-ban 12 000 egyedre, 2007-ben pedig ismét 15 000 egyedre mértük. Ha a populáció továbbra is lineárisan növekszik ezzel az ütemmel, mennyi lesz a szarvasállomány 2014-ben?

Megoldás megjelenítése

Kezdésnek meg kell határoznunk, hogyan fogjuk mérni az n-t. Ne feledjük, hogy P0 a populáció, amikor n = 0, tehát valószínűleg nem akarjuk szó szerint a 0 évet használni. Mivel már ismerjük a 2003-as népességet, határozzuk meg, hogy n = 0 a 2003-as év.

Ezután P0 = 12 000.

A következőkben meg kell találnunk d-t. Ne feledjük, hogy d az időszakonkénti növekedés, ebben az esetben az évenkénti növekedés. A két mérés között a népesség 15 000-12 000 = 3 000 fővel nőtt, de ennyi növekedéshez 2007-2003 = 4 év kellett. Az egy évre jutó növekedést úgy találjuk meg, hogy elosztjuk: 3000 szarvas / 4 év = 750 szarvas 1 év alatt.

Alternatívaként használhatjuk az algebrából ismert meredekségi képletet a közös különbség meghatározásához, megjegyezve, hogy a populáció a képlet kimenete, az idő pedig a bemenet.

d= meredekség=\frac{\text{changeinoutput}}{\text{changeininput}}=\frac{15,000-12,000}{2007-2003}=\frac{3000}{4}=750

Egyenletünket most már leírhatjuk, bármelyik formában is szeretnénk.

Rekurzív forma

P0 = 12,000

Pn = Pn-1 + 750

Explicit forma

Pn = 12,000 + 750(n)

A kérdés megválaszolásához először is meg kell jegyeznünk, hogy a 2014-es év n = 11 lesz, mivel 2014 11 évvel 2003 után van. Ehhez a számításhoz könnyebb lesz az explicit formát használni:

P11 = 12 000 + 750(11) = 20 250 elk

Tekintse meg a példát itt.

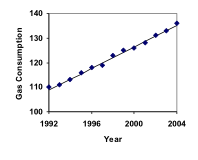
A benzinfogyasztás az USA-ban folyamatosan növekszik. Az alábbiakban az 1992 és 2004 közötti fogyasztási adatokat mutatjuk be. Keressen egy modellt ezekre az adatokra, és használja azt a 2016-os fogyasztás előrejelzésére. Ha a tendencia folytatódik, mikor éri el a fogyasztás a 200 milliárd gallont?

.

év ’92 ’93 ’94 ’95 ’96 ’97 ’98 ’99 ’00 ’01 ’02 ’03 ’04
Fogyasztás (milliárd Ft. gallon) 110 111 113 116 118 119 123 125 126 128 131 133 136
Megoldás megjelenítése

Az adatok ábrázolása, úgy tűnik, hogy megközelítőleg lineáris kapcsolat áll fenn:

Míg vannak fejlettebb statisztikai technikák, amelyekkel egy egyenletet találhatunk az adatok modellezésére, ahhoz, hogy képet kapjunk arról, hogy mi történik, az adatok két darabjának – talán az 1993-as és a 2003-as adatok – felhasználásával találhatunk egy egyenletet.

Ha n = 0 megfelelne 1993-nak, akkor P0 = 111 milliárd gallon lenne.

Ahhoz, hogy megtaláljuk d-t, tudnunk kell, hogy évente átlagosan mennyivel nőtt a gázfogyasztás. 1993 és 2003 között a gázfogyasztás 111 milliárd gallonról 133 milliárd gallonra nőtt, ami 10 év alatt összesen 133 – 111 = 22 milliárd gallon változást jelent. Ez 22 milliárd gallon / 10 év = 2,2 milliárd gallon átlagos változást ad évente.

Egyenlítően,

d=slope=\frac{\text{changeinoutput}}{\text{changeinput}}=\frac{133-111}{10-0}=\frac{22}{10}=2.2milliárd gallon évente

Egyenletünket most már felírhatjuk bármelyik formában, amelyiket preferáljuk.

Rekurzív forma

P0 = 111

Pn = Pn-1 + 2.2

Explicit forma

Pn = 111 + 2.2n

Az explicit forma segítségével kiszámított értékek és az eredeti adatokkal való ábrázolása megmutatja, hogy modellünk mennyire jól illeszkedik az adatokhoz.

Modellünk segítségével most előrejelzéseket tehetünk a jövőre vonatkozóan, feltételezve, hogy a korábbi trend változatlanul folytatódik. A 2016-os benzinfogyasztás előrejelzéséhez:

n = 23 (2016 – 1993 = 23 évvel később)

P23 = 111 + 2,2(23) = 161,6

Modellünk azt jósolja, hogy az USA 161.6 milliárd gallon benzint 2016-ban, ha a jelenlegi tendencia folytatódik.

Hogy megtaláljuk, mikor éri el a fogyasztás a 200 milliárd gallont, Pn = 200, és megoldjuk n-re:

Pn = 200 Helyettesítsük Pn-t a modellünkkel

111 + 2.2n = 200 Vonjuk ki mindkét oldalból a 111-et

2,2n = 89 Osszuk el mindkét oldalt 2,2-vel

n = 40,4545

Ez azt mondja, hogy a fogyasztás körülbelül 40 évvel 1993 után, azaz 2033-ban fogja elérni a 200 milliárdot.

A válasz elérésének lépéseit a következő videó részletezi.

Az n hónapos edzőtermi tagság dollárban kifejezett költségét a Pn = 70 + 30n explicit egyenlet segítségével írhatjuk le. Mit mond ez az egyenlet?

Megoldás megjelenítése

A P0 értéke ebben az egyenletben 70, tehát a kezdeti induló költség 70 dollár. Ez azt mondja nekünk, hogy az edzőterembe való belépésnek 70 $-os kezdeti vagy induló díjnak kell lennie.

A d értéke az egyenletben 30, tehát a költség minden hónapban 30 $-ral nő. Ez azt mondja nekünk, hogy az edzőterem havi tagsági díja 30 dollár havonta.

A példa magyarázatát az alábbiakban részletezzük.

Kipróbálni

A háztartásbeli apák száma Kanadában folyamatosan nő. Bár a tendencia nem tökéletesen lineáris, de meglehetősen lineáris. Az 1976-os és 2010-es adatok alapján keressen egy explicit képletet az otthonmaradó apák számára, majd használja azt arra, hogy megjósolja a 2020-as számot.

év 1976 1984 1991 2000 2010
# of Stay -at-at-otthoni apák 20610 28725 43530 47665 53555
Show Solution

Hagyjuk, hogy n= 0 megfeleljen 1976-nak, akkor P_0= 20 610.
1976-tól 2010-ig az otthonmaradó apák száma 53 555 – 20 610 = 32 945-tel nőtt
Ez 34 év alatt történt, ami 32 945 / 34 = 969 közös különböző d-t ad.
P_n= 20,610 + 969n
A 2020-ra vonatkozó előrejelzésben n = 44, P(44) = 20,610 + 969(44) = 63,246 otthonmaradó apát használunk 2020-ban.

Mikor a jó modellek rosszra fordulnak

Mikor matematikai modelleket használunk jövőbeli viselkedés előrejelzésére, fontos szem előtt tartani, hogy nagyon kevés trend fog a végtelenségig folytatódni.

Példa

Tegyük fel, hogy egy négyéves fiú jelenleg 39 hüvelyk magas, és azt mondják, hogy évente 2,5 hüvelyk növekedést várunk tőle.

Felállíthatunk egy növekedési modellt, ahol n = 0 megfelel a 4 évesnek.

Rekurzív forma

P0 = 39

Pn = Pn-1 + 2,5

Explicit forma

Pn = 39 + 2.5(n)

Így 6 éves korában várhatóan

P2 = 39 + 2,5(2) = 44 hüvelyk magas lesz

Minden matematikai modell előbb-utóbb összeomlik. Természetesen nem várhatjuk el, hogy ez a fiú egész életében ugyanolyan ütemben növekedjen. Ha így lenne, 50 éves korában

P46 = 39 + 2,5(46) = 154 hüvelyk magas lenne = 12,8 láb magas!

Amikor bármilyen matematikai modellt használunk, meg kell fontolnunk, hogy milyen bemeneti adatokat ésszerű használni. Amikor extrapolálunk, vagy előrejelzéseket teszünk a jövőre, feltételezzük, hogy a modell továbbra is érvényes marad.

Nézze meg a lineáris növekedési modell e bontásának videós magyarázatát itt.

Exponenciális (geometriai ) növekedés

Népességnövekedés

Tegyük fel, hogy egy tóban minden évben a halaknak csak 10%-ának van túlélő utóda. Ha tavaly 100 hal volt a tóban, akkor most 110 hal lenne. Ha tavaly 1000 hal volt a tóban, akkor most 1100 hal lenne. Minden gátló tényező hiányában az emberek és állatok populációi hajlamosak arra, hogy minden évben a meglévő populáció egy százalékával növekedjenek.


Tegyük fel, hogy tavunk 1000 hallal indult, és a halak 10%-ának minden évben vannak túlélő utódai. Mivel 1000 hallal kezdtünk, P0 = 1000. Hogyan számoljuk ki P1-et? Az új populáció a régi populáció lesz, plusz további 10%. Szimbolikusan:

P1 = P0 + 0,10P0

Megjegyezzük, hogy ez faktorálással rövidebb formába sűríthető:

P1 = P0 + 0,10P0 = 1P0 + 0,10P0 = (1+ 0,10)P0 = 1,10P0

Míg 10% a növekedés mértéke, addig 1,10 a növekedés szorzója. Vegyük észre, hogy az 1,10 úgy képzelhető el, mint “az eredeti 100% plusz további 10%.”

Halállományunk esetében

P1 = 1,10(1000) = 1100

A későbbi években kiszámíthatjuk a populációt:

P2 = 1,10P1 = 1,10(1100) = 1210

P3 = 1,10P2 = 1,10(1210) = 1331

Megjegyezzük, hogy az első évben az állomány 100 hallal, a második évben 110 hallal, a harmadik évben pedig 121 hallal nőtt.

Míg a százalékos növekedés állandó, a halak számának tényleges növekedése minden évben növekszik.

Ezeket az értékeket grafikonon ábrázolva láthatjuk, hogy ez a növekedés nem egészen lineárisnak tűnik.

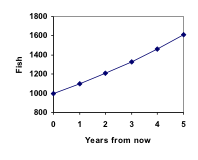
A halakra vonatkozó forgatókönyv végigjárása itt tekinthető meg:

Hogy jobban lássuk, hogyan hat ez a százalékos növekedés a dolgokra, szükségünk van egy explicit formára, hogy gyorsan kiszámíthassuk a távolabbi jövőbeni értékeket.

Mint a lineáris modellnél is tettük, a rekurzív egyenletből fogunk kiindulni:

P1 = 1,10(P0 )= 1,10(1000)

P2 = 1,10(P1 )= 1,10(1,10(1000)) = 1,102(1000)

P3 = 1.10(P2 )= 1,10(1,102(1000)) = 1,103(1000)

P4 = 1,10(P3 )= 1,10(1,103(1000)) = 1,104(1000)

A mintát megfigyelve általánosíthatjuk az explicit formát:

Pn = 1.10n(1000), vagy egyenértékűen: Pn = 1000(1.10n)

Ez alapján gyorsan kiszámíthatjuk a halak számát 10, 20 vagy 30 év alatt:

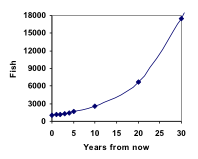
P10 = 1.1010(1000) = 2594

P20 = 1.1020(1000) = 6727

P30 = 1.1030(1000) = 17449

Ha ezeket az értékeket hozzáadjuk a grafikonunkhoz, egy olyan alakzatot kapunk, amely határozottan nem lineáris. Ha a halpopulációnk lineárisan, évente 100 hallal növekedett volna, akkor a populáció 30 év alatt csak 4000 halat ért volna el, míg ezzel a százalékos alapú, exponenciális növekedésnek nevezett növekedéssel csaknem 18000-et.

Egy videó, amely ennek a haltörténetnek az explicit modelljét mutatja be, itt tekinthető meg:

Az exponenciális növekedés során a populáció a populáció méretével arányosan növekszik, tehát ahogy a populáció egyre nagyobb lesz, ugyanaz a százalékos növekedés nagyobb számszerű növekedést fog eredményezni.

Exponenciális növekedés

Ha egy mennyiség P0 méretről indul, és minden időszakban R%-kal (tizedesjegyként r-rel írva) növekszik, akkor n időszak után a mennyiséget az alábbi összefüggések valamelyikével határozhatjuk meg:

Rekurzív forma

Pn = (1+r) Pn-1

Explicit forma

Pn = (1+r)n P0 vagy egyenértékűen: Pn = P0 (1+r)n

R növekedési rátának nevezzük.

Az (1+r) kifejezést nevezzük növekedési szorzónak, vagy közös arányszámnak.

Példa

2007 és 2008 között a WA állambeli Olympia lakossága közel 3%-kal 245 ezer főre nőtt. Ha ez a növekedési ütem folytatódna, mennyi lenne Olympia lakossága 2014-ben?

Megoldás megjelenítése

Amint korábban is tettük, először meg kell határoznunk, hogy melyik év felel meg n = 0-nak. Mivel ismerjük a 2008-as népességet, ésszerű lenne, ha 2008 megfelelne n = 0-nak, tehát P0 = 245 ezer. A 2014-es év ezután n = 6 lenne.

Tudjuk, hogy a növekedési ráta 3%, így r = 0,03.

Az explicit formát használva:

P6 = (1+0,03)6 (245 000) = 1,19405(245 000) = 292 542,25

A modell azt jósolja, hogy 2014-ben Olympia lakossága körülbelül 293 ezer fő lesz.

A következő videó részletesen elmagyarázza ezt a példát.

Exponensek kiértékelése számológéppel

Az olyan kifejezések kiértékeléséhez, mint (1,03)6, egyszerűbb lesz számológépet használni, mint 1,03-at hatszor megszorozni önmagával. A legtöbb tudományos számológépen van egy gomb az exponensek kiszámítására. Ez általában vagy így van feliratozva:

^ , yx , vagy xy .

Az 1,036 kiértékeléséhez beírnánk az 1,03 ^ 6, vagy 1,03 yx 6 értéket. Próbáld ki – körülbelül 1,1940523 körüli választ kell kapnod.

Kipróbáld

India a világ második legnépesebb országa, lakossága 2008-ban körülbelül 1,14 milliárd fő volt. A népesség évente körülbelül 1,34%-kal növekszik. Ha ez a tendencia folytatódik, mekkorára fog nőni India népessége 2020-ra?

Megoldás megjelenítése

A 2008-as évnek megfelelő n = 0-t használva, P_12= (1+0,0134)12(1,14) = körülbelül 1.337 milliárd ember 2020-ban

Példák

Egy barátom a Pn = 4600(1,072)n egyenletet használja, hogy megjósolja az éves tandíjat egy helyi főiskolán. Azt mondja, hogy a képlet a 2010 utáni évekre vonatkozik. Mit mond ez az egyenlet?

Megoldás megjelenítése

Az egyenletben P0 = 4600, ami a tandíj kezdőértéke, amikor n = 0. Ez azt mondja, hogy a tandíj 2010-ben 4600 dollár volt.

A növekedési szorzó 1,072, tehát a növekedés mértéke 0,072, azaz 7,2%. Ez azt mondja nekünk, hogy a tandíj várhatóan minden évben 7,2%-kal fog növekedni.

Azt mondhatjuk, hogy a tandíj 2010-ben 4600 dollár volt, és várhatóan minden évben 7,2%-kal fog növekedni.

Nézze meg a következőket, hogy ezt a példát kidolgozva lássa.

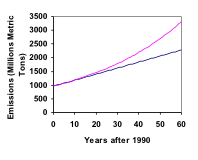
1990-ben a lakossági energiafelhasználás az USA-ban 962 millió tonna szén-dioxid kibocsátásért volt felelős. Ez a szám 2000-re 1182 millió metrikus tonnára emelkedett. Ha a kibocsátás exponenciálisan növekszik, és ugyanilyen ütemben folytatódik, akkor 2050-re mennyi lesz a kibocsátás?

Megoldás megjelenítése

A korábbiakhoz hasonlóan n = 0-nak fogjuk megfeleltetni 1990-et, mivel ez az év az első adatunk. Így P0 = 962 (millió tonna CO2) lesz. Ebben a feladatban nem a növekedési ütemet kapjuk meg, hanem azt, hogy P10 = 1182.

Ha n = 10, akkor az explicit egyenlet így néz ki:

P10 = (1+r)10 P0

A P0 értékét ismerjük, így azt beírhatjuk az egyenletbe:

P10 = (1+r)10 962

Azt is tudjuk, hogy P10 = 1182, így ezt behelyettesítve megkapjuk

1182 = (1+r)10 962

Ezt az egyenletet most megoldhatjuk a növekedési ütemre, r-re. Kezdjük azzal, hogy elosztjuk 962-vel.

\frac{1182}{962}={{(1+r)}^{10}}} Vegyük mindkét oldal 10. gyökét

\sqrt{\frac{1182}{962}}=1+r Vonjuk ki mindkét oldalból az 1-et

r=\sqrt{\frac{1182}{962}}-1=0,0208 = 2,08%

Ha tehát a kibocsátás exponenciálisan nő, akkor évente körülbelül 2,08%-kal nő. Most megjósolhatjuk a 2050-es kibocsátást, ha megtaláljuk a P60

P60 = (1+0,0208)60 962 = 3308,4 millió tonna CO2-t 2050-ben

Nézzen meg többet erről a példáról itt.

Kerekítés

A kerekítéssel kapcsolatban megjegyezzük, hogy ha a növekedési rátát 2,1%-ra kerekítettük volna, akkor a 2050-es kibocsátásra vonatkozó számításunk 3347 tonna lett volna. A 2%-ra kerekítés 3156-ra változtatta volna az eredményt. A növekedési ütemek közötti nagyon kis különbség exponenciális növekedés esetén nagymértékben felnagyítódik. Ezért ajánlott a növekedési ütemet a lehető legkisebb mértékben kerekíteni.

Ha kerekíteni kell, legalább három szignifikáns számjegyet – a vezető nullák utáni számokat – tartsunk meg. Így a 0,4162 ésszerűen kerekíthető 0,416-ra. Egy 0,001027-es növekedési ütemet ésszerűen kerekíthetünk 0,00103-ra.

Gyök kiértékelése a számológépen

Az előző példában egy szám 10. gyökét kellett kiszámítanunk. Ez más, mint az alapvető négyzetgyök, √ kivétele. Sok tudományos számológépen van egy gomb az általános gyökökhöz. Ez általában így van feliratozva:

\sqrt{x}

A 8 3. gyökének kiértékeléséhez például vagy beírjuk a 3 \sqrt{{{}} 8, vagy 8 \sqrt{{{}} 3, a számológéptől függően. Próbálja ki a sajátján, hogy lássa, melyiket használja – a válasznak 2 kell lennie.

Ha a számológépén nincs általános gyök gomb, akkor sincs minden veszve. Ehelyett használhatod az exponensek tulajdonságát, amely kimondja, hogy:

\sqrt{a}={a}^{\frac{1}{2}}}.

A 8 3. gyökének kiszámításához tehát használhatod a számológéped exponensgombját a 81/3 kiértékelésére. Ehhez írja be:

8 yx ( 1 ÷ 3 )

A zárójelek azt mondják a számológépnek, hogy az exponens elvégzése előtt ossza el az 1/3-at.

Kipróbálja

A közösségi oldal felhasználóinak száma februárban, a hivatalos megjelenéskor 45 ezer volt, és októberre 60 ezerre nőtt. Ha az oldal exponenciálisan növekszik, és a növekedés ugyanilyen ütemben folytatódik, hány felhasználóra számíthatnak két évvel a tőzsdére lépés után?

Megoldás megjelenítése

Itt az n-t nem években, hanem hónapokban fogjuk mérni, n = 0 megfelel annak a februárnak, amikor tőzsdére léptek. Így P_0= 45 ezer lesz. Október 8 hónappal később van, tehát P_8= 60.
P_8=(1+r)^{8}P_0
60=(1+r)^{8}45
\frac{60}{45}=(1+r)^8
\sqrt{\frac{60}{45}}=1+r
r=\sqrt{\frac{60}{45}}-1=0.0366\text{ vagy }3.66%
Az általános explicit egyenlet P_n =(1.0366)^{n}45. Ha 24 hónappal a tőzsdére lépésük után jósolunk, akkor P_{24}=(1.0366)^{24}45=106,63 ezer felhasználó.

Példa

Az utolsó példára visszatérve, az összehasonlítás kedvéért, mennyi lenne a szén-dioxid-kibocsátás 2050-ben, ha a kibocsátás lineárisan ugyanilyen ütemben nőne?

Megoldás megjelenítése

Újra azt kapjuk, hogy n = 0 megfelel 1990-nek, így P0 = 962. A d megtalálásához ugyanazt a megközelítést alkalmazhatjuk, mint korábban, megjegyezve, hogy a kibocsátás 10 év alatt 220 millió tonnával nőtt, ami évi 22 millió tonnás közös különbséget ad.

Alternatívaként használhatunk egy hasonló megközelítést, mint amit az exponenciális egyenlet megtalálásához használtunk. Ha n = 10, akkor az explicit lineáris egyenlet így néz ki:

P10 = P0 + 10d

A P0 értékét ismerjük, így azt beírhatjuk az egyenletbe:

P10 = 962 + 10d

Mivel tudjuk, hogy P10 = 1182, ezt behelyettesítve megkapjuk

1182 = 962 + 10d

Ezt az egyenletet most megoldhatjuk a közös különbségre, d-re.

1182 – 962 = 10d

220 = 10d

d = 22

Ez azt mondja, hogy ha a kibocsátás lineárisan változik, akkor évente 22 millió tonnával nő. A 2050-es kibocsátást megjósolva,

P60 = 962 + 22(60) = 2282 millió metrikus tonna.

Láthatjuk, hogy ez a szám lényegesen kisebb, mint az exponenciális növekedési modell előrejelzése. Több érték kiszámítása és ábrázolása segít szemléltetni a különbségeket.

Ez a példa bemutatása az alábbi videón látható.

Honnan tudjuk tehát, hogy melyik növekedési modellt használjuk, amikor adatokkal dolgozunk? Két megközelítés létezik, amelyeket lehetőség szerint együtt kell használni:

  1. Kettőnél több adatot keressünk. Ábrázoljuk az értékeket, és keressünk tendenciát. Úgy tűnik, hogy az adatok vonalszerűen változnak, vagy úgy tűnik, hogy az értékek felfelé görbülnek?
  2. Figyeljünk az adatokhoz hozzájáruló tényezőkre. Olyan dolgok, amelyekről azt várná, hogy lineárisan vagy exponenciálisan változnak? Például a szén-dioxid-kibocsátás esetében azt várhatnánk, hogy más tényezők hiányában szorosan kötődnek a népességi értékekhez, amelyek általában exponenciálisan változnak.

By: adminPosted on

Vélemény, hozzászólás?

Az e-mail-címet nem tesszük közzé.