Introduction
En informatique, un graphe acyclique dirigé (GAD) est un graphe dirigé sans cycles. Dans ce tutoriel, nous allons montrer comment faire un tri topologique sur un DAG en temps linéaire.
Tri topologique
Dans de nombreuses applications, nous utilisons des graphes acycliques dirigés pour indiquer les précédences entre les événements. Par exemple, dans un problème d’ordonnancement, il y a un ensemble de tâches et un ensemble de contraintes spécifiant l’ordre de ces tâches. Nous pouvons construire un DAG pour représenter les tâches. Les arêtes dirigées du DAG représentent l’ordre des tâches.
Envisageons un problème sur la façon dont une personne pourrait s’habiller pour une occasion formelle. Nous devons mettre plusieurs vêtements, tels que des chaussettes, un pantalon, des chaussures, etc. Certains vêtements doivent être enfilés avant les autres. Par exemple, nous devons mettre les chaussettes avant les chaussures. Certains vêtements peuvent être enfilés dans n’importe quel ordre, par exemple, les chaussettes et le pantalon. Nous pouvons utiliser un DAG pour illustrer ce problème:
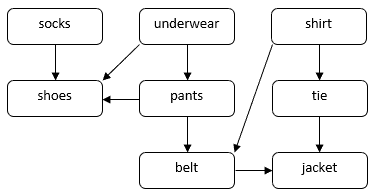
Dans ce DAG, les sommets correspondent aux vêtements. Une arête directe 
dans le DAG indique que nous devons mettre le vêtement 
avant le vêtement 
. Notre tâche consiste à trouver un ordre pour enfiler tous les vêtements tout en respectant les contraintes de dépendance. Par exemple, nous pouvons mettre les vêtements dans l’ordre suivant :
Un tri topologique d’un DAG 
est un ordre linéaire de tous ses sommets tel que si contient une arête , alors apparaît avant dans l’ordre. Pour un DAG, on peut construire un tri topologique dont le temps d’exécution est linéaire au nombre de sommets plus le nombre d’arêtes, soit 
.
Algorithme de Kahn
Dans un DAG, tout chemin entre deux sommets a une longueur finie car le graphe ne contient pas de cycle. Soit 
le plus long chemin de (sommet source) à (sommet destination). Puisque est le chemin le plus long, il ne peut y avoir d’arête entrante vers . Par conséquent, un DAG contient au moins un sommet qui n’a pas d’arête entrante.
3.1. Algorithme de Kahn
Dans l’algorithme de Kahn, on construit un tri topologique sur un DAG en trouvant les sommets qui n’ont pas d’arêtes entrantes :
Dans cet algorithme, on calcule d’abord les valeurs d’in-degré pour tous les sommets.
Puis, on commence par un sommet dont l’in-degré est 0 et on le met à la fin de la liste de sortie. Une fois que nous choisissons un sommet, nous mettons à jour les valeurs d’in-degré de ses sommets adjacents car le sommet et ses arêtes de sortie sont retirés du graphe.
Nous pouvons répéter le processus ci-dessus jusqu’à ce que nous choisissions tous les sommets. La liste de sortie est alors un tri topologique du graphe.
3.2. Complexité temporelle
Pour calculer les in-degrés de tous les sommets, nous devons visiter tous les sommets et arêtes de . Par conséquent, le temps d’exécution est pour les calculs de in-degrees. Pour éviter de recalculer ces valeurs, nous pouvons utiliser un tableau pour garder la trace des valeurs d’in-degré de ces sommets. À l’intérieur de la boucle while, nous devons également visiter tous les sommets et toutes les arêtes. Par conséquent, le temps d’exécution global est .
Recherche en profondeur première
Nous pouvons également utiliser un algorithme de recherche en profondeur première (DFS) pour construire le tri topologique.
4.1. DFS de graphe avec récursion
Avant d’aborder l’aspect tri topologique avec DFS, commençons par passer en revue un algorithme de traversée DFS de graphe standard et récursif :
Dans l’algorithme DFS standard, nous commençons par un sommet aléatoire dans et marquons ce sommet comme visité. Ensuite, nous appelons récursivement la fonction dfsRecursive pour visiter tous ses sommets adjacents non visités. De cette façon, nous pouvons visiter tous les sommets de en temps.
Cependant, puisque nous mettons chaque sommet dans la liste immédiatement lorsque nous le visitons, et puisque nous pouvons commencer à n’importe quel sommet, l’algorithme standard DFS ne peut pas garantir de générer une liste topologiquement triée.
Voyons ce que nous devons faire pour remédier à cette lacune.
4.2. Algorithme de tri topologique basé sur DFS
Nous pouvons modifier l’algorithme DFS pour générer un tri topologique d’un DAG. Pendant la traversée DFS, après que tous les voisins d’un sommet soient visités, nous le plaçons alors en tête de la liste de résultats 
. De cette façon, nous pouvons nous assurer que apparaît avant tous ses voisins dans la liste triée :
Cet algorithme est similaire à l’algorithme DFS standard. Bien que nous commencions toujours avec un sommet aléatoire, nous ne mettons pas le sommet dans la liste immédiatement après l’avoir visité. Au lieu de cela, nous visitons d’abord tous ses voisins de manière récursive, puis nous plaçons le sommet en tête de la liste. Par conséquent, si contient un bord , alors apparaît avant dans la liste.
Le temps d’exécution global est également , car il a la même complexité temporelle que l’algorithme DFS.
Conclusion
Dans cet article, nous avons montré un exemple de tri topologique sur un DAG. Aussi, nous avons discuté de deux algorithmes qui peuvent faire un tri topologique en temps.
L’implémentation Java de l’algorithme de tri topologique basé sur DFS est disponible dans notre article sur Depth First Search in Java.