La diffraction des rayons X est une technique courante de caractérisation des matériaux qui permet d’identifier les orientations des cristaux et l’espacement interatomique. Les rayons X sont utilisés pour cela parce que la longueur d’onde est sur la même échelle de longueur que l’espacement interatomique et les valeurs des paramètres du réseau.
Que se passe-t-il ?
Un rayon X est généré dans un tube à vide en chauffant un filament de tungstène au-delà de sa fonction de travail pour éjecter des électrons. Les conditions de vide sont nécessaires afin d’augmenter le libre parcours moyen des électrons. Les électrons sont accélérés dans une cathode de cuivre avec une énergie de l’ordre de 25 keV. Les collisions des électrons avec la cathode de cuivre entraînent des ionisations de la couche interne, produisant des rayons X lorsque des électrons de plus haute énergie tombent pour remplir la vacance de plus basse énergie. Les électrons de divers niveaux d’énergie supérieurs tombent, produisant des ondes électromagnétiques d’énergie variable. Ainsi, des rayons X de longueurs d’onde multiples (de type K-beta et K-alpha) sont générés. Pour la diffraction des rayons X, l’idéal est d’avoir une lumière monochromatique interagissant avec l’échantillon. Les rayons X de type K-beta sont donc filtrés à l’aide d’une plaque de nickel. Bien qu’il y ait effectivement deux énergies K-alpha associées, les énergies sont si similaires que cela n’affecte pas de manière significative le profil global du pic. Les rayons X passent à travers un collimateur pour ajuster la largeur du faisceau.
Un peu de contexte avec la loi de Bragg
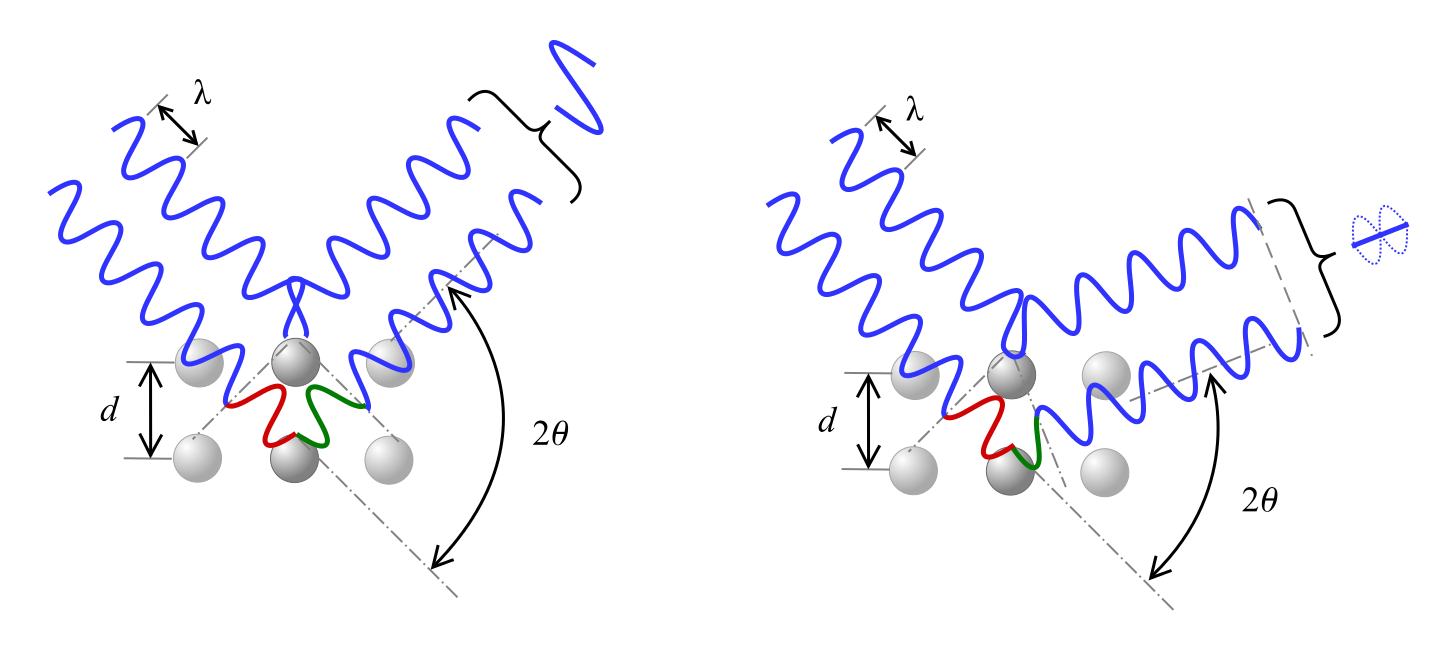
La loi de Bragg décrit la relation pour l’interférence constructive, où les rayons X de longueur d’onde λ incidents sur le matériau à un angle θ sont diffractés par des plans cristallins séparés par la distance d et n représente un nombre entier.
Comme on le voit ci-dessous, un déphasage de l’onde provoque soit une interférence constructive, représentée à gauche, soit une interférence destructive, représentée à droite, selon l’angle 2θ.
Equations pour interpréter les résultats de la DRX
Le compteur, vu ci-dessous dans un schéma d’un diffractomètre à rayons X, est tourné sur une gamme de valeurs 2θ et enregistre l’intensité du signal de rayons X réfléchi par le cristal à chaque position. Cette intensité mesurée en fonction de 2θ est utilisée pour générer un profil de pic.
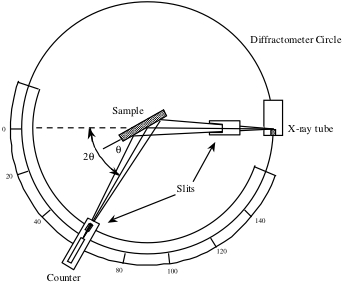
Pour les angles qui satisfont la condition de Bragg, un pic du signal de rayons X sera observé en raison de l’interférence constructive. Ces pics sont ensuite utilisés pour identifier les directions cristallines et calculer les paramètres du réseau. Pour les systèmes cubiques, l’espacement interplanaire, d, peut être calculé par l’équation suivante dérivée de la géométrie du cristal, où a est le paramètre du réseau et h, k, et l sont les indices de Miller.
La combinaison de la loi de Bragg et de l’espacement interplanaire donne l’équation suivante .
Ici, nous avons déplacé toutes les constantes vers le côté gauche de l’équation, ce qui nous permet de comparer les rapports des valeurs de sin2(θ) et des indices de Miller entre différents pics.
Lorsque l’onde électromagnétique incidente frappe le matériau de l’échantillon, les électrons résidant avec le matériau sont perturbés dans un motif oscillant, ce qui génère de nouveaux rayons X et disperse efficacement les ondes lumineuses incidentes. Deux types de diffusion se produisent : la diffusion cohérente ou élastique implique des électrons oscillants étroitement liés qui diffusent des rayons X de la même longueur d’onde, et la diffusion incohérente qui se produit lorsque des électrons peu liés sont mis en mouvement oscillatoire et génèrent des rayons X d’énergie différente. La diffraction des rayons X mesure l’intensité des rayons X diffusés de manière cohérente, qui atteint son maximum là où les ondes interfèrent de manière constructive. Le facteur de diffusion atomique peut être défini comme le rapport entre l’amplitude de l’onde diffusée par un atome et l’amplitude de l’onde diffusée par un électron unique. Ce rapport décrit essentiellement l’efficacité de diffusion d’un atome pour une direction donnée.
Exemple de données XRD
Voici les données recueillies lors d’une expérience que j’ai réalisée pendant mon cours de laboratoire de premier cycle en essayant d’identifier un métal inconnu en fonction de sa structure cristalline.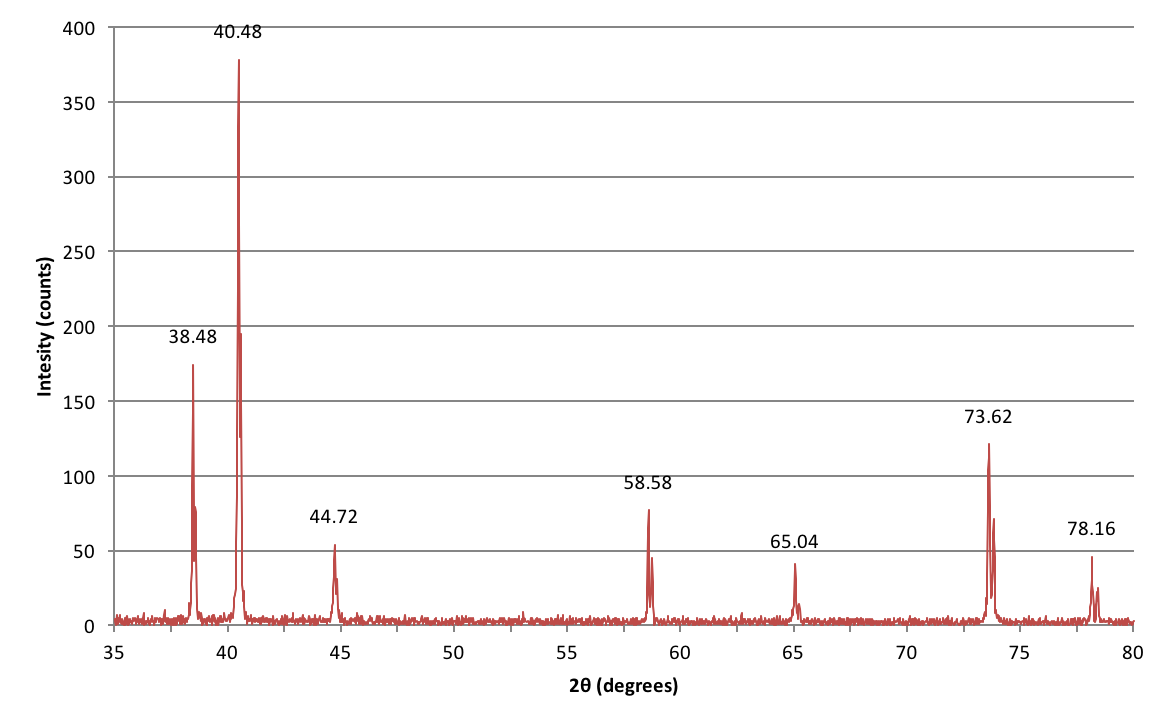
Comment dois-je interpréter ces pics ?
| Structure cristalline | Conditions |
|---|---|
| Simple Cubique | toutes les valeurs h, k, l doivent être égaux |
| Cubique centré sur le corps | h+k+l doivent être égaux |
| Cubique centré sur le visage | h, k, et l doivent être tous impairs ou tous pairs |
Les facteurs de structure tiennent compte des cas où un plan peut exister à mi-chemin entre deux plans voisins et provoquer des interférences destructives. Ces facteurs aboutissent à un ensemble de règles pour différentes géométries de structure cristalline qui déterminent quand l’interférence constructive peut se produire. Le tableau ci-dessus énumère les paramètres de l’indice de Miller dans lesquels l’interférence constructive se produira. Un tableau plus complet est présenté ci-dessous. En comparant les rapports de sin2θ (désignés par $Q^2$ dans le second tableau) pour différents pics de diffraction, la structure cristalline et les indices de Miller peuvent être déterminés.
| Plan cristallin (hkl) | $Q^2$ | Réseaux spatiaux à partir desquels des réflexions sont possibles | |||
|---|---|---|---|---|---|
| 100 | 1 | SC | |||
| 110 | 2 | SC | BCC | ||
| 111 | 3 | SC | FCC | DC | |
| 200 | 4 | SC | BCC | FCC | |
| 210 | 5 | SC | |||
| 211 | 6 | SC | BCC | ||
| – | 7 | ||||
| 220 | 8 | SC | BCC | FCC | DC |
| 300, 221 | 9 | SC | |||
| 310 | 10 | SC | BCC | ||
| 311 | 11 | SC | FCC | DC | |
| 222 | 12 | SC | BCC | FCC | |
| 320 | 13 | SC | |||
| 321 | 14 | SC | BCC | ||
| – | 15 | ||||
| 400 | 16 | SC | BCC | FCC | DC |
X-La diffraction des rayons a une large gamme d’applications pour la caractérisation des matériaux. Elle peut être utilisée comme méthode expérimentale pour déterminer expérimentalement le volume d’une cellule unitaire pour les calculs théoriques de densité. En outre, si le matériau est soumis à une contrainte résiduelle, le réseau déformé présentera une gamme d’espacements d qui satisfont à la loi de Bragg, ce qui entraîne des pics de diffraction beaucoup plus larges. La largeur du pic de diffraction peut également être utilisée pour déterminer la taille des particules.