Les signaux en quadrature, également appelés signaux QI, données QI ou échantillons QI, sont souvent utilisés dans les applications RF. Ils constituent la base de la modulation et de la démodulation des signaux RF complexes, tant au niveau matériel que logiciel, ainsi que de l’analyse des signaux complexes. Ce post examine le concept des signaux IQ et la façon dont ils sont utilisés.
Une paire de signaux périodiques est dite en « quadrature » lorsqu’ils diffèrent en phase de 90 degrés. Le signal « en phase » ou de référence est désigné par « I », et le signal décalé de 90 degrés (le signal en quadrature) est appelé « Q. » Qu’est-ce que cela signifie et pourquoi cela nous intéresse-t-il ? Décortiquons-le en commençant par quelques bases.
Bases de la modulation RF
Je vais commencer par une révision simple de la modulation RF. Une porteuse RF non modulée est simplement une onde sinusoïdale comme indiqué ci-dessous.
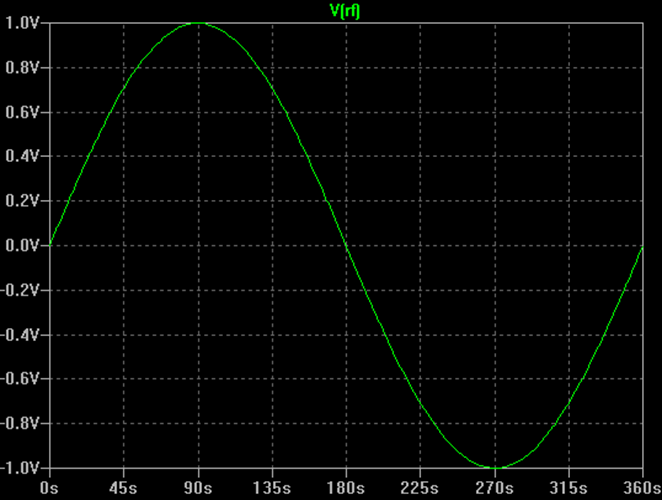
Le signal peut être décrit en fonction du temps par l’équation suivante :
V(t) = A * sin (2 * π * f * t + Ф)
où :
A : est l’amplitude de crête
f : est la fréquence
t : est le temps
Ф : est le déphasage
L’information est « portée » par une porteuse RF grâce au processus de modulation. Le signal d’information (voix, données, etc.) est utilisé pour modifier les propriétés du signal RF. Un exemple simple est la modulation d’amplitude, ou AM.
Pour l’AM, le signal d’information est utilisé pour modifier, ou moduler l’amplitude de la porteuse. Mathématiquement, on peut la représenter en changeant la constante « A » dans l’équation précédente en un certain signal variant dans le temps (le signal d’information) :
V(t) = A(t) * sin (2 * π * f * t + Ф)
Le signal d’information, également appelé signal de bande de base, varie beaucoup plus lentement dans le temps que le signal RF. Par conséquent, pour voir l’effet de la modulation, vous devez observer l’enveloppe du signal RF sur une échelle de temps plus longue, comme indiqué ci-dessous.
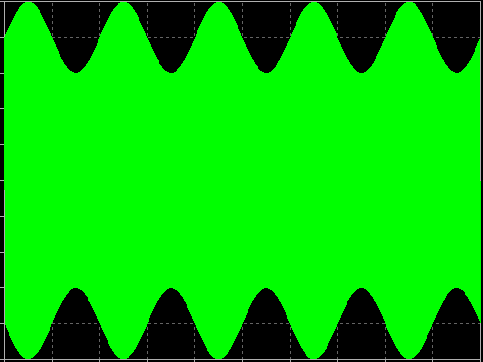
Dans ce cas, le signal A(t) est une sinusoïde. La figure montre comment l’amplitude du signal RF suit le signal sinusoïdal A(t) en bande de base.
Vous pouvez développer ceci en reconnaissant que d’autres propriétés de la porteuse RF peuvent être modifiées, ou modulées, par un signal en bande de base en fonction du temps. Si la fréquence est modulée par un signal en bande de base, vous avez une modulation de fréquence (FM). De même, si la phase est modulée, vous avez alors une modulation de phase (PM). Ainsi :
- A(t) est lorsque l’amplitude varie en fonction du temps
- f(t) est lorsque la fréquence varie en fonction du temps
- Ф(t) est lorsque la phase varie en fonction du temps.
Gardez le concept de base de la modulation à l’esprit lorsque nous lions le concept des signaux en quadrature…
Concepts des signaux en quadrature
Si la différence de phase Ф entre deux sinusoïdes est de 90 degrés (ou π /2 radians), alors ces deux signaux sont dits en quadrature. L’onde sinusoïde et l’onde cosinusoïde en sont un exemple.
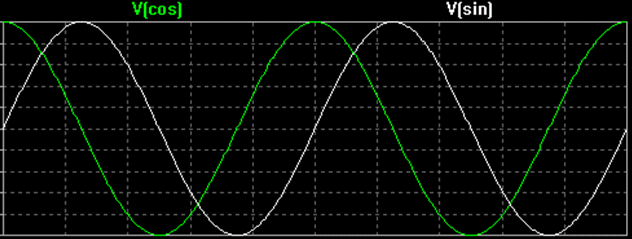
Par convention, l’onde cosinusoïde est la composante en phase et l’onde sinusoïde est la composante en quadrature. La lettre majuscule I représente l’amplitude du signal en phase, et la lettre majuscule Q représente l’amplitude du signal en quadrature.
Utiliser des signaux en quadrature pour moduler
Des choses intéressantes se produisent lorsque vous regardez l’addition de signaux en quadrature.
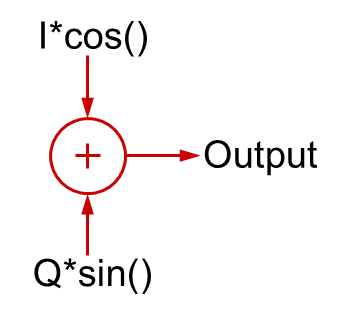
Si I=1 et Q=0, alors vous auriez simplement l’onde cosinus (phase égale à 0). De même, si I=0 et Q=1, vous auriez l’onde sinusoïdale, qui est le signal déphasé de 90 degrés.
Si I et Q étaient tous deux égaux à 1, alors la somme sera un nouveau signal qui est représenté graphiquement ci-dessous.
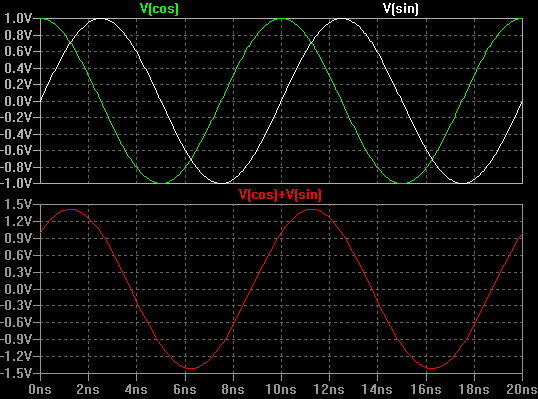
Notez que l’addition de ces deux signaux en quadrature d’amplitude égale donne une nouvelle sinusoïde déphasée de 45 degrés.
Vous pouvez maintenant voir que l’amplitude et la phase de la somme des signaux en quadrature sont fonction de la valeur de I et Q. Par conséquent, vous pouvez créer des signaux RF modulés en faisant varier les valeurs de I et Q en fonction du temps. Examinons quelques exemples.
Exemples de modulation RF numérique
Si Q=0, et que I est modifié entre +1 et -1 au cours du temps, vous créez un signal RF modulé par déplacement de phase binaire (BPSK) :
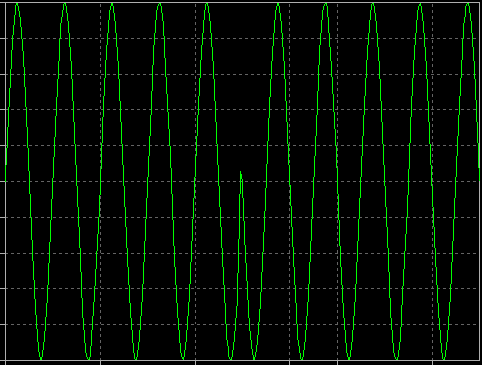
Le signal I(t) pourrait être un simple flux de bits numériques. Si vous faites en sorte que ce signal contrôle le gain de la sinusoïde RF entre +1 et -1, vous avez créé un signal BPSK.
Pour aller plus loin… Si deux bits numériques sont utilisés pour contrôler les valeurs I et Q entre +1 et -1 dans le temps, alors la somme résultante des signaux en quadrature peut être l’une des quatre phases distinctes :
- I=+1 & Q=+1 donne une phase de 45 degrés
- I=-1 & Q=+1 donne une phase de 135 degrés
- I=-1 & Q=-1 donne une phase de 225 degrés
- I=+1 & Q=-1 donne une phase de 315 degrés
C’est ce qu’on appelle la modulation par déplacement de phase en quadrature (QPSK). Ce sont deux exemples de modulation d’amplitude en quadrature (QAM). Les différents états de modulation de la MAQ sont souvent représentés sur un diagramme de constellation. Un diagramme de constellation est simplement un diagramme en phase qui représente l’amplitude et la phase d’un signal sous forme de tracé polaire.
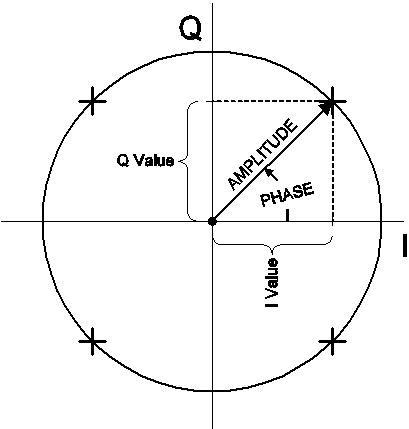
La longueur du vecteur à partir de l’origine représente l’amplitude du signal, et l’angle que forme le vecteur avec l’axe horizontal représente la phase. Les quatre « états » du signal MDPQ décrit ci-dessus sont représentés par les quatre symboles « + » du diagramme. Vous remarquerez également que l’axe horizontal est étiqueté « I » et que l’axe vertical est étiqueté « Q » – car ils représentent les valeurs des composantes I et Q associées au signal.
Les modulations MAQ plus complexes, comme la MAQ16, ont simplement plus d’états. Pour la MAQ16, les valeurs I et Q peuvent chacune avoir une des quatre valeurs discrètes, ce qui donne 16 combinaisons possibles. Il en résulte 16 combinaisons d’amplitude et de phase pour le signal RF.
Signaux en quadrature partout
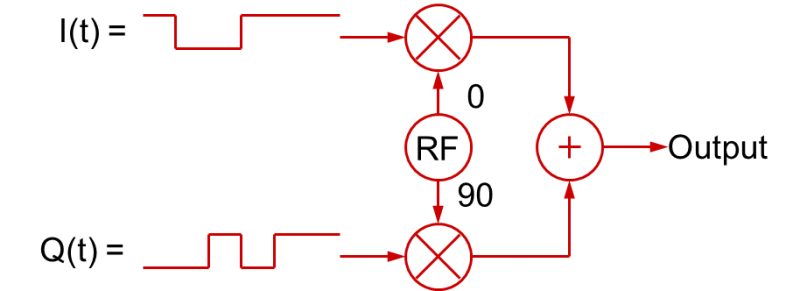
L’utilisation de signaux I et Q qui varient dans le temps pour créer des signaux RF modulés n’est pas limitée aux signaux numériques en bande de base. Les signaux de bande de base I(t) et Q(t) peuvent aussi être des signaux de bande de base analogiques.En fait, dans la plupart des applications RF modulées « numériquement » comme la MDPQ ou la MAQN, les signaux de bande de base sont filtrés pour ralentir les transitions. Ceci est fait pour limiter la largeur de bande résultante du signal RF modulé (les temps de montée/descente numériques rapides occupent beaucoup de largeur de bande !) Ces signaux numériques filtrés sont en fait des signaux analogiques ! Ainsi, dans un sens plus général, le processus de modulation en quadrature peut être illustré comme le montre cette figure :
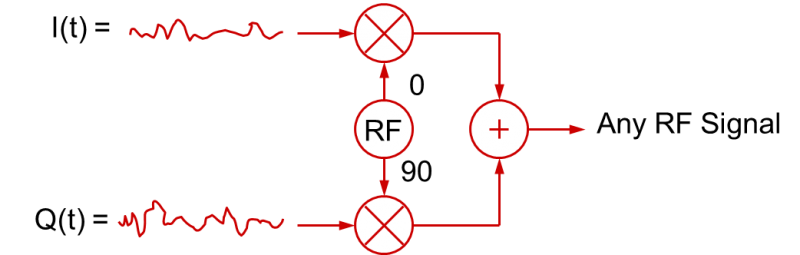
La conclusion générale que vous pouvez en tirer est qu’un signal RF avec n’importe quel type de modulation peut être créé avec les signaux de bande de base I(t) et Q(t) appropriés (qui à leur tour font varier les amplitudes des ondes cosinus et sinus qui sont additionnées).
Bien sûr, le même processus fonctionne en sens inverse pour démoduler un signal RF. En mélangeant un signal RF avec des signaux LO (oscillateur local) en quadrature, on peut créer des signaux en bande de base I(t) et Q(t).
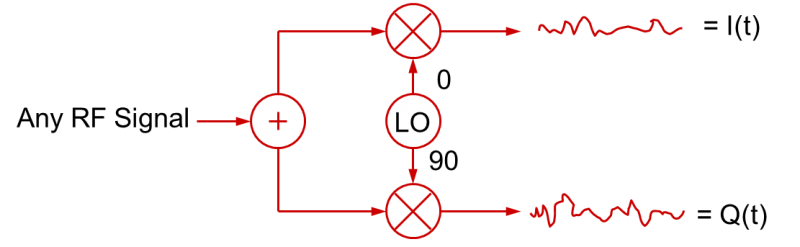
C’est la base fondamentale de la plupart des générations et modulations modernes de signaux RF, ainsi que de la démodulation et de l’analyse des signaux vectoriels.
Les systèmes de radio logicielle (SDR) utilisent largement ces concepts car les signaux I &Q en bande de base sont souvent représentés sous forme de données échantillonnées en temps discret. Par conséquent, le traitement numérique du signal (DSP) peut être utilisé pour définir littéralement les caractéristiques de l’émetteur et du récepteur, notamment le filtrage, la modulation et la démodulation, la CAG, etc. Les récepteurs SDR sont souvent dotés d’une largeur de bande de base de quelques centaines de kHz ou plus, ce qui leur donne la possibilité d’exécuter une grande variété de fonctions, y compris des fonctions de spectrogramme et de bandoscope « large », ainsi que la possibilité de surveiller et de démoduler simultanément plusieurs signaux de différents types.
Les générateurs de signaux vectoriels comportent un modulateur en quadrature qui accepte les signaux I(t) et Q(t) qu’il utilise ensuite pour moduler en amplitude une paire de sinusoïdes en quadrature qui sont ensuite additionnés pour créer la sortie RF modulée. De nombreux générateurs de signaux vectoriels comprennent généralement des prises de panneau où vous pouvez connecter vos propres signaux IQ. Beaucoup comprennent un générateur de formes d’ondes arbitraires (AWG) interne en bande de base pour créer les signaux IQ en bande de base.
Les analyseurs de signaux vectoriels modernes présentent généralement des bandes passantes de 25, 40, 110MHz ou plus. Ils convertissent les signaux RF entrants en leurs composantes I et Q. Toutes les analyses (analyse spectrale en fonction du temps, démodulation, analyse des impulsions, etc.) sont simplement des traitements mathématiques différents sur les mêmes données IQ. Les analyseurs de signaux en temps réel, tels que les séries RSA5000 et RSA6000 de Tektronix, ont la capacité supplémentaire de prendre les flux de données IQ « en direct » et de les traiter en temps réel. Cela ajoute la possibilité de faire des choses comme visualiser le spectre en direct d’un signal RF, ainsi que de pouvoir déclencher sur des événements transitoires qui peuvent n’être visibles que dans le domaine des fréquences.
Voir les dernières offres d’analyseurs de spectre de Tektronix.