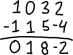Retourner à l’index des leçons | Faire les leçons dans l’ordre | Imprimer la page conviviale
Opérations sur les rangs de la matrice (page 1 de 2)
« Opérations » est le terme mathématicien pour « procédures ». Les quatre « opérations de base » sur les nombres sont l’addition, la soustraction, la multiplication et la division. Pour les matrices, il y a trois opérations de base sur les rangs ; c’est-à-dire qu’il y a trois procédures que vous pouvez faire avec les rangs d’une matrice.
La première opération est le changement de rang. Par exemple, étant donné la matrice :

….vous pouvez intervertir les rangées pour mettre la matrice dans un arrangement de rangées plus agréable, comme ceci:
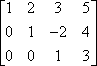
La commutation de rangées est souvent indiquée en dessinant des flèches, comme ceci:

Lorsque vous intervertissez les rangées, faites attention à copier les entrées correctement.
La seconde opération est la multiplication de rangées. Par exemple, étant donné la matrice suivante:

…vous pouvez multiplier la première ligne par -1 pour obtenir une valeur de tête positive dans la première ligne:
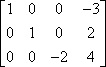
Cette multiplication de ligne est souvent indiquée en utilisant une flèche avec la multiplication listée au-dessus d’elle, comme ceci:
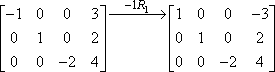
Le « -1R1 » indique l’opération réelle. Le « -1 » indique que nous avons multiplié par le chiffre négatif un ; le « R1 » indique que nous travaillions avec la première ligne. Notez que les deuxième et troisième rangées ont été copiées, sans modification, dans la deuxième matrice. La multiplication ne s’est appliquée qu’à la première ligne, donc les entrées des deux autres lignes ont juste été reportées sans modification.
Vous pouvez multiplier par ce que vous voulez. Par exemple, pour obtenir un 1 de tête dans la troisième ligne de la matrice précédente, vous pouvez multiplier la troisième ligne par un demi négatif :

Puisque vous ne faisiez rien avec les première et deuxième lignes, ces entrées étaient juste copiées sans modification dans la nouvelle matrice.
Vous pouvez faire plus d’une multiplication de lignes dans la même étape, donc vous auriez pu faire les deux étapes ci-dessus en une seule étape, comme ceci:
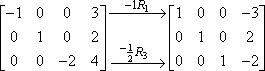
C’est une bonne idée d’utiliser une certaine forme de notation (comme les flèches et les indices ci-dessus) afin de pouvoir garder une trace de votre travail. Les matrices sont très désordonnées, surtout si vous les faites à la main, et les notes peuvent faciliter la vérification de votre travail plus tard. Cela impressionnera également votre professeur.
La dernière opération de ligne est l’addition de ligne. L’addition de rangée est similaire à la méthode « d’addition » pour résoudre les systèmes d’équations linéaires. Supposons que vous ayez le système d’équations suivant :
x + 3y = 1
-x + y = 3 Copyright © Elizabeth Stapel 2003-2011 Tous droits réservés
Avertissement
Vous pourriez commencer à résoudre ce système en ajoutant vers le bas les colonnes pour obtenir 4y = 4 :
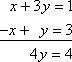
Vous pouvez faire quelque chose de similaire avec les matrices.Par exemple, étant donné la matrice suivante:

…vous pouvez « réduire » (obtenir plus de zéros de tête dans) la deuxième ligne en y ajoutant la première ligne (le but général avec les matrices à ce stade étant d’obtenir un « 1 » – ou des « 0 » puis un « 1 » – au début de chaque ligne de la matrice). Lorsque vous réduisiez le système linéaire à deux équations par addition, vous avez dessiné une barre d’égalité en bas et ajouté vers le bas. Lorsque vous utilisez l’addition sur une matrice, vous devez prendre du papier brouillon, car vous ne voulez pas essayer de faire le travail à l’intérieur de la matrice. Ajoutez donc les deux lignes sur votre papier brouillon:
|
Travail brouillon – |
|
C’est votre nouvelle deuxième ligne ; vous l’écrirez à la place de l’ancienne. Le résultat ressemblera à ceci:
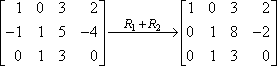
Dans ce cas, le « R1 + R2 » sur la flèche signifie « j’ai ajouté la ligne un à la ligne deux, et c’est le résultat que j’ai obtenu ». Puisque la ligne un n’a pas réellement changé, et puisque nous n’avons rien fait avec la ligne trois, ces lignes sont copiées dans la nouvelle matrice sans modification.
Top | 1 | 2 | Retour à l’index suivant >>
|
Citer cet article comme: |
Stapel, Elizabeth. » Opérations sur les rangs de la matrice « . Purplemath. Disponible à partir de 2016
|
.