Prérequis – Graph Theory Basics – Set 1
Un graphe est une structure équivalente à un ensemble d’objets dans lequel certaines paires d’objets sont en quelque sorte « reliées ». Les objets du graphe correspondent aux sommets et les relations entre eux correspondent aux arêtes. Un graphe est représenté schématiquement comme un ensemble de points représentant des sommets reliés par des lignes ou des courbes représentant des arêtes.
Formellement,
« Un graphe 
consiste en 
, un ensemble non vide de sommets (ou nœuds) et 
, un ensemble d’arêtes. Chaque arête a soit un ou deux sommets associés, appelés ses points d’extrémité. »
Types de graphes :Il existe plusieurs types de graphes distingués sur la base des arêtes, de leur direction, de leur poids etc.
1. Graphe simple – Un graphe dans lequel chaque arête relie deux sommets différents et où aucune arête ne relie la même paire de sommets est appelé un graphe simple. Par exemple, considérons le graphe suivant –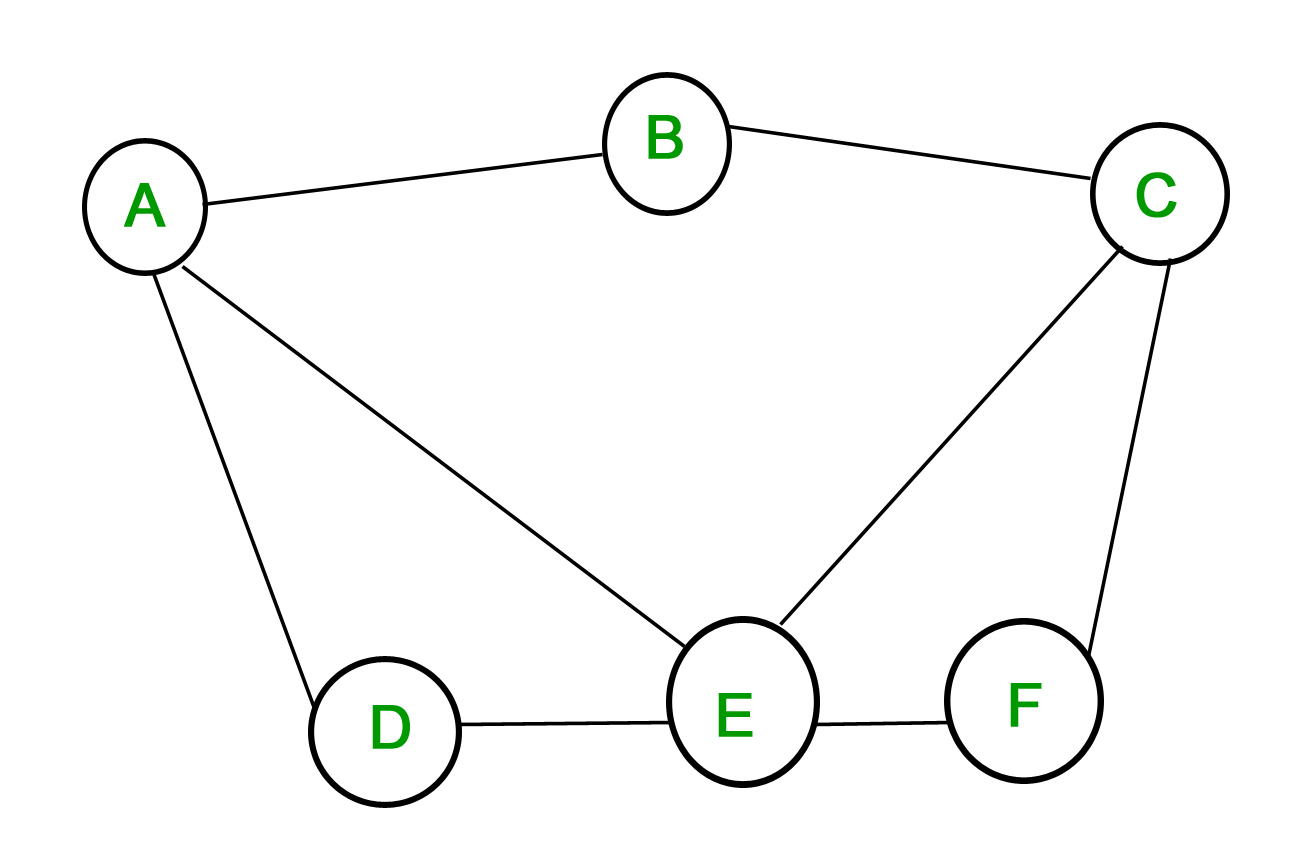
Le graphe ci-dessus est un graphe simple, puisqu’aucun sommet n’a d’auto-boucle et que deux sommets n’ont pas plus d’une arête les reliant.
Les arêtes sont désignées par les sommets qu’elles relient- 
est l’arête reliant les sommets 
et 
.
2. Multigraphe – Un graphe dans lequel plusieurs arêtes peuvent connecter la même paire de sommets est appelé un multigraphe.
Puisqu’il peut y avoir plusieurs arêtes entre la même paire de sommets, la multiplicité de l’arête indique le nombre d’arêtes entre deux sommets.
Le graphe ci-dessus est un multigraphe puisqu’il y a plusieurs arêtes entre et 
. La multiplicité de l’arête 
est 2.
Dans certains graphes, contrairement à ceux présentés ci-dessus, les arêtes sont dirigées. Cela signifie que la relation entre les objets est uniquement à sens unique et non à double sens. La direction des arêtes peut être importante dans certaines applications.
Selon que les arêtes sont dirigées ou non, nous pouvons avoir des graphes dirigés et des graphes non dirigés. Cette propriété peut être étendue aux graphes simples et aux multigraphes pour obtenir des graphes simples dirigés ou non dirigés et des multigraphes dirigés ou non dirigés.
Terminologie de base des graphes :
Dans la discussion ci-dessus, certains termes concernant les graphes ont déjà été expliqués comme les sommets, les arêtes, les arêtes dirigées et non dirigées, etc. Il existe d’autres termes qui décrivent les propriétés des sommets et des arêtes.
- Adjacence – Dans un graphe
, deux sommets 
et 
sont dits adjacents s’ils sont les extrémités d’une arête. On dit que l’arête 
est incidente avec les sommets.
Dans le cas où l’arête est dirigée, on dit que est adjacente à et que est adjacente de . Ici, est dit sommet intitial et est dit sommet terminal. - Degré – Le degré d’un sommet est le nombre d’arêtes qui lui sont incidentes, à l’exception de l’auto-boucle qui contribue deux fois au degré du sommet. Le degré d’un sommet est noté
.
Dans le cas des graphes dirigés, le degré est encore classé en in-degré et out-degré. Le in-degré d’un sommet est le nombre d’arêtes avec le sommet donné comme sommet terminal. Le degré de sortie d’un sommet est le nombre d’arêtes dont le sommet donné est le sommet initial. Le degré d’entrée est noté
et le degré de sortie est noté 
.
Par exemple, dans le graphe dirigé illustré ci-dessus représentant les vols entre les villes, le degré d’entrée du sommet « Delhi » est 3 et son degré de sortie est également 3.
Note : Si un sommet a un degré nul, il est appelé isolé. Si le degré est de un alors il est appelé pendant.
Théorème du tremblement de mains :
Qu’obtiendrait-on si on additionnait les degrés de tous les sommets d’un graphe. Dans le cas d’un graphe non orienté, chaque arête contribue deux fois, une fois pour son sommet initial et une seconde pour son sommet terminal. La somme des degrés est donc égale à deux fois le nombre d’arêtes. Ce fait est énoncé dans le théorème du handshaking.
Let be an undirected graph with edges. ThenIn case G is a directed graph,
Le théorème du handshaking, pour les graphes non orientés, a un résultat intéressant –
An undirected graph has an even number of vertices of odd degree.
Proof : Soit 
et 
les ensembles de sommets de degrés pairs et impairs respectivement.
Nous savons par le théorème de la poignée de main que,
Donc,
La somme des degrés des sommets de degrés pairs est paire. Le LHS est également pair, ce qui signifie que la somme des degrés des sommets avec des degrés impairs doit être paire.
Donc, le nombre de sommets avec un degré impair est pair.
Certains graphes simples spéciaux :
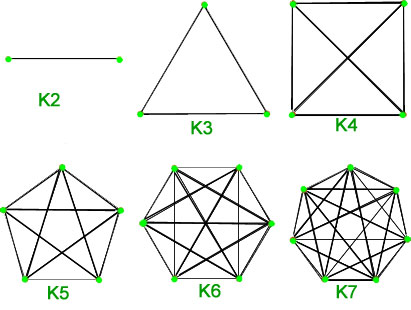
1. Graphes complets – Un graphe simple de 
sommets ayant exactement une arête entre chaque paire de sommets est appelé un graphe complet. Un graphe complet de sommets est noté 
. Le nombre total d’arêtes est n*(n-1)/2 avec n sommets dans le graphe complet.
2. Cycles – Les cycles sont des graphes simples avec des sommets 
et des arêtes 
. Un cycle avec sommets est noté 
. Le nombre total d’arêtes est n avec n sommets dans le graphe du cycle.
3. Roues – Une roue est comme un cycle, avec un sommet supplémentaire qui est connecté à tous les autres sommets. Les roues de sommets avec 1 sommet supplémentaire sont désignées par 
. Le nombre total d’arêtes est de 2*(n-1) avec n sommets dans le graphe de roue.
4. Hypercube – L’hypercube ou n-cube est un graphe avec 
sommets représentés chacun par une chaîne de n bits. Les sommets qui diffèrent d’au plus 1 bit sont reliés par des arêtes. Un hypercube de sommets est noté 
. Le nombre total d’arêtes est n*
avec sommets dans le graphe cube.
5. Graphes bipartites – Un graphe simple est dit bipartite si son ensemble de sommets peut être divisé en deux ensembles disjoints tels que chaque arête dans a son sommet initial dans le premier ensemble et le sommet terminal dans le second ensemble. Le nombre total d’arêtes est de (n*m) avec (n+m) sommets dans un graphe bipartite.
Théorème – Un graphe simple est bipartite si et seulement s’il est possible d’attribuer une de deux
couleurs différentes à chaque sommet du graphe de sorte qu’il n’y ait pas deux adjacents qui se voient attribuer la
même couleur.
Un graphe bipartite avec 
et sommets dans ses deux sous-ensembles disjoints est dit complet s’il existe une arête de chaque sommet du premier ensemble à chaque sommet du second ensemble, pour un total de 
arêtes. Un graphe biparti complet avec sommets dans le premier ensemble et sommets dans le second ensemble est noté 
.
GATE CS Corner Questions
La pratique des questions suivantes vous aidera à tester vos connaissances. Toutes les questions ont été posées au GATE au cours des années précédentes ou lors des tests blancs du GATE. Il est fortement recommandé de les pratiquer.
1. GATE CS 2013, Question 25
2. GATE CS 2014 Set-1, Question 61
3. GATE CS 2006, Question 71
4. GATE CS 2002, Question 25
5. GATE CS 2004, Question 37
6. GATE CS 2014 Set-2, Question 13
Références-
Graphes – Wikipédia
Mathématiques discrètes et ses applications, par Kenneth H Rosen
Cet article est contribué par Chirag Manwani. Si vous aimez GeeksforGeeks et souhaitez contribuer, vous pouvez également écrire un article en utilisant contribute.geeksforgeeks.org ou envoyer votre article par courrier à [email protected]. Voyez votre article apparaître sur la page principale de GeeksforGeeks et aidez d’autres Geeks.