- La connectivité est un concept de base de la théorie des graphes. Elle définit si un graphe est connecté ou déconnecté. Sans connectivité, il n’est pas possible de parcourir un graphe d’un sommet à un autre sommet.
- Un graphe est dit connecté s’il existe un chemin entre chaque paire de sommet. De chaque sommet à tout autre sommet, il doit y avoir un chemin à parcourir. C’est ce qu’on appelle la connectivité d’un graphe.
- Un graphe est dit déconnecté, s’il existe plusieurs sommets et arêtes déconnectés.
- Les théories de la connectivité des graphes sont essentielles dans les applications de réseaux, le routage des réseaux de transport, la tolérance des réseaux, etc.
Exemple
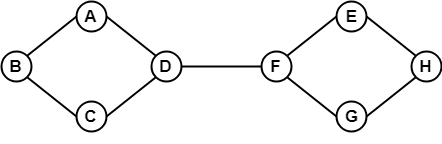
Dans l’exemple ci-dessus, il est possible de voyager d’un sommet à un autre sommet. Ici, nous pouvons traverser du sommet B à H en utilisant le chemin B -> A -> D -> F -> E -> H. Par conséquent, c’est un graphe connecté.
Exemple
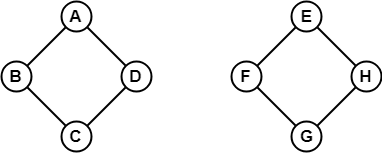
Dans l’exemple ci-dessus, il n’est pas possible de traverser du sommet B à H car il n’y a pas de chemin entre eux directement ou indirectement. Par conséquent, c’est un graphe déconnecté.
Voyons quelques concepts de base de la connectivité.
Vertex coupé
Un sommet unique dont la suppression déconnecte un graphe est appelé un sommet coupé.
Laissons G être un graphe connecté. Un sommet v de G est appelé un sommet coupé de G, si G-v (Enlever v de G) résulte un graphe déconnecté.
Lorsque nous enlevons un sommet d’un graphe, alors le graphe se casse en deux ou plusieurs graphes. Ce sommet est appelé un sommet coupé.
Note : Soit G un graphe avec n sommets :
- Un graphe connecté G peut avoir au maximum (n-2) sommets coupés.
- Supprimer un sommet coupé peut laisser un graphe déconnecté.
- La suppression d’un sommet peut augmenter le nombre de composantes d’un graphe d’au moins un.
- Chaque sommet non-pendant d’un arbre est un sommet coupé.
Exemple 1

Exemple 2
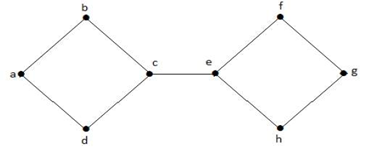
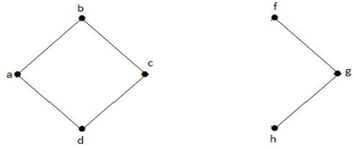
Dans le graphe ci-dessus, le sommet ‘e’ est un sommet coupé. Après avoir enlevé le sommet ‘e’ du graphe ci-dessus, le graphe deviendra un graphe déconnecté.
Cut Edge (Bridge)
Un cut- Edge ou bridge est une arête unique dont l’enlèvement déconnecte un graphe.
Let G est un graphe connecté. Une arête e de G est appelée arête coupée de G, si G-e (Enlever e de G) résulte un graphe déconnecté.
Lorsque nous enlevons une arête d’un graphe, alors le graphe se casse en deux ou plusieurs graphes. Cette arête de retrait est appelée arête coupée ou pont.
Note : Soit G un graphe avec n sommets :
- Un graphe connecté G peut avoir au plus (n-1) arêtes coupées.
- Retirer une arête coupée peut laisser un graphe déconnecté.
- La suppression d’une arête peut augmenter le nombre de composants d’un graphe d’au plus un.
- Une arête coupée ‘e’ ne doit pas être la partie d’un cycle quelconque dans G.
- Si une arête coupée existe, alors un sommet coupé doit aussi exister car au moins un sommet d’une arête coupée est un sommet coupé.
- Si un sommet coupé existe, alors l’existence de toute arête coupée n’est pas nécessaire.
Exemple 1
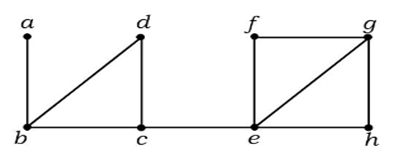
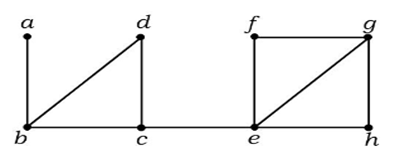
Dans le graphe ci-dessus, l’arête (c, e) est une arête coupée. Après avoir retiré cette arête du graphe ci-dessus, le graphe deviendra un graphe déconnecté.
Exemple 2
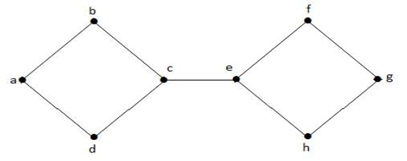
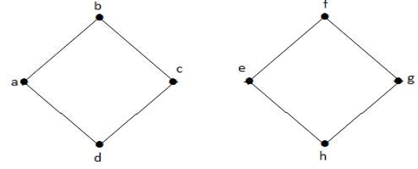
Dans le graphe ci-dessus, l’arête (c, e) est une arête coupée. Après avoir retiré cette arête du graphe ci-dessus, le graphe deviendra un graphe déconnecté.
Ensemble coupé
Dans un graphe connecté G, un ensemble coupé est un ensemble S d’arêtes ayant les propriétés suivantes :
- La suppression de toutes les arêtes de S déconnecte G.
- La suppression de certaines des arêtes (mais pas toutes) dans S ne déconnecte pas G.
Exemple 1
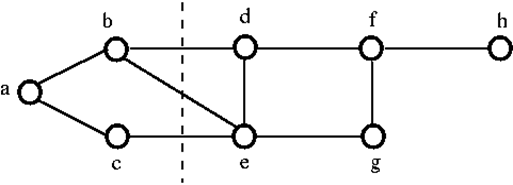
Pour déconnecter le graphe G ci-dessus, nous devons supprimer les trois arêtes, c’est-à-dire bd, be et ce. On ne peut pas le déconnecter en supprimant seulement deux des trois arêtes. Par conséquent, {bd, be, ce} est un ensemble coupé.
Après avoir retiré l’ensemble coupé du graphe ci-dessus, il se présenterait comme suit :
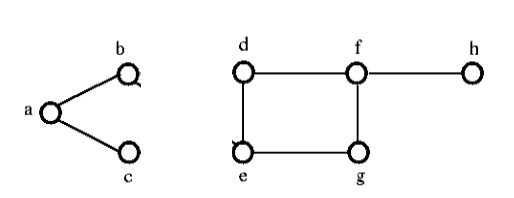
Connectivité des arêtes
La connectivité des arêtes d’un graphe connecté G est le nombre minimum d’arêtes dont le retrait rend G déconnecté. Elle est notée par λ(G).
Lorsque λ(G) ≥ k, alors le graphe G est dit être connecté par k arêtes.
Exemple
Voyons un exemple,
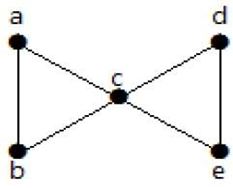
Du graphe ci-dessus, en enlevant deux arêtes minimales, le graphe connecté devient un graphe déconnecté. Par conséquent, sa connectivité des arêtes est 2. Donc le graphe ci-dessus est un graphe connecté à deux arêtes.
Voici les quatre façons suivantes de déconnecter le graphe en enlevant deux arêtes:
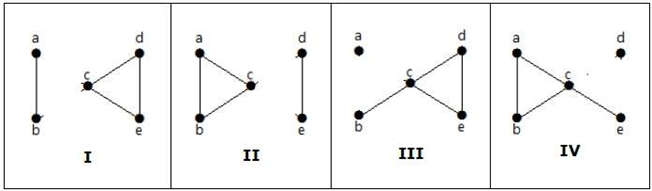
Connectivité des sommets
La connectivité (ou connectivité des sommets) d’un graphe connecté G est le nombre minimum de sommets dont l’enlèvement fait que G se déconnecte ou se réduit à un graphe trivial. Elle est dénotée par K(G).
Le graphe est dit k- connecté ou k-vertex connecté lorsque K(G) ≥ k. Pour enlever un sommet, on doit aussi enlever les arêtes qui lui sont incidentes.
Exemple
Voyons un exemple :
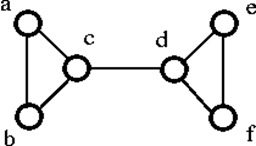
Le graphe G ci-dessus peut être déconnecté par la suppression du seul sommet soit ‘c’ soit ‘d’. Par conséquent, sa connectivité de sommet est de 1. Par conséquent, c’est un graphe à connexion 1.
.