Chaque fois que nous discutons de la prédiction des modèles, il est important de comprendre les erreurs de prédiction (biais et variance). Il existe un compromis entre la capacité d’un modèle à minimiser le biais et la variance. Acquérir une bonne compréhension de ces erreurs nous aiderait non seulement à construire des modèles précis, mais aussi à éviter l’erreur de surajustement et de sous-ajustement.
Donc, commençons par les bases et voyons comment elles font la différence pour nos modèles d’apprentissage automatique.
Qu’est-ce que le biais ?
Le biais est la différence entre la prédiction moyenne de notre modèle et la valeur correcte que nous essayons de prédire. Un modèle avec un biais élevé accorde très peu d’attention aux données d’entraînement et simplifie trop le modèle. Il conduit toujours à une erreur élevée sur les données de formation et de test.
Qu’est-ce que la variance ?
La variance est la variabilité de la prédiction du modèle pour un point de données donné ou une valeur qui nous indique la propagation de nos données. Un modèle avec une variance élevée accorde beaucoup d’attention aux données d’entraînement et ne généralise pas sur les données qu’il n’a pas vues auparavant. Par conséquent, de tels modèles sont très performants sur les données d’entraînement mais ont des taux d’erreur élevés sur les données de test.
Mathématiquement
Détachons la variable que nous essayons de prédire comme Y et les autres covariables comme X. Nous supposons qu’il existe une relation entre les deux telle que
Y=f(X) + e
Où e est le terme d’erreur et il est normalement distribué avec une moyenne de 0.
Nous ferons un modèle f^(X) de f(X) en utilisant la régression linéaire ou toute autre technique de modélisation.
Donc l’erreur quadratique attendue en un point x est
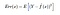
L’erreur quadratique attendue. Err(x) peut être encore décomposée comme suit

Err(x) est la somme du Bias², de la variance et de l’erreur irréductible.
L’erreur irréductible est l’erreur qui ne peut pas être réduite en créant de bons modèles. C’est une mesure de la quantité de bruit dans nos données. Ici, il est important de comprendre que peu importe la qualité de notre modèle, nos données auront une certaine quantité de bruit ou d’erreur irréductible qui ne peut pas être supprimée.
Bias et variance en utilisant le diagramme de l’œil de taureau

Dans le diagramme ci-dessus, le centre de la cible est un modèle qui prédit parfaitement les valeurs correctes. Au fur et à mesure que nous nous éloignons du centre de la cible, nos prédictions deviennent de plus en plus mauvaises. Nous pouvons répéter notre processus de construction de modèles pour obtenir des succès séparés sur la cible.
Dans l’apprentissage supervisé, l’underfitting se produit lorsqu’un modèle incapable de capturer le modèle sous-jacent des données. Ces modèles ont généralement un biais élevé et une faible variance. Cela se produit lorsque nous avons très peu de données pour construire un modèle précis ou lorsque nous essayons de construire un modèle linéaire avec des données non linéaires. En outre, ce type de modèles est très simple pour capturer les modèles complexes dans les données comme la régression linéaire et logistique.
Dans l’apprentissage supervisé, l’overfitting se produit lorsque notre modèle capture le bruit en même temps que le modèle sous-jacent dans les données. Cela se produit lorsque nous entraînons beaucoup notre modèle sur un ensemble de données bruyantes. Ces modèles ont un faible biais et une variance élevée. Ces modèles sont très complexes comme les arbres de décision qui sont sujets à l’overfitting.

Pourquoi le compromis biais-variance ?
Si notre modèle est trop simple et a très peu de paramètres alors il peut avoir un biais élevé et une faible variance. D’autre part, si notre modèle a un grand nombre de paramètres alors il aura une variance élevée et un biais faible. Donc, nous devons trouver le bon/bon équilibre sans sur-adapter et sous-adapter les données.
Ce compromis dans la complexité est la raison pour laquelle il y a un compromis entre le biais et la variance. Un algorithme ne peut pas être plus complexe et moins complexe en même temps.
Erreur totale
Pour construire un bon modèle, nous devons trouver un bon équilibre entre le biais et la variance de telle sorte qu’il minimise l’erreur totale.


Un équilibre optimal entre biais et variance ne surajusterait ou ne sous-ajusterait jamais le modèle.
Par conséquent, la compréhension du biais et de la variance est essentielle pour comprendre le comportement des modèles de prédiction.
Merci de votre lecture!