Combien de côtés a un cercle ?

C’est une question de devoir d’école primaire qui provoque des désaccords chez les mathématiciens chevronnés. Afin de trouver la bonne réponse, j’ai fait appel au plus rigoureux des instruments scientifiques, le sondage Twitter :

A posteriori, je regrette de ne pas avoir inclus une option « aucune des réponses ci-dessus », mais nous y reviendrons plus tard. Dans ce billet, je vais passer en revue ces trois réponses (et « Aucune des réponses ci-dessus »), et discuter de leurs avantages et inconvénients tels que je les vois, avant de révéler de façon spectaculaire la bonne réponse.

Mais d’abord : pourquoi ne pouvons-nous pas donner directement la bonne réponse ? Les mots de la question ne sont guère mystérieux. Nous savons tous ce qu’est un « cercle », ce que signifie compter « combien » de quelque chose, et ce qu’est un « côté »… ou pas ? Voici les définitions (approximatives) que j’ai distillées lors de discussions avec deux élèves de l’école primaire qui avaient été confrontés à cette question :

1. Une ligne faisant partie de la limite d’une forme d’une figure plane.

Le but de dire figure plane plutôt que « forme » ici est que nous voulons des formes qui vivent en 2 dimensions (par exemple des carrés ou des cercles, mais pas des sphères ou des cubes). La question suivante est de savoir ce qu’est une « ligne » dans la définition 1. Voici une variante qui épingle cela:

2. Une ligne droite faisant partie de la limite d’une figure plane.

Si vous tapez « define : side » dans Google, la définition la plus pertinente est:

Une figure rectiligne est une figure construite à partir de lignes droites. Cette définition est donc un raffinement de la définition 2, et nous permet d’affirmer qu’un carré a quatre côtés, mais à première vue, elle n’a rien à dire sur les figures planes non rectilignes telles que les cercles.

Un nombre infini de côtés ?

Je pense qu’il est fort à parier que les personnes ayant répondu à mon sondage Twitter ont un niveau d’éducation mathématique plus élevé que la moyenne nationale. Le fait qu’ils aient été divisés sur cette question du tout, et qu’une petite majorité ait choisi une réponse qui est assez bien indisponible pour le public habituel de cette question (les élèves de l’école primaire), suggère certainement que quelque chose ne va pas quelque part.

Alors, un cercle a-t-il une infinité de côtés ? Il est définitivement utile de considérer un cercle comme la limite des polygones à n côtés lorsque n devient de plus en plus grand. C’est exactement l’approche qu’Archimède, Liu Hui et d’innombrables autres personnes ont utilisée au cours des siècles pour étudier la géométrie circulaire, y compris pour trouver des approximations pour π.

Une édition de la dynastie Ming du XVIe siècle du Jiuzhang suanshu (Neuf chapitres sur l’art mathématique), troisième siècle de notre ère.

Parfois, il est absolument judicieux, comme un raccourci pratique, de penser à un cercle comme étant comme un polygone avec une infinité de côtés.

Mais, en tant que pédant insupportable un mathématicien, je voudrais distinguer entre le raccourci pratique et la vérité littérale. Si nous sommes inflexibles sur le fait qu’un cercle est vraiment un polygone avec une infinité de côtés, alors la question se pose : quels sont les côtés ? Et la seule réponse plausible est certainement : les points individuels du cercle. Quelle est la longueur de ces soi-disant côtés ? Zéro centimètre. Et ces côtés sont-ils séparés par des angles ? Pas apparemment, soit il n’y a pas de coins du tout, soit chaque point est à la fois un côté et un coin.

Je dirais que les côtés de longueur zéro sont… un concept problématique. Comment pouvez-vous dire si vous en avez ? Par exemple, supposons que j’étudie un système où un carré apparaît comme une limite d’octogones comme ceci :

Dans cette situation, il pourrait bien être logique pour moi de penser à mon carré comme ayant huit côtés, dont quatre de longueur zéro. Mais si j’insistais pour dire que mon carré (parfaitement ordinaire) a vraiment huit côtés, vous pourriez hausser un sourcil.

Donc, cette réponse – la gagnante de mon sondage – est la seule que je vais déclarer définitivement fausse, alors que c’est aussi la seule qui offre un quelconque aperçu géométrique. Un paradoxe ? Pas vraiment. Raisonner par analogie est une compétence précieuse en mathématiques et dans la vie ; en même temps, il est important de s’accrocher à la réalisation que c’est ce que nous faisons.

Pour une infinité de côtés : géométriquement éclairant.
Contre une infinité de côtés : des carrés à huit côtés.

Sur une tangente 1 : les apeirogons

Même si un cercle n’en est pas un, existe-t-il des choses comme des polygones avec une infinité de côtés ? Eh bien, il existe un mot pour décrire une telle chose un apeirogon. Un apeirogon régulier aurait alors des côtés de longueur égale (non nulle) avec des angles égaux entre eux. La seule option ici est cet objet stupéfiamment peu excitant:

Si vous vous opposez à ce que ce soit un « polygone » (soit bcause des angles de 180° ou de la chaîne d’arêtes ne se fermant pas en boucle), que diriez-vous de quelque chose comme ceci : commencez au bas d’un cercle, et à chaque étape déplacez-vous autour de la moitié de ce qui reste du cercle, et remplacez l’arc que vous venez de parcourir par une arête droite :

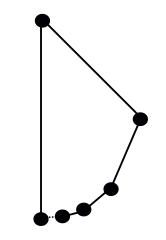
Est-ce un véritable polygone ? Une fois de plus, cela dépend de vos termes. Selon une définition courante, celle d’une « chaîne polygonale fermée », ceci ne remplit pas les conditions requises puisque le coin de départ (en bas à gauche) ne se connecte qu’à une seule arête. Mais il s’en faut de peu : ce point est la limite d’une séquence d’arêtes provenant de la droite, ce qui fait de cette forme une « courbe fermée linéaire par morceaux non auto-intersectée », une autre définition du polygone que les gens utilisent.

Si nous quittons notre monde euclidien habituel et entrons dans l’espace hyperbolique, alors il n’y a aucune ambiguïté. Les apérions (même les apérions réguliers) existent tout simplement:

Un pavage du plan hyperbolique par des apérions réguliers. (Par Anton Sherwood – Œuvre propre, Domaine public, https://commons.wikimedia.org/w/index.php?curid=13260274 )

Sur une tangente 2 : les points extrêmes

Il pourrait être plus défendable de dire qu’un cercle a une infinité de coins qu’une infinité de côtés (bien que ce ne soit pas une question qui semble être posée très souvent). Pour commencer, si un coin d’un carré est un point où sa ligne de délimitation n’est pas droite, alors chaque point du cercle satisfait à cette condition. De manière plus sophistiquée, il existe une notion de point extrême d’une forme : c’est tout point par lequel on peut tracer un segment de ligne droite qui ne touche la forme qu’en ce point précis. Pour un carré et de nombreuses formes familières, les points extrêmes coïncident exactement avec les coins. Chaque point sur la limite du cercle est un point extrême, donc il est certainement vrai qu’un cercle en a une infinité.

On pourrait s’inquiéter du fait que certaines formes comme ce chevron ont des coins qui ne sont pas des points extrêmes:

Ici le coin central inférieur n’est pas un point extrême (les trois autres coins le sont). Ce qui ne va pas, c’est que cette forme n’est pas convexe (en gros, elle a des bouts qui dépassent trop). Un cercle est convexe, il n’y a donc pas lieu de s’inquiéter. On pourrait aussi remédier à la situation en définissant un « coin » comme étant un point extrême soit de la forme en question, soit de son complément, c’est-à-dire le plan entier dans lequel la forme est découpée. Cette approche permettrait de détecter les coins de tous les polygones, y compris le chevron. Pour les courbes lisses, elle identifierait tous les points limites comme des « coins », à l’exception des points d’inflexion (ce qui n’est pas déraisonnable puisque nous pourrions soutenir que la frontière est droite à cet endroit).

Un côté ?

À l’école primaire, il semble que « un » soit la réponse qui obtient la coche. Et il y a une justification modérément décente. Rappelez-vous la définition 1 ci-dessus :

1. Une ligne faisant partie de la limite d’une figure plane.

La question immédiate est de savoir ce qui compte comme une « ligne », surtout si nous n’insistons pas sur la rectitude. Si nous sommes trop détendus à ce sujet, alors toute figure plane pourrait être dite avoir « un côté », dans le même sens qu’elle a une frontière, un périmètre ou une circonférence. Mais cela doit être faux, car nous voulons sûrement qu’un carré en ait quatre. Eh bien, un carré a quatre points où il n’est pas lisse, avec quatre sections lisses entre les deux. Peut-être que c’était vraiment les sections lisses que nous comptions depuis le début. Nous avons donc implicitement un nouveau raffinement de la définition 1 (et profitons également de l’occasion pour abandonner le terme vague de « figure ») :

4. Chaque section lisse d’une courbe fermée lisse par morceaux.

Une « courbe fermée » est une courbe qui s’enroule autour d’elle-même pour se rencontrer, de sorte qu’elle n’a pas d’extrémités libres. « Piecewise-smooth » signifie qu’elle est construite à partir de sections lisses, qui se rencontrent en des points isolés non lisses. Il est parfaitement légitime de vouloir compter les sections lisses de la frontière d’une telle forme, et il n’est en aucun cas scandaleux d’utiliser le mot « côté » pour le faire. Donc je ne dis certainement pas que c’est définitivement la mauvaise réponse.

La question est de savoir si cette interprétation de « côté » n’est pas simplement cohérente, mais suffisamment naturelle pour qu’elle puisse simplement être présumée sans être énoncée explicitement (ce qui est rarement, voire jamais, le cas). Que se passe-t-il lorsque la douceur et la rectitude s’accordent différemment ? Considérez cette forme de pierre tombale, créée en remplaçant le haut d’un carré par un demi-cercle de diamètre égal.

Cette forme a deux sections lisses (la ligne du bas et le reste) mais trois bords droits (plus une pièce incurvée joignant deux d’entre eux de manière lisse). Alors, combien de côtés a-t-il ? J’ai à nouveau consulté mes amis de Twitter :

Cette fois, j’aurais dû inclure « infiniment nombreux » comme option, bien que cela puisse être absorbé dans « Aucune des réponses ci-dessus ». Toute personne votant que le cercle a une infinité de côtés devrait automatiquement voter « Aucun de ce qui précède » ici, à moins que – une mise en garde importante – la nature de cette forme indique au lecteur une notion différente de « côté ». Le fait que les choix les plus populaires dans ces deux sondages soient incompatibles suggère que cela pourrait être le cas (ou au moins renforce le fait que les eaux sont boueuses).

Bien que deux soit une réponse parfaitement respectable, compatible avec la définition 4 ci-dessus et avec l’unilatéralité d’un cercle, je ne suis pas satisfait qu’elle soit définitivement la bonne, ou que trois ou quatre soient catégoriquement faux. Cela dépend de ce que vous voulez compter : les sections lisses, les bords droits, ou les bords droits plus ce qui reste, n’importe laquelle de ces réponses peut être la réponse que vous voulez selon le contexte (plus sur ce point ci-dessous). De même, je ne suis pas sûr que compter le nombre de sections lisses corresponde pleinement à mon intuition du mot « côté ». Après tout, les deux sections verticales de la pierre tombale sont – je pense qu’il est juste de dire – « sur des côtés opposés ». Sommes-nous vraiment satisfaits qu’elles fassent simultanément partie du « même côté » ?

Vous pourriez protester que je confonds deux significations différentes du mot « côté », que la terminologie s’entrechoque parfois, et que nous devons simplement vivre avec. Mais je n’en suis pas si sûr. Le but de cet exercice est d’extrapoler à partir d’une situation (figures rectilignes) où les deux notions s’accordent assez bien. S’il existait une nouvelle idée qui reprenait tout ce que nous aimions dans l’idée originale, mais qui s’appliquait également à une catégorie plus large de formes, alors cette idée aurait la prétention écrasante d’être l’unique bonne réponse. Mais si toutes nos tentatives de généralisation impliquent de sacrifier des aspects souhaitables de l’original, alors peut-être n’y a-t-il pas de généralisation correcte unique. Il y a différents choix, avec différents compromis, qui pourraient convenir dans différents contextes (et si nous sommes dans une situation où plus d’un sont en jeu, alors on pourrait utilement leur donner des noms différents).

Voici une autre variation : une pierre tombale de Weierstrass créée en remplaçant le bord supérieur d’un carré par une section de la fonction de Weiestress, une ligne infiniment ondulée qui n’est lisse nulle part.

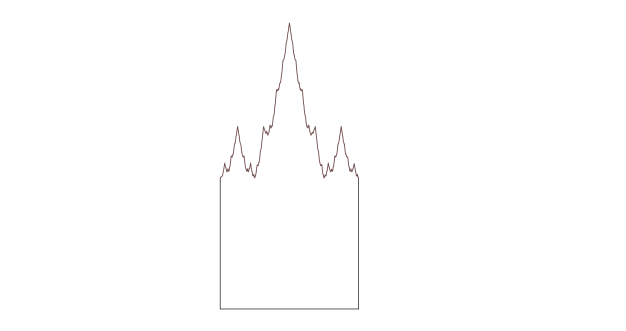
Voici (et remarquez la coquille) ce que mes amis Twitter en ont fait – bien que moins nombreux à se risquer à une opinion :

Malgré le scepticisme de mes followers Twitter, j’expliquerai dans une minute pourquoi je ne pense pas qu’il soit idiot de voir cela comme ayant quatre côtés (dont un non lisse). D’un autre côté, si vous préférez vos côtés lisses, alors vous avez à nouveau le choix entre voir qu’il a une infinité de côtés (dont trois ont la longueur 1, et le reste la longueur 0), ou avoir 3 côtés plus un tronçon de frontière définitivement pas un côté.

Pour un côté : une seule courbe lisse.
Contre un côté : le même côté sur des côtés opposés.

Sur une tangente 3 : côtés contre bords

Combien de côtés a un carré ? Quatre. Combien d’arêtes a-t-il ? Quatre. Alors, les arêtes et les côtés sont-ils la même chose ? Pas nécessairement. Voici deux configurations qui sont – au moins discutablement – chacune à quatre côtés mais qui ont respectivement 5 et 3 arêtes:

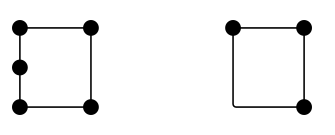
En général, je dirais qu’une « arête » est un objet topologique, en ce sens que c’est sa fonction, et non sa forme, qui importe. Pensez à la carte du métro de Londres. Si vous demandez combien d’arêtes il y a dans ce réseau, il n’y a aucun intérêt à additionner les sections droites ou lisses. Ce sont les connexions entre les stations (ou sommets) qui comptent.

Comme déjà mentionné, il est courant de penser à un polygone comme une sorte de réseau très simple appelé chaîne polygonale fermée : une chaîne de sommets (dans ce cas, les coins du polygone), reliés par des arêtes, de telle sorte que chaque sommet se trouve sur exactement deux arêtes, et que le tout forme une seule boucle. Dans cette situation, les arêtes et les côtés coïncident, tout comme les sommets et les coins. Mais en général, vous pouvez rompre cette concordance, comme dans les deux petits réseaux ci-dessus.

Si vous voulez penser aux choses de manière théorique en réseau, mais que les sommets ne sont pas clairement marqués, alors vous devez deviner où ils sont. Avec un polygone, c’est facile – les sommets sont aux coins – et c’est pourquoi le passage entre les approches géométriques et topologiques vient si naturellement. Mais avec d’autres formes, comme l’une ou l’autre des pierres tombales ci-dessus, cela peut ne pas être aussi évident. Néanmoins, dans chaque cas, si l’on vous dit qu’il y a des sommets quelque part et que l’on vous demande de les localiser, je pense qu’il serait raisonnable de supposer qu’il y en a quatre, à savoir les coins du carré original, et que le bord supérieur a, pour une raison ou une autre, été représenté comme une ligne non droite. Et si nous voulons penser les choses de cette façon, avec chacune des pierres tombales ayant 4 bords, alors cela pourrait sembler pervers (bien que logiquement cohérent !).) pour insister sur le fait qu’ils ont un autre nombre de côtés (d’autant plus que le côté supérieur est – malgré sa propre géométrie – clairement « sur un côté » de la figure). En fait, plutôt que de deviner, l’un de mes correspondants sur Twitter m’a demandé « Les deux sommets supérieurs ont-ils été supprimés ? », une question qui n’a de sens que du point de vue de la théorie des réseaux.

Où cela laisse-t-il le cercle ? Le problème est qu’aucun point du cercle n’a une meilleure prétention à être sommet qu’un autre. Donc, bien qu’il soit tentant (et encore une fois cohérent) de voir un cercle comme un réseau avec une arête, si nous allons insérer des sommets, il n’y a pas de raison évidente de préférer un seul à tout autre nombre.

Pourrait-on le voir comme un réseau sans sommets du tout, une sorte de ligne de métro sans stations ? La conception mathématique habituelle d’un réseau ne le permettrait pas, mais cela ne devrait pas trop nous décourager. Cela suggère une approche purement topologique. Le problème est que, de ce point de vue, si un cercle peut être une sorte de réseau sans sommets et avec une arête, il en va de même pour un carré (si c’est ainsi que la ligne de métro est disposée). En topologie, un carré est un cercle. (Ce n’est pas un paradoxe, il s’agit simplement de dire que la frontière est une boucle unique, dont la forme n’a pas d’importance). Ainsi, bien que ce type de réseau ait « une arête », il est évident qu’un carré n’a pas « un côté », de sorte que la relation entre les côtés (géométriques) et les arêtes (topologiques) est à nouveau rompue, tout comme dans les deux petits réseaux illustrés ci-dessus. Cette approche ne nous fait donc pas avancer très loin.

Pas de côtés ?

Il peut sembler paradoxal de soutenir qu’un cercle (ou toute forme) n’a « pas de côtés ». Mais l’argument en faveur de la défense est simple. Nous revenons à la définition 2 :

2. Ligne droite faisant partie de la limite d’une figure plane.

C’est une phrase simple, facilement compréhensible, qui rend parfaitement compte des côtés d’un carré. Nous n’avons pas réussi à trouver une généralisation satisfaisante de ceci aux figures courbes, donc la meilleure chose à faire est de s’en tenir à l’original. Et un cercle n’en a pas.

Pour aucun côté : vrai, selon une notion sensible de « côté ».
Contre aucun côté : ressemble à un koan zen.

None of the Above ?

Rappellez-vous la définition fournie par Google:

3. Chacune des lignes formant la limite d’une figure rectiligne plane.

Tenter d’appliquer cela à un cercle – une figure non rectiligne – ne produit rien. La question est aussi dénuée de sens que « Combien de côtés a le lundi ? »

Puisque la définition 3 est la plus officielle (la seule de ce billet qui n’a pas été inventée par moi ou mes enfants), cela ne fait-il pas de « Aucune des réponses ci-dessus » la bonne réponse catégorique ? Peut-être. D’un autre côté : lorsque quelqu’un nous pose une question, le principe de charité exige peut-être que nous supposions qu’elle est significative à moins que nous puissions fermement établir le contraire, et les définitions 1, 2, 4 et autres variantes rendent cela possible. En outre, la définition 3 est linguistique plutôt que formellement mathématique, et est donc descriptive plutôt que prescriptive, de sorte que nous ne devrions pas nous laisser enfermer par elle.

Pour rien de tout cela : dysfonctionnement sémantique.
Contre rien de tout cela : charité dialogique.

La bonne réponse

Qu’est-ce qui m’a poussé à écrire ce billet ? Comme d’innombrables élèves de l’école primaire, mes fils jumeaux de cinq ans – les élèves de l’école primaire mentionnés au début – se sont récemment vu poser cette question dans leurs devoirs. L’un a opté pour « 1 » et l’autre pour « 0 », et j’ai essayé de saisir et de développer leur raisonnement ci-dessus. Je pense que les deux réponses sont tout à fait défendables – et aucune n’est définitivement juste.

Alors, que faire si on vous pose la question : Combien de côtés a un cercle ? À mon avis, la réponse optimale est de demander au mathématicien de votre vie d’écrire un traité de 3000 mots sur le sujet, que vous pourrez ensuite imprimer et remettre triomphalement à votre malheureux professeur. Mais à défaut, la meilleure approche consiste à suivre l’exemple de Socrate et à répondre à la question par une contre-question : Qu’entendez-vous par « côté » ?

En fin de compte, compter jusqu’à zéro, ou jusqu’à un, ou refuser de répondre à la question, ne nous apprend pratiquement rien sur la géométrie des cercles. Mais il y a beaucoup à gagner en décortiquant les notions familières, en abandonnant ou en ajoutant des conditions supplémentaires, en défiant notre intuition en passant d’un contexte à un autre légèrement différent, et en essayant d’écrire précisément ce que nous entendons par un terme particulier dans un contexte particulier. C’est cela, les vraies mathématiques.

Notes de bas de page

Vous pourriez faire autre chose : par exemple, choisir un point de départ P sur le cercle, à partir duquel on mesure la distance autour de la circonférence. Puis déclarer que les points à distance rationnelle de P sont des coins et les autres des côtés. Cela a pour effet de produire un nombre infini de coins et un nombre infini de côtés. Ou bien on pourrait stipuler le contraire. Cela pourrait convenir à l’approche de la limite polygonale des cercles, mais j’aurais du mal à convenir que c’est assez facile ou évident pour être considéré comme « la bonne réponse ».

Un de mes correspondants sur Twitter s’inquiétait de la douceur de la courbe. Cette pierre tombale est continuellement différentiable mais pas deux fois. Il serait certainement intéressant que de nombreuses personnes pensent que c’est une question critique, et cela pourrait probablement être testé avec une pierre tombale infiniment lisse construite à partir de quelque chose comme cela, bien que je n’ai pas réfléchi aux détails.

Nous pourrions essayer de formaliser cela comme suit : dans un carré (ou tout polygone), un côté a la propriété que, en partant de n’importe quelle position à l’intérieur, vous pouvez couper la forme directement à travers votre emplacement, de sorte que votre côté choisi est fermement sur un côté de la coupe. Cela ne fonctionne pas pour la pierre tombale à deux côtés : toute coupe coupera toujours le côté long. Nous pourrions affaiblir cela en disant que pour compter comme un côté, il doit y avoir au moins un moyen de trancher la forme de sorte que le côté soit d’un côté de la coupe. Cela nous permettrait de dire que la pierre tombale a quatre côtés (même si la section incurvée ne se trouve pas sur un côté des points de la région supérieure). Pour le cercle par contre, son supposé un côté n’est jamais sur un côté (donc serait exclu), et seule la section droite d’un demi-cercle compterait comme un côté.

Il n’est pas facile de trouver une justification rigoureuse qui fonctionne pour les deux pierres tombales, mais je pense de manière plus informelle en termes de points de Schelling : c’est-à-dire des emplacements qui se distinguent comme étant spéciaux pour des raisons qui peuvent ne pas être faciles à prédire à l’avance.

Remerciements

Merciements à tous ceux qui ont participé ou retweeté mes sondages, ou discuté de cela avec moi sur Twitter.