Cinétique chimique
Cinétique chimique
Vous connaissez peut-être les titrages acide-base qui utilisent la phénolphtaléine comme indicateur de point final. Vous n’avez peut-être pas remarqué, cependant, ce qui se passe lorsqu’on laisse reposer pendant quelques minutes une solution qui contient de la phénolphtaléine en présence d’un excès de base. Bien que la solution ait initialement une couleur rose, elle devient progressivement incolore car la phénolphtaléine réagit avec l’ion OH- dans une solution fortement basique.
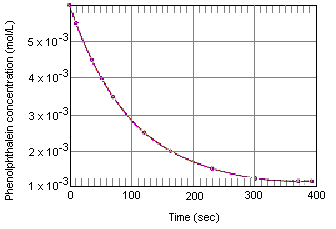
Le tableau ci-dessous montre ce qui arrive à la concentration de phénolphtaléine dans une solution qui était initialement 0,005 M en phénolphtaléine et 0,61 M en ion OH-. Comme vous pouvez le constater lorsque ces données sont reportées sur le graphique ci-dessous, la concentration en phénolphtaléine diminue d’un facteur 10 sur une période d’environ quatre minutes.
Données expérimentales de la réaction entre la phénolphtaléine et l’excès de base
Des expériences telles que celle qui nous a donné les données du tableau ci-dessus sont classées comme des mesures de cinétique chimique (d’une racine grecque signifiant » bouger « ). L’un des objectifs de ces expériences est de décrire la vitesse de réaction – la vitesse à laquelle les réactifs se transforment en produits de la réaction.
Le terme vitesse est souvent utilisé pour décrire le changement d’une quantité qui se produit par unité de temps. Le taux d’inflation, par exemple, est la variation du coût moyen d’une collection d’articles standard par an. La vitesse à laquelle un objet se déplace dans l’espace est la distance parcourue par unité de temps, comme les miles par heure ou les kilomètres par seconde. En cinétique chimique, la distance parcourue correspond à la variation de la concentration de l’un des composants de la réaction. La vitesse d’une réaction est donc le changement de la concentration d’un des réactifs![]() (X)
(X)![]() qui se produit pendant une période de temps donnée
qui se produit pendant une période de temps donnée![]() t.
t.
![]()
Problème pratique 1:
Utilisez les données du tableau ci-dessus pour calculer la vitesse à laquelle la phénolphtaléine réagit avec l’ion OH- pendant chacune des périodes suivantes:
(a) Pendant le premier intervalle de temps, lorsque la concentration de phénolphtaléine passe de 0,0050 M à 0,0045 M.
(b) Pendant le deuxième intervalle, lorsque la concentration tombe de 0,0045 M à 0,0040 M.
(c) Pendant le troisième intervalle, lorsque la concentration tombe de 0,0040 M à 0,0035 M.
Cliquez ici pour vérifier votre réponse au problème pratique 1.
Cliquez ici pour voir la solution du problème pratique 1.
![]()
Vitesses instantanées de réaction et loi de vitesse pour une réaction
La vitesse de la réaction entre la phénolphtaléine et l’ion OH n’est pas constante ; elle change avec le temps. Comme la plupart des réactions, la vitesse de cette réactiondiminue progressivement au fur et à mesure que les réactifs sont consommés. Cela signifie que la vitesse de la réactionchange pendant qu’elle est mesurée.
Pour minimiser l’erreur que cela introduit dans nos mesures, il semble conseillé de mesurer la vitesse de réaction sur des périodes de temps courtes par rapport au temps que met la réaction à se produire. Nous pouvons essayer, par exemple, de mesurer le changement infiniment petit de la concentration![]() d(X)
d(X)![]() qui se produit sur une période de temps infiniment courte. Le rapport de ces quantités est connu sous le nom de vitesse instantanée de réaction.
qui se produit sur une période de temps infiniment courte. Le rapport de ces quantités est connu sous le nom de vitesse instantanée de réaction.
![]()
La vitesse instantanée de réaction à tout moment peut être calculée à partir d’un graphique de la concentration du réactif (ou du produit) en fonction du temps. Le graphique ci-dessous montre comment la vitesse de réaction pour la décomposition de la phénolphtaléine peut être calculée à partir d’un graphique de la concentration en fonction du temps. La vitesse de réaction à tout moment dans le temps est égale à la pente d’une tangente tracée à cette courbe à ce moment.
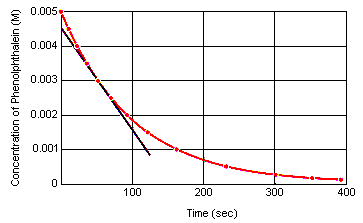
La vitesse instantanée de réaction peut être mesurée à tout moment entre l’instant où les réactifs sont mélangés et celui où la réaction atteint l’équilibre.En extrapolant ces données jusqu’à l’instant où les réactifs sont mélangés, on obtient la vitesse initialeinstantanée de réaction.
![]()
Lois de taux et constantes de taux
Un résultat intéressant est obtenu lorsque la vitesse instantanée de la réaction est calculée en divers points de la courbe du graphique de la section précédente. La vitesse de réaction à chaque point de cette courbe est directementproportionnelle à la concentration de phénolphtaléine à ce moment précis.
Vitesse = k(phénolphtaléine)
Parce que cette équation est une loi expérimentale qui décrit la vitesse de la réaction, on l’appelle la loi de vitesse de la réaction. La constante de proportionnalité, k, est connue comme la constante de vitesse.
Problème pratique 2:
Calculez la constante de vitesse de la réaction entre la phénolphtaléine et l’ion OH- si la vitesse instantanée de la réaction est de 2,5 x 10-5 mole par litre et par seconde lorsque la concentration de phénolphtaléine est de 0,0025 M.
Cliquez ici pour vérifier votre réponse au problème pratique 2.
Cliquez ici pour voir la solution du problème pratique 2.
Problème pratique 3:
Utilisez la constante de vitesse de la réaction entre la phénolphtaléine et l’ion OH- pour calculer la vitesse instantanée initiale de la réaction pour les données expérimentales énumérées dans le tableau précédent.
Cliquez ici pour vérifier votre réponse au problème pratique 3.
Cliquez ici pour voir une solution au problème pratique 3.
![]()
Différentes façons d’exprimer la vitesse de réaction
Il y a généralement plus d’une façon de mesurer la vitesse d’une réaction. Nous pouvons étudier la décomposition de l’iodure d’hydrogène, par exemple, en mesurant la vitesse à laquelle H2 ou I2 est formé dans la réaction suivante ou la vitesse à laquelle HI est consommé.
2 HI(g) H2(g) + I2(g)
Expérimentalement, nous trouvons que la vitesse à laquelle I2 est formé estproportionnelle au carré de la concentration de HI à tout moment dans le temps.
![]()
Que se passerait-il si nous étudiions la vitesse à laquelle H2 se forme ? L’équation équilibrée suggère que H2 et I2 doivent se former exactement à la même vitesse.
![]()
Que se passerait-il, cependant, si nous étudiions la vitesse à laquelle HI est consommé dans cette réaction ? Parce que HI est consommé, le changement de sa concentration doit être un nombre négatif. Par convention, la vitesse d’une réaction est toujours exprimée par un nombre positif. Nous devons donc changer le signe avant de rapporter le taux de réaction pour un agent qui est consommé dans la réaction.
![]()
Le signe négatif fait deux choses. Mathématiquement, il convertit un changement négatif de la concentration de HI en un taux positif. Physiquement, il nous rappelle que laconcentration du réactif diminue avec le temps.
Quel est le rapport entre le taux de réaction obtenu en surveillant la formation de H2 ou de I2 et le taux obtenu en observant la disparition de HI ? La stoechiométrie de la réaction indique que deux molécules de HI sont consommées pour chaque molécule de H2 ou I2 produite. Cela signifie que la vitesse de décomposition de HI est deux fois plus rapide que la vitesse à laquelle H2 et I2 sont formés. Nous pouvons traduire cette relation en une équation mathématique comme suit.
![]()
En conséquence, la constante de vitesse obtenue en étudiant la vitesse à laquelle H2 et I2 sont formés dans cette réaction (k) n’est pas la même que la constante de vitesse obtenue en surveillant la vitesse à laquelle HI est consommé (k’)
Problème pratique 4:
Calculez la vitesse à laquelle HI disparaît dans la réaction suivante au moment où I2 est formé à un taux de 1.8 x 10-6 moles par litre et par seconde:
2 HI(g) ![]() H2(g) + I2(g)
H2(g) + I2(g)
Cliquez ici pour vérifier votre réponse au problème pratique 4.
Cliquez ici pour voir une solution au problème pratique 4.
![]()
La loi de vitesse versus la stœchiométrie d’une réaction
Dans les années 1930, Sir Christopher Ingold et ses collègues de l’Université deLondres ont étudié la cinétique des réactions de substitution telles que les suivantes .
CH3Br(aq) + OH-(aq)
CH3OH(aq) + Br-(aq)
Ils ont constaté que la vitesse de cette réaction est proportionnelle auxconcentrations des deux réactifs.
Rapidité = k(CH3Br)(OH-)
Lorsqu’ils ont effectué une réaction similaire sur un matériau de départ légèrement différent, ils ont obtenu des produits similaires.
(CH3)3CBr(aq) + OH-(aq)![]() (CH3)3COH(aq) + Br-(aq)
(CH3)3COH(aq) + Br-(aq)
Mais maintenant la vitesse de réaction était proportionnelle à la concentration d’un seul des réactifs.
Rate = k((CH3)3CBr)
Ces résultats illustrent un point important : La loi de vitesse d’une action ne peut pas être prédite à partir de la stœchiométrie de la réaction ; elle doit être déterminéeexpérimentalement. Parfois, la loi de vitesse est cohérente avec ce que nous attendons de la stœchiométrie de la réaction.
2 HI(g) H2(g) + I2(g)
Rate = k(HI)2
Souvent, cependant, ce n’est pas le cas.
| 2 N2O5(g) |
Rapidité = k(N2O5) |
![]()
Ordre de la molécularité
Certaines réactions se produisent en une seule étape. La réaction dans laquelle un atome de chlore est transféré de ClNO2 à NO pour former NO2 et ClNO est un bon exemple de réaction à une étape.
ClNO2(g) + NO(g)
NO2(g) + ClNO(g)
D’autres réactions se produisent par une série d’étapes individuelles. N2O5,par exemple, se décompose en NO2 et O2 par un mécanisme en trois étapes.
| Etape 1 : | N2O5 |
|
| Etape 2 : | NO2 + NO3 |
|
| Etape 3 : | NO + NO3 |
Les étapes d’une réaction sont classées en termes de molécularité, qui décrit le nombre de molécules consommées. Lorsqu’une seule molécule est consommée, l’étape est dite unimoléculaire. Lorsque deux molécules sontconsommées, elle est bimoléculaire.
Problème pratique 5:
Déterminez la molécularité de chaque étape de la réaction par laquelle N2O5 se décompose en NO2 et O2.
Cliquez ici pour vérifier votre réponse au problème pratique 5.
Cliquez ici pour voir une solution au problème pratique 5.
Les réactions peuvent également être classées en fonction de leur ordre. La décomposition de N2O5 est une réaction de premier ordre car le taux de réaction dépend de la concentration de N2O5 élevée à la première puissance.
Rate = k(N2O5)
La décomposition de HI est une réaction de second ordre car le taux de réaction dépend de la concentration de HI élevée à la seconde puissance.
Rate = k(HI)2
Lorsque la vitesse d’une réaction dépend de plus d’un réactif, on classe la réaction en fonction de l’ordre de chaque réactif.
Problème pratique 6:
Classez l’ordre de la réaction entre NO et O2 pour former NO2:
2 NO(g) + O2(g) ![]() 2 NO2(g)
2 NO2(g)
Supposez la loi de vitesse suivante pour cette réaction:
Rate = k(NO)2(O2)
Cliquez ici pour vérifier votre réponse au problème pratique 6.
La différence entre la molécularité et l’ordre d’une réaction est importante. La molécularité d’une réaction, ou une étape dans une réaction,décrit ce qui se passe au niveau moléculaire. L’ordre d’une réaction décrit ce qui se passe à l’échelle macroscopique. Nous déterminons l’ordre d’une réaction en observant l’apparition des produits de la réaction ou la disparition des réactifs. Le caractère moléculaire de la réaction est quelque chose que nous déduisons pour expliquer ces résultats expérimentaux.
![]()
Modèle de la théorie des collisions des réactions chimiques
Le modèle de la théorie des collisions des réactions chimiques peut être utilisé pour expliquer les lois de vitesse observées pour les réactions à une étape et à plusieurs étapes. Ce modèle suppose que la vitesse de toute étape d’une réaction dépend de la fréquence des collisions entre les particules impliquées dans cette étape.
La figure ci-dessous fournit une base pour comprendre les implications du modèle de la théorie des collisions pour des réactions simples, à une étape, telles que les suivantes.
ClNO2(g) + NO(g) ![]() NO2(g) + ClNO(g)
NO2(g) + ClNO(g)
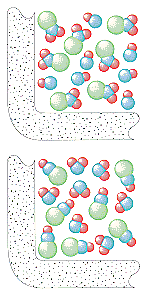
La théorie cinétique moléculaire suppose que le nombre de collisions par seconde dans un gaz dépend du nombre de particules par litre. La vitesse à laquelle NO2et ClNO sont formés dans cette réaction devrait donc être directement proportionnelle auxconcentrations de ClNO2 et de NO.
Rate = k(ClNO2)(NO)
Le modèle de la théorie des collisions suggère que la vitesse de toute étape d’une action est proportionnelle aux concentrations des réactifs consommés dans cette étape. La loi du taux pour une réaction à une étape devrait donc correspondre à la stœchiométrie de cette réaction.
La réaction suivante, par exemple, se produit en une seule étape.
CH3Br(aq) + OH-(aq) ![]() CH3OH(aq) + Br-(aq)
CH3OH(aq) + Br-(aq)
Lorsque ces molécules entrent en collision dans la bonne orientation, une paire d’électrons non liants sur l’ion OH- peut être donnée à l’atome de carbone au centre de la molécule de CH3Br, comme le montre la figure ci-dessous.
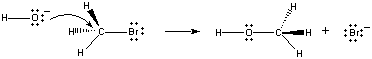
Lorsque cela se produit, une liaison carbone-oxygène se forme en même temps que la liaison carbone-brome est rompue. Le résultat net de cette réaction est la substitution d’un ion OH- par un ion Br -. Parce que la réaction se produit en une seule étape, qui implique des collisions entre les deux réactifs, la vitesse de cette réaction estproportionnelle à la concentration des deux réactifs.
Vitesse = k(CH3Br)(OH-)
Les réactions ne se produisent pas toutes en une seule étape. La réaction suivante se produit en trois étapes, comme le montre la figure ci-dessous.
(CH3)3CBr(aq) + OH-(aq)![]() (CH3)3COH(aq) + Br-(aq)
(CH3)3COH(aq) + Br-(aq)
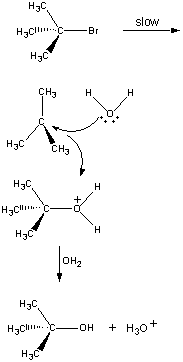
Dans la première étape, la molécule de (CH3)3CBr dissocie en une paire d’ions.
| Première étape | 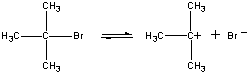 |
L’ion (CH3)3C+ chargé positivement réagit ensuite avec l’eau dans une deuxième étape.
| Deuxième étape | 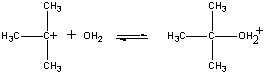 |
Le produit de cette réaction perd ensuite un proton soit à l’ion OH, soit à l’eau dans la dernière étape.
| Troisième étape | 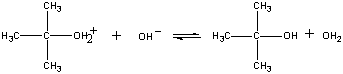 |
Les deuxième et troisième étapes de cette réaction sont beaucoup plus rapides que la première.
| (CH3)3CBr |
Étape lente | |
| (CH3)3C+ + H2O |
Étape rapide | |
| (CH3)3COH2+ + OH- |
Étape rapide |
La vitesse globale de la réaction est donc plus ou moins égale à la vitesse de la première étape. La première étape est donc appelée l’étape limitant la vitesse de cette réaction car elle limite littéralement la vitesse à laquelle les produits de la réaction peuvent être formés. Comme un seul réactif est impliqué dans l’étape limitant la vitesse, la vitesse globale de la réaction est proportionnelle à la concentration de ce seul réactif.
Vitesse = k((CH3)3CBr)
La loi de vitesse de cette réaction diffère donc de ce que nous pourrions prédire à partir de la stœchiométrie de la réaction. Bien que la réaction consomme à la fois (CH3)3CBr et OH-, la vitesse de la réaction est seulement proportionnelle à la concentration de(CH3)3CBr.
Les lois de vitesse des réactions chimiques peuvent être expliquées par les règles générales suivantes.
La vitesse de toute étape d’une réaction est directement proportionnelle aux concentrations des réactifs consommés dans cette étape.
La loi de vitesse globale d’une réaction est déterminée par la séquence d’étapes, ou le mécanisme, par lequel les réactifs sont convertis en produits de la réaction.
La loi de vitesse globale d’une réaction est dominée par la loi de vitesse de l’étape la plus lente de la réaction.
.