Classification par analyse discriminante
Voyons comment LDA peut être dérivée comme méthode de classification supervisée. Considérons un problème de classification générique : une variable aléatoire X provient d’une des K classes, avec certaines densités de probabilité f(x) spécifiques aux classes. Une règle discriminante tente de diviser l’espace de données en K régions disjointes qui représentent toutes les classes (imaginez les cases d’un échiquier). Avec ces régions, la classification par analyse discriminante signifie simplement que nous attribuons x à la classe j si x se trouve dans la région j. La question est alors de savoir comment savoir dans quelle région se trouve la donnée x ? Naturellement, Nous pouvons suivre deux règles d’attribution :
- Règle du maximum de vraisemblance : Si nous supposons que chaque classe pourrait se produire avec une probabilité égale, alors attribuez x à la classe j si

- Règle bayésienne : Si nous connaissons les probabilités antérieures des classes, π, alors allouez x à la classe j si

Analyse discriminante linéaire et quadratique
Si nous supposons que les données proviennent d’une distribution gaussienne multivariée, c’est-à-dire.c’est-à-dire que la distribution de X peut être caractérisée par sa moyenne (μ) et sa covariance (Σ), on peut obtenir des formes explicites des règles de répartition ci-dessus. En suivant la règle bayésienne, on classe la donnée x dans la classe j si elle a la plus grande vraisemblance parmi toutes les K classes pour i = 1,…,K:

La fonction ci-dessus est appelée fonction discriminante. Notez l’utilisation de la log-vraisemblance ici. En d’autres termes, la fonction discriminante nous indique la probabilité que les données x appartiennent à chaque classe. La frontière de décision séparant deux classes, k et l, est donc l’ensemble des x pour lesquels deux fonctions discriminantes ont la même valeur. Par conséquent, toute donnée qui tombe sur la frontière de décision est également probable à partir des deux classes (nous ne pouvions pas décider).
LDA se présente dans le cas où nous supposons une covariance égale entre K classes. C’est-à-dire qu’au lieu d’une matrice de covariance par classe, toutes les classes ont la même matrice de covariance. Nous pouvons alors obtenir la fonction discriminante suivante :

Notez que c’est une fonction linéaire en x. Ainsi, la frontière de décision entre toute paire de classes est également une fonction linéaire en x, d’où son nom : analyse discriminante linéaire. Sans l’hypothèse de covariance égale, le terme quadratique dans la vraisemblance ne s’annule pas, donc la fonction discriminante résultante est une fonction quadratique en x :

Dans ce cas, la frontière de décision est quadratique en x. C’est ce qu’on appelle l’analyse discriminante quadratique (QDA).
Quel est le meilleur ? LDA ou QDA?
Dans les problèmes réels, les paramètres de population sont généralement inconnus et estimés à partir des données d’entraînement comme les moyennes d’échantillon et les matrices de covariance d’échantillon. Bien que QDA s’adapte à des frontières de décision plus flexibles par rapport à LDA, le nombre de paramètres nécessaires à l’estimation augmente également plus rapidement que celui de LDA. Pour LDA, (p+1) paramètres sont nécessaires pour construire la fonction discriminante dans (2). Pour un problème avec K classes, nous n’aurions besoin que de (K-1) fonctions discriminantes en choisissant arbitrairement une classe comme classe de base (en soustrayant la vraisemblance de la classe de base de toutes les autres classes). Par conséquent, le nombre total de paramètres estimés pour LDA est (K-1)(p+1).
D’autre part, pour chaque fonction discriminante QDA dans (3), le vecteur moyen, la matrice de covariance et la priorité de classe doivent être estimés :
– Moyenne : p
– Covariance : p(p+1)/2
– Priorité de classe : 1
De même, pour QDA, nous devons estimer (K-1){p(p+3)/2+1} paramètres.
Par conséquent, le nombre de paramètres estimés dans LDA augmente linéairement avec p alors que celui de QDA augmente quadratiquement avec p. Nous nous attendrions à ce que QDA ait de moins bonnes performances que LDA lorsque la dimension du problème est grande.
Le meilleur des deux mondes ? Compromis entre LDA & QDA
Nous pouvons trouver un compromis entre LDA et QDA en régularisant les matrices de covariance des classes individuelles. La régularisation signifie que nous mettons une certaine restriction sur les paramètres estimés. Dans ce cas, nous exigeons que la matrice de covariance individuelle se rétrécisse vers une matrice de covariance commune mise en commun par un paramètre de pénalité, par exemple, α:

La matrice de covariance commune peut également être régularisée vers une matrice d’identité par un paramètre de pénalité, par exemple, β:

Dans les situations où le nombre de variables d’entrée dépasse largement le nombre d’échantillons, la matrice de covariance peut être mal estimée. Le rétrécissement peut, on l’espère, améliorer l’estimation et la précision de la classification. Ceci est illustré par la figure ci-dessous.

Calcul pour LDA
Nous pouvons voir à partir de (2) et (3) que les calculs des fonctions discriminantes peuvent être simplifiés si nous diagonalisons les matrices de covariance en premier. C’est-à-dire que les données sont transformées pour avoir une matrice de covariance identité (pas de corrélation, variance de 1). Dans le cas de LDA, voici comment nous procédons au calcul :

L’étape 2 sphérique les données pour produire une matrice de covariance identité dans l’espace transformé. L’étape 4 est obtenue en suivant (2).
Prenons un exemple à deux classes pour voir ce que fait réellement LDA. Supposons qu’il existe deux classes, k et l. Nous classons x dans la classe k si

La condition ci-dessus signifie que la classe k est plus susceptible de produire la donnée x que la classe l. En suivant les quatre étapes décrites ci-dessus, nous écrivons
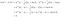
C’est-à-dire, nous classons les données x dans la classe k si

La règle d’allocation dérivée révèle le fonctionnement de LDA. Le côté gauche (l.h.s.) de l’équation est la longueur de la projection orthogonale de x* sur le segment de droite joignant les deux moyennes de classe. Le côté droit est l’emplacement du centre du segment corrigé par les probabilités antérieures de la classe. Essentiellement, LDA classe les données sphériques à la moyenne de classe la plus proche. Nous pouvons faire deux observations ici :
- Le point de décision s’écarte du point central lorsque les probabilités préalables de classe ne sont pas les mêmes, c’est-à-dire que la limite est repoussée vers la classe dont la probabilité préalable est la plus faible.
- Les données sont projetées sur l’espace couvert par les moyennes de classe (la multiplication de x* et la soustraction de la moyenne sur l’axe des l.h.s. de la règle). Les comparaisons de distance sont ensuite effectuées dans cet espace.