Équation de continuité Écoulement des fluides – Engineers Edge

L’équation de continuité est simplement une expression mathématique du principe de conservation de la masse. Pour un volume de contrôle qui a une seule entrée et une seule sortie, le principe de conservation de la masse stipule que, pour un écoulement en régime permanent, le débit massique entrant dans le volume doit être égal au débit massique sortant. L’équation de continuité pour cette situation est exprimée par l’équation 3-5.

Pour un volume de contrôle avec plusieurs entrées et sorties, le principe de conservation de la masse exige que la somme des débits massiques dans le volume de contrôle soit égale à la somme des débits massiques hors du volume de contrôle. L’équation de continuité pour cette situation plus générale est exprimée par l’équation 3-6.

L’une des applications les plus simples de l’équation de continuité consiste à déterminer le changement de vitesse du fluide dû à une expansion ou à une contraction du diamètre d’un tuyau.

Exemple : Équation de continuité – Expansion de la tuyauterie

Un écoulement en état d’équilibre existe dans une tuyauterie qui subit une expansion graduelle d’un diamètre de 6 po à un diamètre de 8 po. La densité du fluide dans le tuyau est constante à 60,8 lbm/ft3. Si la vitesse d’écoulement est de 22,4 pi/sec dans la section de 6 po, quelle est la vitesse d’écoulement dans la section de 8 po ?

Solution:

D’après l’équation de continuité, nous savons que le débit massique dans la section de 6 po doit être égal au débit massique dans la section de 8 po. En laissant l’indice 1 représenter la section de 6 pouces et 2 représenter la section de 8 pouces, nous avons ce qui suit.

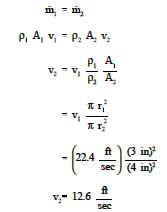
Donc, en utilisant l’équation de continuité, nous trouvons que l’augmentation du diamètre du tuyau de 6 à 8 pouces a causé une diminution de la vitesse d’écoulement de 22.4 à 12,6 pi/sec.

L’équation de continuité peut également être utilisée pour montrer qu’une diminution du diamètre du tuyau entraîne une augmentation de la vitesse d’écoulement.

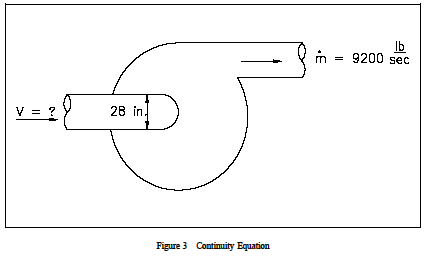
Exemple : Équation de continuité – pompe centrifuge Le diamètre d’entrée de la pompe de refroidissement du réacteur illustrée à la figure 3 est de 28 po, tandis que le débit de sortie à travers la pompe est de 9200 lbm/sec. La densité de l’eau est de 49 lbm/ft3. Quelle est la vitesse à l’entrée de la pompe ?

L’exemple ci-dessus indique que le débit entrant dans le système est le même que celui sortant du système. Le même concept est vrai même si plus d’une voie d’écoulement peut entrer ou sortir du système en même temps. Le bilan massique est simplement ajusté pour indiquer que la somme de tous les flux entrant dans le système est égale à la somme de tous les flux sortant du système si les conditions d’équilibre existent. Un exemple de ce cas physique est inclus dans l’exemple suivant.

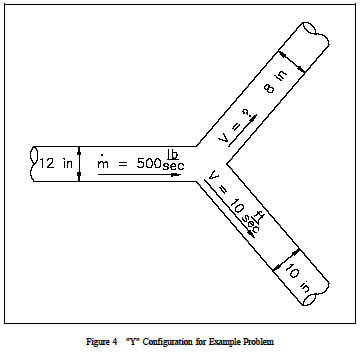
Exemple : Équation de continuité – Sorties multiples

Un système de tuyauterie présente une configuration en « Y » pour séparer l’écoulement, comme le montre la figure 4. Le diamètre de la branche d’entrée est de 12 po, et les diamètres des branches de sortie sont de 8 et 10 po. La vitesse dans la branche de 10 pouces est de 10 pieds/seconde. Le débit dans la partie principale est de 500 lbm/sec. La densité de l’eau est de 62,4 lbm/ft3. Quelle est la vitesse à la sortie de la section de tuyau de 8 po?

.
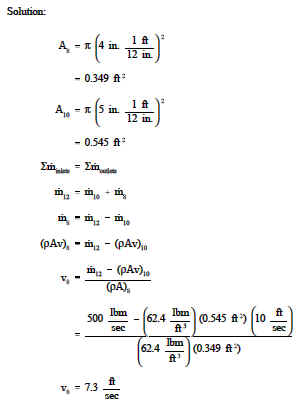