- Learning Outcomes
- Lineares (algebraisches) Wachstum
- Wachstum vorhersagen
- Lineares Wachstum
- Rekursive Form
- Explizite Form
- Verbindung zum vorherigen Lernen: Steigung und Achsenabschnitt
- Beispiele
- Rekursive Form
- Explizite Form
- Rekursive Form
- Explizite Form
- Versuchen Sie es
- Wenn gute Modelle schlecht werden
- Beispiel
- Rekursive Form
- Explizite Form
- Exponentielles (geometrisches) Wachstum
- Populationswachstum
- Exponentielles Wachstum
- Rekursive Form
- Explizite Form
- Beispiel
- Auswerten von Exponenten auf dem Taschenrechner
- Versuchen Sie es
- Beispiele
- Rundung
- Wurzeln mit dem Taschenrechner auswerten
- Versuchen Sie es
- Beispiel
Learning Outcomes
- Bestimmen, ob Daten oder ein Szenario lineares oder geometrisches Wachstum beschreiben
- Erkennen Sie Wachstumsraten, Anfangswerte oder Punktwerte, die verbal, grafisch oder numerisch ausgedrückt werden, oder numerisch ausgedrückt werden, und übersetzen sie in ein Format, das für Berechnungen verwendet werden kann
- Berechnen Sie rekursive und explizite Gleichungen für lineares und geometrisches Wachstum, wenn genügend Informationen vorliegen, und verwenden Sie diese Gleichungen, um Vorhersagen zu treffen
Eine konstante Änderungsrate ist das bestimmende Merkmal des linearen Wachstums. Die Darstellung von Koordinatenpaaren, die mit einer konstanten Veränderung verbunden sind, ergibt eine gerade Linie, die Form des linearen Wachstums. In diesem Abschnitt werden wir eine Methode zur Beschreibung des linearen Wachstums mit Hilfe mathematischer Begriffe und Konzepte formalisieren. Am Ende dieses Abschnitts werden Sie in der Lage sein, sowohl eine rekursive als auch eine explizite Gleichung für lineares Wachstum bei gegebenen Ausgangsbedingungen oder einer Änderungskonstante zu schreiben. Sie werden auch in der Lage sein, den Unterschied zwischen linearem und geometrischem Wachstum anhand eines Graphen oder einer Gleichung zu erkennen.

Lineares (algebraisches) Wachstum
Wachstum vorhersagen
Marco ist ein Sammler von antiken Limonadenflaschen. Seine Sammlung umfasst derzeit 437 Flaschen. Jedes Jahr budgetiert er genug Geld, um 32 neue Flaschen zu kaufen. Können wir bestimmen, wie viele Flaschen er in 5 Jahren haben wird und wie lange es dauert, bis seine Sammlung 1000 Flaschen erreicht?

Während man diese beiden Fragen wahrscheinlich auch ohne Gleichung oder formale Mathematik lösen könnte, werden wir unsere Herangehensweise an dieses Problem formalisieren, um ein Mittel zur Beantwortung komplizierterer Fragen zur Verfügung zu stellen.
Angenommen, dass Pn die Anzahl oder Population der Flaschen darstellt, die Marco nach n Jahren hat. Also würde P0 die Anzahl der Flaschen jetzt darstellen, P1 die Anzahl der Flaschen nach 1 Jahr, P2 die Anzahl der Flaschen nach 2 Jahren usw. Wir könnten die Entwicklung von Marcos Flaschensammlung folgendermaßen beschreiben:
P0 = 437
Pn = Pn-1 + 32
Dies nennt man eine rekursive Beziehung. Eine rekursive Beziehung ist eine Formel, die den nächsten Wert in einer Folge mit den vorherigen Werten in Beziehung setzt. In diesem Fall kann die Anzahl der Flaschen im Jahr n ermittelt werden, indem man 32 zur Anzahl der Flaschen im vorherigen Jahr, Pn-1, addiert. Mit dieser Beziehung können wir berechnen:
P1 = P0 + 32 = 437 + 32 = 469
P2 = P1 + 32 = 469 + 32 = 501
P3 = P2 + 32 = 501 + 32 = 533
P4 = P3 + 32 = 533 + 32 = 565
P5 = P4 + 32 = 565 + 32 = 597
Wir haben die Frage beantwortet, wie viele Flaschen Marco in 5 Jahren haben wird. 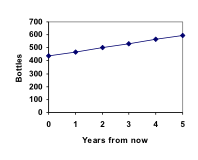
Die Lösung der Frage, wie lange es dauert, bis seine Sammlung 1000 Flaschen erreicht hat, würde jedoch viel mehr Berechnungen erfordern.
Während rekursive Beziehungen hervorragend geeignet sind, um einfach und sauber zu beschreiben, wie sich eine Menge verändert, sind sie nicht geeignet, um Vorhersagen zu machen oder Probleme zu lösen, die weit in die Zukunft reichen. In diesem Fall ist eine geschlossene oder explizite Form für die Beziehung vorzuziehen. Eine explizite Gleichung ermöglicht es uns, Pn direkt zu berechnen, ohne dass wir Pn-1 kennen müssen. Obwohl Sie die explizite Gleichung vielleicht schon erraten können, wollen wir sie aus der rekursiven Formel ableiten. Wir können dies tun, indem wir selektiv nicht vereinfachen:
P1 = 437 + 32 = 437 + 1(32)
P2 = P1 + 32 = 437 + 32 + 32 = 437 + 2(32)
P3 = P2 + 32 = (437 + 2(32)) + 32 = 437 + 3(32)
P4 = P3 + 32 = (437 + 3(32)) + 32 = 437 + 4(32)
Du kannst jetzt wahrscheinlich das Muster erkennen und verallgemeinern, dass
Pn = 437 + n(32) = 437 + 32n
Mit dieser Gleichung können wir berechnen, wie viele Flaschen er nach 5 Jahren haben wird:
P5 = 437 + 32(5) = 437 + 160 = 597
Wir können nun auch berechnen, wann die Sammlung 1000 Flaschen erreichen wird, indem wir 1000 für Pn einsetzen und n
1000 = 437 + 32n
563 = 32n
n = 563/32 = 17.59
Marco wird also in 18 Jahren 1000 Flaschen erreichen.
Die Schritte zur Bestimmung der Formel und zur Lösung des Problems von Marcos Flaschensammlung werden in den folgenden Videos ausführlich erklärt.
In diesem Beispiel ist Marcos Sammlung jedes Jahr um die gleiche Anzahl von Flaschen gewachsen. Diese konstante Veränderung ist das entscheidende Merkmal des linearen Wachstums. Wenn wir die Werte, die wir für Marcos Sammlung berechnet haben, auftragen, sehen wir, dass die Werte eine gerade Linie bilden, die Form des linearen Wachstums.
Lineares Wachstum
Wenn eine Menge bei der Größe P0 beginnt und in jeder Zeitperiode um d wächst, dann kann die Menge nach n Zeitperioden mit einer der beiden folgenden Beziehungen bestimmt werden:
Rekursive Form
Pn = Pn-1 + d
Explizite Form
Pn = P0 + d n
In dieser Gleichung stellt d die gemeinsame Differenz dar – den Betrag, um den sich die Population jedes Mal ändert, wenn n um 1 wächst.
Verbindung zum vorherigen Lernen: Steigung und Achsenabschnitt
Die gemeinsame Differenz d in unserer linearen Gleichung erkennen Sie vielleicht als Steigung. Tatsächlich sollte Ihnen die gesamte Gleichung bekannt vorkommen – es ist dieselbe lineare Gleichung, die Sie in Algebra gelernt haben, wahrscheinlich als y = mx + b.
In der algebraischen Standardgleichung y = mx + b war b der y-Achsenabschnitt oder der y-Wert, wenn x Null war. In der von uns verwendeten Form der Gleichung verwenden wir P0, um diesen Anfangsbetrag darzustellen.
In der Gleichung y = mx + b ist m die Steigung. In jedem Fall stellt sie dasselbe dar wie die von uns verwendete gemeinsame Differenz d – den Betrag, um den sich der Ausgang Pn ändert, wenn sich der Eingang n um 1 erhöht.
Die Gleichungen y = mx + b und Pn = P0 + d n bedeuten dasselbe und können auf dieselbe Weise verwendet werden. Wir schreiben sie nur etwas anders.
Beispiele
Die Elchpopulation in einem Nationalwald wurde 2003 mit 12.000 Tieren gemessen und 2007 mit 15.000. Wenn die Population weiterhin linear mit dieser Rate wächst, wie hoch wird dann die Elchpopulation im Jahr 2014 sein?
Weitere Informationen zu diesem Beispiel finden Sie hier.
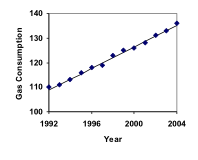
Der Benzinverbrauch in den USA ist stetig gestiegen. Nachstehend sind die Verbrauchsdaten von 1992 bis 2004 aufgeführt. Finden Sie ein Modell für diese Daten, und verwenden Sie es, um den Verbrauch im Jahr 2016 vorherzusagen. Wenn der Trend anhält, wann wird der Verbrauch 200 Milliarden Gallonen erreichen?
| Jahr | ’92 | ’93 | ’94 | ’95 | ’96 | ’97 | ’98 | ’99 | ’00 | ’01 | ’02 | ’03 | ’04 |
| Verbrauch (Milliarden von Gallonen) | 110 | 111 | 113 | 116 | 118 | 119 | 123 | 125 | 126 | 128 | 131 | 133 | 136 |
Die Schritte, um zu dieser Antwort zu gelangen, sind im folgenden Video ausführlich dargestellt.
Die Kosten in Dollar für eine Mitgliedschaft im Fitnessstudio für n Monate können durch die explizite Gleichung Pn = 70 + 30n beschrieben werden. Was sagt uns diese Gleichung?
Die Erklärung für dieses Beispiel wird weiter unten gegeben.
Versuchen Sie es
Die Zahl der Väter, die zu Hause bleiben, ist in Kanada stetig gestiegen. Der Trend ist zwar nicht vollkommen linear, aber doch ziemlich gleichmäßig. Verwenden Sie die Daten aus den Jahren 1976 und 2010, um eine eindeutige Formel für die Anzahl der Väter zu finden, die zu Hause bleiben, und verwenden Sie diese, um die Anzahl im Jahr 2020 vorherzusagen.
| Jahr | 1976 | 1984 | 1991 | 2000 | 2010 |
| # der Stay -at-Heimväter | 20610 | 28725 | 43530 | 47665 | 53555 |
Wenn gute Modelle schlecht werden
Bei der Verwendung mathematischer Modelle zur Vorhersage zukünftigen Verhaltens ist es wichtig zu bedenken, dass nur sehr wenige Trends auf unbestimmte Zeit anhalten werden.
Beispiel
Angenommen, ein vierjähriger Junge ist derzeit 39 cm groß, und man sagt ihm, dass er pro Jahr 2,5 cm wachsen wird.
Wir können ein Wachstumsmodell aufstellen, wobei n = 0 dem Alter von 4 Jahren entspricht.
Rekursive Form
P0 = 39
Pn = Pn-1 + 2.5
Explizite Form
Pn = 39 + 2.5(n)
Im Alter von 6 Jahren würden wir also erwarten, dass er
P2 = 39 + 2.5(2) = 44 Zoll groß ist
Jedes mathematische Modell wird irgendwann zusammenbrechen. Sicherlich sollten wir nicht erwarten, dass dieser Junge sein ganzes Leben lang mit der gleichen Geschwindigkeit wächst. Wenn er das täte, wäre er im Alter von 50 Jahren
P46 = 39 + 2,5(46) = 154 Zoll groß = 12,8 Fuß groß!
Wenn wir ein mathematisches Modell verwenden, müssen wir überlegen, welche Eingaben sinnvoll sind. Wann immer wir extrapolieren oder Vorhersagen für die Zukunft treffen, gehen wir davon aus, dass das Modell weiterhin gültig ist.
Schauen Sie sich hier ein Erklärungsvideo zu dieser Aufschlüsselung des linearen Wachstumsmodells an.
Exponentielles (geometrisches) Wachstum
Populationswachstum
Angenommen, dass jedes Jahr nur 10% der Fische in einem See überlebende Nachkommen haben. Wenn im letzten Jahr 100 Fische im See waren, wären es jetzt 110 Fische. Wenn im letzten Jahr 1000 Fische im See waren, wären es jetzt 1100 Fische. Wenn es keine hemmenden Faktoren gibt, neigen Populationen von Menschen und Tieren dazu, jedes Jahr um einen Prozentsatz der bestehenden Population zu wachsen.

Angenommen, unser See begann mit 1000 Fischen, und 10 % der Fische haben jedes Jahr überlebende Nachkommen. Da wir mit 1000 Fischen beginnen, ist P0 = 1000. Wie berechnen wir P1? Die neue Population ist die alte Population plus zusätzliche 10%. Symbolisch:
P1 = P0 + 0,10P0
Dies kann durch Faktorisierung auf eine kürzere Form gebracht werden:
P1 = P0 + 0,10P0 = 1P0 + 0,10P0 = (1+ 0,10)P0 = 1,10P0
Während 10% die Wachstumsrate ist, ist 1,10 der Wachstumsmultiplikator. Beachten Sie, dass man sich 1,10 als „die ursprünglichen 100 % plus zusätzliche 10 %“ vorstellen kann.
Für unsere Fischpopulation
P1 = 1,10(1000) = 1100
Wir könnten dann die Population in späteren Jahren berechnen:
P2 = 1,10P1 = 1,10(1100) = 1210
P3 = 1,10P2 = 1,10(1210) = 1331
Beachte, dass im ersten Jahr die Population um 100 Fische wuchs; im zweiten Jahr wuchs die Population um 110 Fische; und im dritten Jahr wuchs die Population um 121 Fische.
Während der prozentuale Zuwachs konstant ist, nimmt die tatsächliche Zunahme der Anzahl der Fische jedes Jahr zu.
Wenn wir diese Werte grafisch darstellen, sehen wir, dass dieses Wachstum nicht ganz linear verläuft.
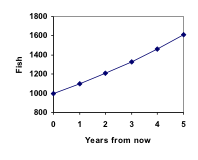
Ein Überblick über dieses Fischszenario kann hier eingesehen werden:
Um ein besseres Bild davon zu bekommen, wie sich dieses prozentuale Wachstum auswirkt, brauchen wir eine explizite Form, damit wir schnell Werte in der Zukunft berechnen können.
Wie beim linearen Modell gehen wir von der rekursiven Gleichung aus:
P1 = 1,10(P0 )= 1,10(1000)
P2 = 1,10(P1 )= 1,10(1,10(1000)) = 1,102(1000)
P3 = 1.10(P2 )= 1.10(1.102(1000)) = 1.103(1000)
P4 = 1.10(P3 )= 1.10(1.103(1000)) = 1.104(1000)
Beim Beobachten eines Musters können wir die explizite Form verallgemeinern zu:
Pn = 1.10n(1000), oder äquivalent, Pn = 1000(1.10n)
Aus diesem können wir schnell die Anzahl der Fische in 10, 20 oder 30 Jahren berechnen:
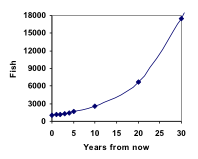
P10 = 1.1010(1000) = 2594
P20 = 1.1020(1000) = 6727
P30 = 1.1030(1000) = 17449
Wenn wir diese Werte in unser Diagramm eintragen, ergibt sich eine Form, die definitiv nicht linear ist. Wenn unsere Fischpopulation linear um 100 Fische pro Jahr gewachsen wäre, hätte die Population in 30 Jahren nur 4000 Fische erreicht, im Vergleich zu fast 18.000 bei diesem prozentualen Wachstum, das als exponentielles Wachstum bezeichnet wird.
Ein Video, das das explizite Modell dieser Fischgeschichte demonstriert, kann hier angesehen werden:
Bei exponentiellem Wachstum wächst die Population proportional zur Größe der Population, d.h. wenn die Population größer wird, führt das gleiche prozentuale Wachstum zu einem größeren zahlenmäßigen Wachstum.
Exponentielles Wachstum
Wenn eine Menge bei der Größe P0 beginnt und in jeder Zeitperiode um R% (geschrieben als Dezimalzahl, r) wächst, dann kann die Menge nach n Zeitperioden mit Hilfe einer dieser beiden Beziehungen bestimmt werden:
Rekursive Form
Pn = (1+r) Pn-1
Explizite Form
Pn = (1+r)n P0 oder äquivalent, Pn = P0 (1+r)n
Wir nennen r die Wachstumsrate.
Der Ausdruck (1+r) wird als Wachstumsmultiplikator oder allgemeiner Quotient bezeichnet.
Beispiel
Zwischen 2007 und 2008 wuchs Olympia, WA, um fast 3 % auf eine Bevölkerung von 245 Tausend Menschen. Wenn sich diese Wachstumsrate fortsetzt, wie hoch wäre die Einwohnerzahl von Olympia im Jahr 2014?
Das folgende Video erklärt dieses Beispiel im Detail.
Auswerten von Exponenten auf dem Taschenrechner
Um Ausdrücke wie (1,03)6 auszuwerten, wird es einfacher sein, einen Taschenrechner zu benutzen, als 1,03 sechsmal mit sich selbst zu multiplizieren. Die meisten wissenschaftlichen Taschenrechner haben eine Taste für Exponenten. Sie ist in der Regel folgendermaßen beschriftet:
^ , yx , oder xy .
Um 1,036 auszuwerten, tippen wir 1,03 ^ 6, oder 1,03 yx 6. Probieren Sie es aus – Sie sollten eine Antwort um 1,1940523 erhalten.
Versuchen Sie es
Indien ist das zweitbevölkerungsreichste Land der Welt, mit einer Bevölkerung im Jahr 2008 von etwa 1,14 Milliarden Menschen. Die Bevölkerung wächst jedes Jahr um etwa 1,34 %. Wenn sich dieser Trend fortsetzt, wie hoch wird die Bevölkerung Indiens im Jahr 2020 sein?
Beispiele
Eine Freundin verwendet die Gleichung Pn = 4600(1,072)n, um die jährlichen Studiengebühren an einer örtlichen Hochschule vorherzusagen. Sie sagt, die Formel basiere auf den Jahren nach 2010. Was sagt diese Gleichung aus?
Dieses Beispiel lässt sich anhand der folgenden Tabelle veranschaulichen.
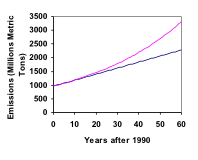
Im Jahr 1990 war der Energieverbrauch von Privathaushalten in den USA für 962 Millionen Tonnen Kohlendioxidemissionen verantwortlich. Bis zum Jahr 2000 ist diese Zahl auf 1182 Millionen Tonnen gestiegen. Wenn die Emissionen exponentiell ansteigen und mit der gleichen Rate fortgesetzt werden, wie hoch werden sie dann im Jahr 2050 sein?
Mehr über dieses Beispiel erfahren Sie hier.
Rundung
Ein Hinweis zur Rundung: Hätten wir die Wachstumsrate auf 2,1 % gerundet, wäre unsere Berechnung für die Emissionen im Jahr 2050 3347. Eine Rundung auf 2 % hätte unser Ergebnis auf 3156 geändert. Ein sehr kleiner Unterschied in den Wachstumsraten wird bei exponentiellem Wachstum stark vergrößert. Aus diesem Grund wird empfohlen, die Wachstumsrate so wenig wie möglich zu runden.
Wenn Sie runden müssen, behalten Sie mindestens drei signifikante Ziffern – Zahlen nach führenden Nullen. 0,4162 könnte also sinnvollerweise auf 0,416 gerundet werden. Eine Wachstumsrate von 0,001027 könnte sinnvollerweise auf 0,00103 gerundet werden.
Wurzeln mit dem Taschenrechner auswerten
Im vorherigen Beispiel mussten wir die 10. Wurzel einer Zahl berechnen. Das ist etwas anderes als die einfache Quadratwurzel, √. Viele wissenschaftliche Taschenrechner haben eine Taste für allgemeine Wurzeln. Sie ist in der Regel folgendermaßen beschriftet:
\sqrt{x}
Um zum Beispiel die 3. Wurzel aus 8 zu berechnen, geben wir entweder 3 \sqrt{{}} 8, oder 8 \sqrt{{}} 3, je nach Taschenrechner. Probieren Sie es auf Ihrem Rechner aus, um zu sehen, was zu verwenden ist – Sie sollten eine Antwort von 2 erhalten.
Wenn Ihr Rechner keine allgemeine Wurzeltaste hat, ist noch nicht alles verloren. Sie können stattdessen die Eigenschaft der Exponenten verwenden, die besagt, dass:
\sqrt{a}={a}^{\frac{1}{2}}.
Um die dritte Wurzel aus 8 zu berechnen, könnten Sie also die Exponententaste Ihres Rechners verwenden, um 81/3 auszuwerten. Geben Sie dazu ein:
8 yx ( 1 ÷ 3 )
Die Klammern sagen dem Rechner, dass er 1/3 dividieren soll, bevor er den Exponenten berechnet.
Versuchen Sie es
Die Zahl der Nutzer einer Social-Networking-Site betrug im Februar, als sie offiziell an die Börse ging, 45 Tausend und wuchs bis Oktober auf 60 Tausend. Wenn die Seite exponentiell wächst und das Wachstum mit der gleichen Rate anhält, wie viele Nutzer sind dann zwei Jahre nach dem Börsengang zu erwarten?
Beispiel
Wie hoch wären die Kohlenstoffemissionen im Jahr 2050, wenn die Emissionen linear mit der gleichen Rate wachsen würden, wie im letzten Beispiel?
Eine Demonstration dieses Beispiels ist im folgenden Video zu sehen.
Woher wissen wir also, welches Wachstumsmodell wir bei der Arbeit mit Daten verwenden sollen? Es gibt zwei Ansätze, die nach Möglichkeit zusammen verwendet werden sollten:
- Finden Sie mehr als zwei Daten. Zeichnen Sie die Werte auf und suchen Sie nach einem Trend. Scheinen sich die Daten wie eine Linie zu verändern, oder scheinen sich die Werte nach oben zu wölben?
- Betrachten Sie die Faktoren, die zu den Daten beitragen. Handelt es sich um Faktoren, von denen Sie erwarten würden, dass sie sich linear oder exponentiell verändern? Im Falle der Kohlenstoffemissionen könnte man zum Beispiel erwarten, dass sie in Ermangelung anderer Faktoren eng an die Bevölkerungswerte gebunden sind, die sich tendenziell exponentiell verändern.