Výstupy z učení

  • Určit, zda data nebo scénář popisují lineární nebo geometrický růst
  • Identifikovat tempo růstu, počáteční hodnoty nebo bodové hodnoty vyjádřené slovně, graficky, nebo číselně, a převést je do formátu použitelného pro výpočet
  • Vypočítat rekurentní a explicitní rovnice pro lineární a geometrický růst za předpokladu dostatečných informací a použít tyto rovnice k předpovědím

Konstantní rychlost změny je definičním znakem lineárního růstu. Při vykreslení dvojic souřadnic spojených s konstantní změnou získáme přímku, tedy tvar lineárního růstu. V této části budeme formalizovat způsob popisu lineárního růstu pomocí matematických termínů a pojmů. Na konci této části budete schopni napsat rekurentní i explicitní rovnice pro lineární růst zadaný výchozími podmínkami nebo konstantou změny. Budete také schopni rozpoznat rozdíl mezi lineárním a geometrickým růstem vzhledem ke grafu nebo rovnici.

Lineární (algebraický) růst

Předpovídání růstu

Marco je sběratel starožitných lahví od limonády. Jeho sbírka v současné době obsahuje 437 lahví. Každý rok si do rozpočtu vyčlení dostatek peněz na nákup 32 nových lahví. Můžeme určit, kolik lahví bude mít za 5 let a jak dlouho bude trvat, než jeho sbírka dosáhne 1000 lahví?“

Ačkoli byste pravděpodobně mohli obě tyto otázky vyřešit bez rovnice nebo formální matematiky, budeme náš přístup k tomuto problému formalizovat, abychom získali prostředky k zodpovězení složitějších otázek.

Předpokládejme, že Pn představuje počet nebo populaci lahví, které má Marco po n letech. P0 by tedy představovalo počet lahví nyní, P1 by představovalo počet lahví po 1 roce, P2 by představovalo počet lahví po 2 letech atd. Změnu Marcovy sbírky lahví bychom mohli popsat pomocí:

P0 = 437

Pn = Pn-1 + 32

Tomu se říká rekurentní vztah. Rekurzivní vztah je vzorec, který vztahuje další hodnotu v posloupnosti k předchozím hodnotám. Zde lze počet lahví v roce n zjistit přičtením 32 k počtu lahví v předchozím roce, Pn-1. Pomocí tohoto vztahu bychom mohli vypočítat:

P1 = P0 + 32 = 437 + 32 = 469

P2 = P1 + 32 = 469 + 32 = 501

P3 = P2 + 32 = 501 + 32 = 533

P4 = P3 + 32 = 533 + 32 = 565

P5 = P4 + 32 = 565 + 32 = 597

Zodpověděli jsme otázku, kolik lahví bude mít Marco za 5 let.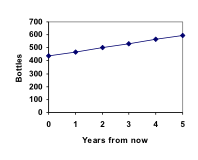

Řešení toho, za jak dlouho jeho sbírka dosáhne 1000 lahví, by však vyžadovalo mnohem více výpočtů.

Ačkoli jsou rekurentní vztahy vynikající pro jednoduchý a přehledný popis toho, jak se nějaká veličina mění, nejsou vhodné pro vytváření předpovědí nebo řešení problémů, které sahají daleko do budoucnosti. K tomu je vhodnější uzavřený nebo explicitní tvar vztahu. Explicitní rovnice nám umožňuje vypočítat Pn přímo, aniž bychom museli znát Pn-1. I když explicitní rovnici již možná dokážete odhadnout, odvodíme ji z rekurentního vzorce. Můžeme tak učinit selektivním nezjednodušováním za pochodu:

P1 = 437 + 32 = 437 + 1(32)

P2 = P1 + 32 = 437 + 32 + 32 = 437 + 2(32)

P3 = P2 + 32 = (437 + 2(32)). + 32 = 437 + 3(32)

P4 = P3 + 32 = (437 + 3(32)) + 32 = 437 + 4(32)

Snad už vidíte vzorec a zobecníte, že

Pn = 437 + n(32) = 437 + 32n

Pomocí této rovnice můžeme vypočítat, kolik lahví bude mít po pěti letech:

P5 = 437 + 32(5) = 437 + 160 = 597

Nyní můžeme také vyřešit, kdy sbírka dosáhne 1000 lahví, když za Pn dosadíme 1000 a vyřešíme n

1000 = 437 + 32n

563 = 32n

n = 563/32 = 17.59

Takže Marco dosáhne 1000 lahví za 18 let.

Kroky určení vzorce a řešení úlohy Marcovy sbírky lahví jsou podrobně vysvětleny v následujících videích.

V tomto příkladu rostla Marcova sbírka každý rok o stejný počet lahví. Tato neustálá změna je definičním znakem lineárního růstu. Vyneseme-li do grafu hodnoty, které jsme vypočítali pro Marcovu sbírku, vidíme, že hodnoty tvoří přímku, tedy tvar lineárního růstu.

Lineární růst

Pokud množství začíná na velikosti P0 a roste o d v každém časovém období, pak množství po n časových obdobích lze určit pomocí některého z těchto vztahů:

Rekurzivní tvar

Pn = Pn-1 + d

Explicitní tvar

Pn = P0 + d n

V této rovnici d představuje společný rozdíl – množství, které se změní při každém přírůstku n o 1.

Vazba na předchozí učivo: Sklon a průsečík

Společný rozdíl d v naší lineární rovnici možná poznáte jako sklon. Ve skutečnosti by vám celá explicitní rovnice měla být povědomá – jedná se o stejnou lineární rovnici, kterou jste se učili v algebře, pravděpodobně uvedenou jako y = mx + b.

Ve standardní algebraické rovnici y = mx + b bylo b průsečíkem y neboli hodnotou y, když x bylo nulové. Ve tvaru rovnice, který používáme, používáme k vyjádření této počáteční hodnoty P0.

V rovnici y = mx + b si připomeňme, že m byl sklon. Možná si to pamatujete jako „nárůst nad rozběhem“ nebo jako změnu y dělenou změnou x. Ať tak či onak, představuje to stejnou věc jako společný rozdíl d, který používáme – množství, o které se změní výstup Pn, když se vstup n zvětší o 1.

Rovnice y = mx + b a Pn = P0 + d n znamenají totéž a lze je použít stejnými způsoby. Jen je zapisujeme poněkud jinak.

Příklady

Populace losů v národním lese byla v roce 2003 změřena na 12 000 kusů a v roce 2007 byla opět změřena na 15 000 kusů. Pokud populace nadále poroste lineárně tímto tempem, jaká bude populace losů v roce 2014?

Zobrazit řešení

Na začátek musíme definovat, jak budeme měřit n. Nezapomeňte, že P0 je populace, když n = 0, takže pravděpodobně nebudeme chtít doslova použít rok 0. Jaký bude počet losů v roce 2014? Protože již známe počet obyvatel v roce 2003, definujme n = 0 jako rok 2003.

Tedy P0 = 12 000.

Dále musíme zjistit d. Pamatujte, že d je růst za časové období, v tomto případě růst za rok. Mezi oběma měřeními vzrostl počet obyvatel o 15 000-12 000 = 3 000, ale k takovému růstu bylo zapotřebí let 2007-2003 = 4 roky. Chceme-li zjistit přírůstek za rok, můžeme jej vydělit: 3 000 losů / 4 roky = 750 losů za 1 rok.

Alternativně můžete k určení společného rozdílu použít vzorec pro sklon z algebry, přičemž si všimněte, že populace je výstupem vzorce a čas je vstupem.

d=slope=\frac{\text{změnavýstupu}}{\text{změnavstupu}}=\frac{15 000-12 000}{2007-2003}=\frac{3000}{4}=750

Naši rovnici nyní můžeme zapsat v libovolném tvaru.

Rekurzivní tvar

P0 = 12 000

Pn = Pn-1 + 750

Explicitní tvar

Pn = 12 000 + 750(n)

Pro zodpovězení otázky si musíme nejprve uvědomit, že rok 2014 bude n = 11, protože rok 2014 je 11 let po roce 2003. Pro tento výpočet bude jednodušší použít explicitní tvar:

P11 = 12 000 + 750(11) = 20 250 losů

Více o tomto příkladu se dozvíte zde.

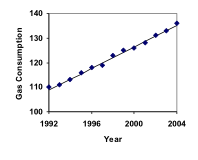
Spotřeba benzinu v USA neustále roste. Údaje o spotřebě v letech 1992 až 2004 jsou uvedeny níže. Najděte model pro tato data a použijte jej k předpovědi spotřeby v roce 2016. Pokud bude tento trend pokračovat, kdy spotřeba dosáhne 200 miliard galonů?

.

Rok ’92 ’93 ’94 ’95 ’96 ’97 ’98 ’99 ’00 ’01 ’02 ’03 ’04
Spotřeba (mld. galonů) 110 111 113 116 118 119 123 125 126 128 131 133 136
Zobrazit řešení

Kreslení těchto dat, se zdá, že je mezi nimi přibližně lineární vztah:

Ačkoli existují pokročilejší statistické techniky, které lze použít k nalezení rovnice pro modelování těchto dat, abychom získali představu o tom, co se děje, můžeme najít rovnici pomocí dvou částí dat – třeba dat z let 1993 a 2003.

Pokud by n = 0 odpovídalo roku 1993, dostali bychom P0 = 111 miliard galonů.

Pro zjištění d potřebujeme vědět, o kolik se spotřeba plynu v průměru každý rok zvýšila. Od roku 1993 do roku 2003 se spotřeba plynu zvýšila ze 111 miliard galonů na 133 miliard galonů, což představuje celkovou změnu 133 – 111 = 22 miliard galonů za 10 let. To nám dává průměrnou změnu 22 miliard galonů / 10 let = 2,2 miliardy galonů ročně.

Ekvivalentně,

d=slope=\frac{\text{změnavýstupu}}{\text{změnavstupu}}=\frac{133-111}{10-0}=\frac{22}{10}=2.2miliardy galonů za rok

Naši rovnici nyní můžeme zapsat v libovolném tvaru, který preferujeme.

Rekurzivní tvar

P0 = 111

Pn = Pn-1 + 2.2

Explicitní tvar

Pn = 111 + 2,2n

Vypočítání hodnot pomocí explicitního tvaru a jejich vynesení do grafu s původními daty ukazuje, jak dobře náš model odpovídá datům.

Našeho modelu nyní můžeme využít k předpovědím do budoucna za předpokladu, že se předchozí trend nezmění. Pro předpověď spotřeby benzinu v roce 2016:

n = 23 (2016 – 1993 = o 23 let později)

P23 = 111 + 2,2(23) = 161,6

Náš model předpovídá, že USA budou spotřebovávat 161,6

.6 miliard galonů benzinu v roce 2016, pokud bude současný trend pokračovat.

Chceme-li zjistit, kdy spotřeba dosáhne 200 miliard galonů, nastavíme Pn = 200 a vyřešíme n:

Pn = 200 Nahraďte Pn naším modelem

111 + 2.2n = 200 Od obou stran odečteme 111

2,2n = 89 Obě strany vydělíme 2,2

n = 40,4545

To nám říká, že spotřeba dosáhne 200 miliard přibližně 40 let po roce 1993, což by bylo v roce 2033.

Postupy, jak k této odpovědi dojít, jsou podrobně popsány v následujícím videu.

Náklad v dolarech na členství v posilovně na n měsíců lze popsat jednoznačnou rovnicí Pn = 70 + 30n. Co nám tato rovnice říká?

Zobrazit řešení

Hodnota P0 v této rovnici je 70, takže počáteční počáteční náklady jsou 70 dolarů. To nám říká, že za vstup do posilovny musí být iniciační nebo počáteční poplatek 70 $.

Hodnota pro d v této rovnici je 30, takže náklady se každý měsíc zvyšují o 30 $. To nám říká, že měsíční poplatek za členství v posilovně je 30 dolarů měsíčně.

Vysvětlení tohoto příkladu je podrobně popsáno níže.

Zkuste to

Počet otců v domácnosti v Kanadě neustále roste. I když tento trend není dokonale lineární, je poměrně lineární. Použijte údaje z let 1976 a 2010 k nalezení jednoznačného vzorce pro počet otců v domácnosti a poté jej použijte k předpovědi počtu v roce 2020.

Rok 1976 1984 1991 2000 2010
# of Stay -at-otců doma 20610 28725 43530 47665 53555
Zobrazit řešení

Nechť n= 0 odpovídá roku 1976, pak P_0= 20 610.
Od roku 1976 do roku 2010 se počet otců v domácnosti zvýšil o 53 555 – 20 610 = 32 945
To se stalo v průběhu 34 let, což dává společný rozdíl d 32 945 / 34 = 969.
P_n= 20,610 + 969n
Předpokládáme-li pro rok 2020, použijeme n = 44, P(44) = 20,610 + 969(44) = 63 246 otců v domácnosti v roce 2020.

Když se dobré modely pokazí

Při používání matematických modelů k předpovídání budoucího chování je důležité mít na paměti, že jen velmi málo trendů bude pokračovat donekonečna.

Příklad

Předpokládejme, že čtyřletý chlapec měří v současné době 39 palců a je vám řečeno, že má růst 2,5 palce ročně.

Můžeme sestavit model růstu, přičemž n = 0 odpovídá věku 4 let.

Rekurzivní tvar

P0 = 39

Pn = Pn-1 + 2,5

Explicitní tvar

Pn = 39 + 2. To znamená, že n = 0 odpovídá věku 4 let.5(n)

V šesti letech bychom tedy očekávali, že bude vysoký

P2 = 39 + 2,5(2) = 44 palců

Každý matematický model se nakonec zhroutí. Rozhodně bychom neměli očekávat, že tento chlapec bude růst stejným tempem po celý život. Kdyby tomu tak bylo, v padesáti letech by byl

P46 = 39 + 2,5(46) = 154 palců vysoký = 12,8 stop vysoký!“

Při použití jakéhokoli matematického modelu musíme zvážit, které vstupy je rozumné použít. Kdykoli extrapolujeme nebo děláme předpovědi do budoucna, předpokládáme, že model bude platit i nadále.

Vysvětlení tohoto rozdělení lineárního růstového modelu na videu si můžete prohlédnout zde.

Exponenciální (geometrický ) růst

Růst populace

Předpokládejme, že každý rok má pouze 10 % ryb v jezeře přeživší potomstvo. Jestliže v loňském roce bylo v jezeře 100 ryb, nyní by jich bylo 110. Pokud bylo loni v jezeře 1000 ryb, bylo by jich nyní 1100. Pokud neexistují žádné brzdící faktory, populace lidí a zvířat mají tendenci každoročně růst o procento stávající populace.


Předpokládejme, že naše jezero začínalo s 1000 rybami a 10 % ryb má každý rok přeživší potomstvo. Protože začínáme s 1000 rybami, P0 = 1000. Jak vypočítáme P1? Novou populací bude stará populace plus dalších 10 %. Symbolicky:

P1 = P0 + 0,10P0

Poznamenejme, že toto lze zkrátit na kratší formu pomocí faktoru:

P1 = P0 + 0,10P0 = 1P0 + 0,10P0 = (1+ 0,10)P0 = 1,10P0

Když 10 % je míra růstu, 1,10 je násobek růstu. Všimněte si, že 1,10 si můžeme představit jako „původních 100 % plus dalších 10 %“.

Pro naši populaci ryb,

P1 = 1,10(1000) = 1100

Můžeme tedy vypočítat populaci v pozdějších letech:

P2 = 1,10P1 = 1,10(1100) = 1210

P3 = 1,10P2 = 1,10(1210) = 1331

Všimněte si, že v prvním roce vzrostla populace o 100 ryb, ve druhém roce o 110 ryb a ve třetím roce o 121 ryb.

Přestože dochází ke konstantnímu procentuálnímu růstu, skutečný přírůstek počtu ryb se každým rokem zvyšuje.

Při grafickém znázornění těchto hodnot vidíme, že tento růst nevypadá zcela lineárně.

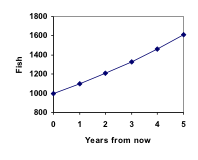
Procházku tímto rybím scénářem si můžete prohlédnout zde:

Abychom si udělali lepší představu o tom, jak tento procentuální růst ovlivňuje situaci, potřebujeme explicitní formu, abychom mohli rychle vypočítat hodnoty dále do budoucnosti.

Stejně jako u lineárního modelu začneme vycházet z rekurzivní rovnice:

P1 = 1,10(P0 )= 1,10(1000)

P2 = 1,10(P1 )= 1,10(1,10(1000)) = 1,102(1000)

P3 = 1.10(P2 )= 1.10(1.102(1000)) = 1.103(1000)

P4 = 1.10(P3 )= 1.10(1.103(1000)) = 1.104(1000)

Při pozorování vzoru můžeme zobecnit explicitní tvar na:

Pn = 1.10n(1000), nebo ekvivalentně Pn = 1000(1.10n)

Z toho můžeme rychle vypočítat počet ryb za 10, 20 nebo 30 let:

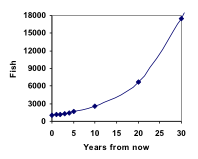
P10 = 1.1010(1000) = 2594

P20 = 1.1020(1000) = 6727

P30 = 1.1030(1000) = 17449

Přičtením těchto hodnot do našeho grafu zjistíme tvar, který rozhodně není lineární. Pokud by naše rybí populace rostla lineárně, tedy o 100 ryb ročně, dosáhla by za 30 let pouze 4000 kusů, zatímco při tomto růstu založeném na procentech, kterému se říká exponenciální růst, by dosáhla téměř 18 000 kusů.

Video demonstrující explicitní model tohoto rybího příběhu si můžete prohlédnout zde:

Při exponenciálním růstu roste populace úměrně velikosti populace, takže jak se populace zvětšuje, stejný procentuální růst přinese větší číselný růst.

Exponenciální růst

Pokud nějaká veličina začíná na velikosti P0 a každou časovou periodu roste o R % (zapsáno jako desetinné číslo, r), pak lze veličinu po n časových periodách určit pomocí některého z těchto vztahů:

Rekurzivní tvar

Pn = (1+r) Pn-1

Explicitní tvar

Pn = (1+r)n P0 nebo ekvivalentně Pn = P0 (1+r)n

R nazýváme mírou růstu.

Výraz (1+r) se nazývá růstový multiplikátor nebo běžný poměr.

Příklad

Město Olympia ve státě Washington vzrostlo mezi lety 2007 a 2008 o téměř 3 % na 245 tisíc obyvatel. Pokud by toto tempo růstu pokračovalo, kolik obyvatel by měla Olympia v roce 2014?

Ukázat řešení

Stejně jako dříve musíme nejprve určit, který rok bude odpovídat n = 0. Protože známe počet obyvatel v roce 2008, dávalo by smysl, aby rok 2008 odpovídal n = 0, tedy P0 = 245 tisíc. Rok 2014 by pak byl n = 6.

Víme, že míra růstu je 3 %, což dává r = 0,03.

Při použití explicitního tvaru:

P6 = (1+0,03)6 (245 000) = 1,19405(245 000) = 292 542,25

Model předpovídá, že v roce 2014 bude mít Olympia přibližně 293 tisíc obyvatel.

Následující video podrobně vysvětluje tento příklad.

Vyhodnocování exponentů na kalkulačce

Pro vyhodnocení výrazů jako (1,03)6 bude jednodušší použít kalkulačku než šestkrát vynásobit 1,03 sebou samým. Většina vědeckých kalkulaček má tlačítko pro exponenty. Obvykle je označeno buď takto:

^ , yx , nebo xy .

Chceme-li vyhodnotit 1,036, zadáme 1,03 ^ 6, nebo 1,03 yx 6 . Vyzkoušejte si to – měli byste dostat odpověď přibližně 1,1940523.

Vyzkoušejte si to

Indie je druhou nejlidnatější zemí světa, v roce 2008 měla přibližně 1,14 miliardy obyvatel. Počet obyvatel roste každoročně přibližně o 1,34 %. Bude-li tento trend pokračovat, na kolik vzroste počet obyvatel Indie v roce 2020?“

Ukázat řešení

Při použití n = 0 odpovídající roku 2008 je P_12= (1+0,0134)12(1,14) = přibližně 1. Jaký bude počet obyvatel Indie v roce 2020?337 miliard lidí v roce 2020

Příklady

Přítel používá rovnici Pn = 4600(1,072)n k předpovědi ročního školného na místní vysoké škole. Říká, že vzorec vychází z let po roce 2010. Co nám tato rovnice říká?

Ukázat řešení

V rovnici je P0 = 4600, což je počáteční hodnota školného, když n = 0. To nám říká, že školné v roce 2010 bylo 4600 dolarů.

Násobek růstu je 1,072, takže míra růstu je 0,072, neboli 7,2 %. To nám říká, že se očekává, že školné poroste každý rok o 7,2 %.

Složíme-li to dohromady, můžeme říci, že školné v roce 2010 činilo 4 600 USD a očekává se, že poroste každý rok o 7,2 %.

Podívejte se na následující příklad, který je zpracován.

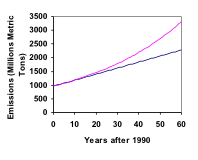
V roce 1990 byla spotřeba energie v domácnostech v USA zodpovědná za 962 milionů metrických tun emisí oxidu uhličitého. Do roku 2000 se toto číslo zvýšilo na 1182 milionů metrických tun. Pokud emise porostou exponenciálně a budou pokračovat stejným tempem, na jakou hodnotu vzrostou do roku 2050?

Ukázat řešení

Podobně jako dříve budeme n = 0 odpovídat roku 1990, protože to je rok prvního údaje, který máme k dispozici. To znamená, že P0 = 962 (milión metrických tun CO2). V této úloze nemáme uvedenu míru růstu, ale místo toho je dáno, že P10 = 1182.

Pokud je n = 10, vypadá explicitní rovnice takto:

P10 = (1+r)10 P0

Známe hodnotu pro P0, takže ji můžeme dosadit do rovnice:

P10 = (1+r)10 962

Víme také, že P10 = 1182, takže dosazením dostaneme

1182 = (1+r)10 962

Tuto rovnici nyní můžeme vyřešit pro rychlost růstu r. Začněte dělením 962.

\frac{1182}{962}={{(1+r)}^{10}}. Vezměte desátou odmocninu z obou stran

\sqrt{\frac{1182}{962}}=1+r Odečtěte 1 z obou stran

r=\sqrt{\frac{1182}{962}}-1=0,0208 = 2,08 %

Rostou-li tedy emise exponenciálně, rostou přibližně o 2,08 % ročně. Nyní můžeme předpovědět emise v roce 2050 tak, že zjistíme P60

P60 = (1+0,0208)60 962 = 3308,4 milionu tun CO2 v roce 2050

Další informace o tomto příkladu najdete zde.

Zaokrouhlování

Poznámka k zaokrouhlování: všimněte si, že pokud bychom míru růstu zaokrouhlili na 2,1 %, náš výpočet emisí v roce 2050 by byl 3347. Zaokrouhlením na 2 % by se náš výsledek změnil na 3156. Velmi malý rozdíl v míře růstu se při exponenciálním růstu značně zvětší. Z tohoto důvodu se doporučuje zaokrouhlovat míru růstu co nejméně.

Pokud potřebujete zaokrouhlovat, ponechte alespoň tři významné číslice – čísla za případnými počátečními nulami. Takže 0,4162 lze rozumně zaokrouhlit na 0,416. Míru růstu 0,001027 lze rozumně zaokrouhlit na 0,00103.

Vyhodnocení kořenů na kalkulačce

V předchozím příkladu jsme měli vypočítat desátou odmocninu čísla. To je něco jiného, než když vezmeme základní odmocninu √. Mnoho vědeckých kalkulaček má tlačítko pro obecné kořeny. Obvykle je označeno takto:

\sqrt{x}

Chceme-li například vyhodnotit 3. odmocninu z čísla 8, zadáme buď 3 \sqrt{{}} 8, nebo 8 \sqrt{{}}. 3, v závislosti na kalkulačce. Vyzkoušejte to na té své, abyste zjistili, co použít – měli byste dostat odpověď 2.

Pokud vaše kalkulačka nemá tlačítko pro obecnou odmocninu, není vše ztraceno. Místo toho můžete použít vlastnost exponentů, která říká, že:

\sqrt{a}={a}^{\frac{1}{2}}.

Pro výpočet 3. odmocniny z 8 tedy můžete použít tlačítko exponentu na kalkulačce a vyhodnotit 81/3.

. To provedete tak, že zadáte:

8 yx ( 1 ÷ 3 )

Závorky říkají kalkulačce, aby před provedením exponentu vydělila 1/3.

Zkuste to

Počet uživatelů jedné sociální sítě byl v únoru, kdy byla oficiálně zveřejněna, 45 tisíc a do října vzrostl na 60 tisíc. Pokud stránka roste exponenciálně a růst bude pokračovat stejným tempem, kolik uživatelů by měli očekávat dva roky poté, co vstoupili na veřejnost?“

Zobrazit řešení

Tady budeme měřit n v měsících, nikoli v letech, přičemž n = 0 odpovídá únoru, kdy vstoupili na veřejnost. To dává P_0= 45 tisíc. Říjen je o 8 měsíců později, takže P_8= 60.
P_8=(1+r)^{8}P_0
60=(1+r)^{8}45
\frac{60}{45}=(1+r)^8
\sqrt{\frac{60}{45}}=1+r
r=\sqrt{\frac{60}{45}}-1=0.0366\text{ nebo }3,66%
Obecná explicitní rovnice je P_n =(1,0366)^{n}45. Předpověď 24 měsíců po jejich zveřejnění dává P_{24}=(1,0366)^{24}45=106,63 tisíc uživatelů.

Příklad

Podíváme-li se zpět na poslední příklad, jaká by byla hodnota emisí uhlíku v roce 2050, kdyby emise rostly lineárně stejným tempem?

Zobrazit řešení

Znovu dostaneme n = 0 odpovídající roku 1990, čímž dostaneme P0 = 962. Proč? Abychom zjistili d, mohli bychom použít stejný přístup jako dříve a poznamenat, že emise vzrostly za 10 let o 220 milionů tun, což dává společný rozdíl 22 milionů tun každý rok.

Alternativně bychom mohli použít podobný přístup, který jsme použili k nalezení exponenciální rovnice. Při n = 10 vypadá explicitní lineární rovnice takto:

P10 = P0 + 10d

Známe hodnotu pro P0, takže ji můžeme dosadit do rovnice:

P10 = 962 + 10d

Jelikož víme, že P10 = 1182, dosazením dostaneme

1182 = 962 + 10d

Tuto rovnici nyní můžeme vyřešit pro společný rozdíl d.

1182 – 962 = 10d

220 = 10d

d = 22

To nám říká, že pokud se emise mění lineárně, rostou každý rok o 22 milionů tun. Předpovídáme-li emise v roce 2050,

P60 = 962 + 22(60) = 2282 milionů metrických tun.

Všimněte si, že toto číslo je podstatně menší než předpověď z modelu exponenciálního růstu. Výpočet a vykreslení dalších hodnot pomůže ilustrovat rozdíly.

Demonstraci tohoto příkladu můžete vidět na následujícím videu.

Jak tedy poznáme, který model růstu použít při práci s daty? Existují dva přístupy, které by se měly používat společně, kdykoli je to možné:

  1. Najděte více než dva údaje. Vykreslete hodnoty a hledejte trend. Zdá se, že se data mění jako přímka, nebo se zdá, že se hodnoty zakřivují směrem nahoru?“
  2. Zvažte faktory, které se na datech podílejí. Jsou to věci, u kterých byste očekávali, že se budou měnit lineárně nebo exponenciálně? Například v případě emisí uhlíku bychom mohli očekávat, že při absenci jiných faktorů budou úzce svázány s hodnotami populace, které mají tendenci měnit se exponenciálně.

.

By: adminPosted on

Napsat komentář

Vaše e-mailová adresa nebude zveřejněna.