Röntgendiffraktion är en vanlig teknik för materialkarakterisering som gör det möjligt att identifiera kristallinriktningar och interatomära avstånd. Röntgenstrålar används för detta eftersom våglängden ligger på samma längdskala som interatomära avstånd och värden för gitterparametrar.
Vad händer?
En röntgenstråle genereras i ett vakuumrör genom att en volframfilament värms upp förbi sin arbetsfunktion för att kasta ut elektroner. Vakuumförhållanden är nödvändiga för att öka elektronernas genomsnittliga fria väg. Elektronerna accelereras in i en kopparkatod med en energi i storleksordningen 25 keV. Elektronernas kollisioner med kopparkatoden resulterar i jonisering av det inre skalet, vilket ger upphov till röntgenstrålning när elektroner med högre energi sjunker ner för att fylla den lägre energiska vakansen. Elektroner från olika högre energinivåer faller ner och producerar elektromagnetiska vågor med varierande energi. På så sätt genereras röntgenstrålar med flera olika våglängder (av typen K-beta och K-alfa). För röntgendiffraktion är det idealiskt att ha monokromatiskt ljus som interagerar med provet, så K-beta-röntgenstrålarna filtreras bort med en nickelplatta. Även om det faktiskt finns två associerade K-alpha-energier är energierna så likartade att de inte påverkar den totala toppprofilen nämnvärt. Röntgenstrålarna passerar genom en kollimator för att justera strålbredden.
En liten bakgrund med Braggs lag
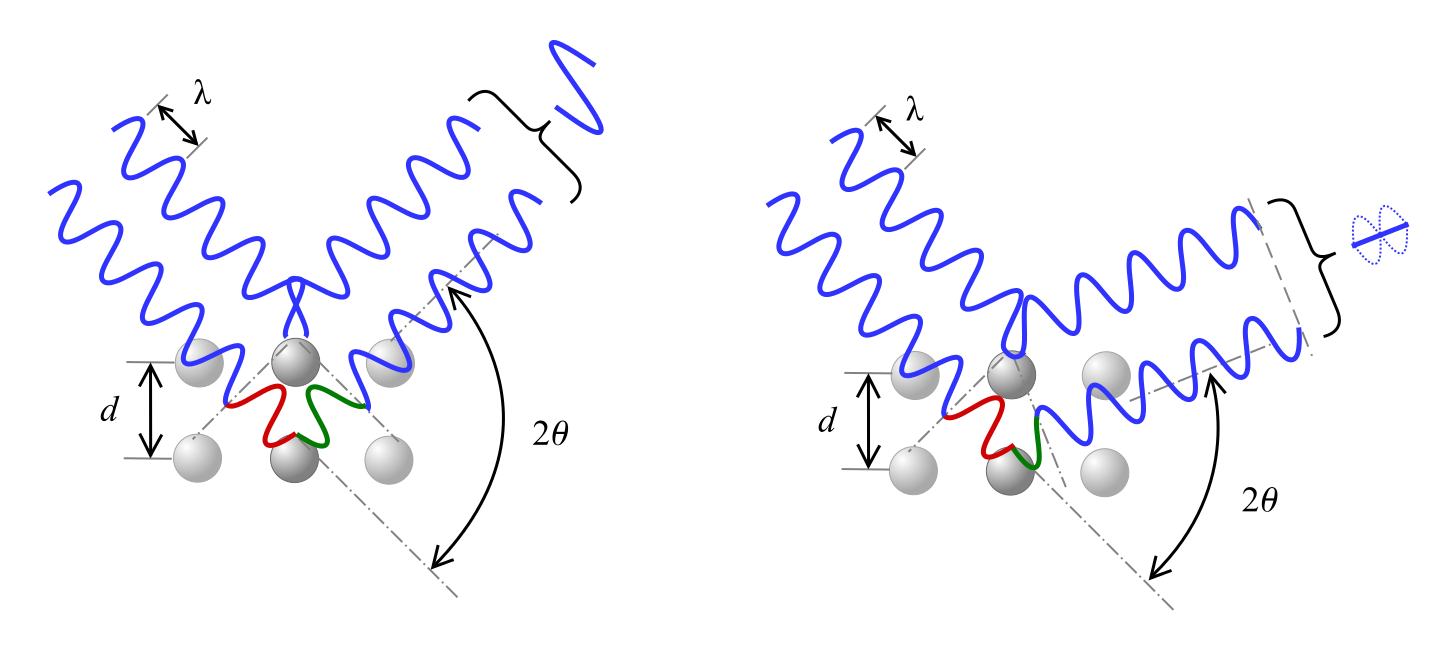
Braggs lag beskriver förhållandet för konstruktiv interferens, där röntgenstrålar med våglängden λ som faller in på materialet i vinkeln θ diffrakteras av kristallplan som är separerade med avståndet d och n representerar ett heltal.
Som visas se nedan orsakar en fasförskjutning i vågen antingen konstruktiv interferens, som visas till vänster, eller destruktiv interferens, som visas till höger, beroende på vinkeln 2θ.
Bekräftelser för tolkning av XRD-resultat
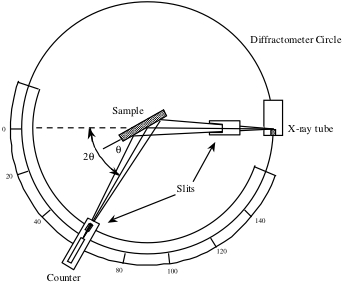
Torsken, som ses nedan i en schematisk bild av en röntgendiffraktometer, roteras över ett intervall av 2θ-värden och registrerar den röntgensignalintensitet som reflekteras från kristallen vid varje position. Denna intensitet som mäts som en funktion av 2θ används för att generera en toppprofil.
För vinklar som uppfyller Braggvillkoret kommer en topp i röntgensignalen att observeras på grund av den konstruktiva interferensen. Dessa toppar används sedan för att identifiera kristallriktningar och beräkna gitterparametrar. För kubiska system kan det interplanära avståndet, d, beräknas med hjälp av följande ekvation som härleds från kristallgeometrin, där a är gitterparametern och h, k och l är Miller-indexen.
Kombination av Braggs lag och det interplanära avståndet ger följande ekvation.
Här har vi flyttat alla konstanter till den vänstra sidan av ekvationen, vilket gör att vi kan jämföra förhållandet mellan sin2(θ)-värden och Miller-index mellan olika toppar.
När den infallande elektromagnetiska vågen träffar provmaterialet störs de elektroner som befinner sig i materialet i ett svängningsmönster, vilket genererar ny röntgenstrålning och effektivt sprider de infallande ljusvågorna. Två typer av spridning förekommer: koherent eller elastisk spridning innebär tätt bundna oscillerande elektroner som sprider röntgenstrålar med samma våglängd, och inkoherent spridning som sker när löst bundna elektroner sätts i oscillerande rörelse och genererar röntgenstrålar med olika energi. Röntgendiffraktion mäter intensiteten av koherent spridd röntgenstrålning, som når sin topp där vågorna interfererar på ett konstruktivt sätt. Den atomära spridningsfaktorn kan definieras som förhållandet mellan amplituden av den våg som sprids av en atom dividerad med amplituden av den våg som sprids av en enskild elektron. Detta förhållande beskriver i huvudsak en atoms spridningseffektivitet för en viss riktning.
Exempel på XRD-data
Här är data som samlats in från ett experiment som jag gjorde under min laborationskurs för grundutbildade studenter och som försökte identifiera en okänd metall baserat på dess kristallstruktur.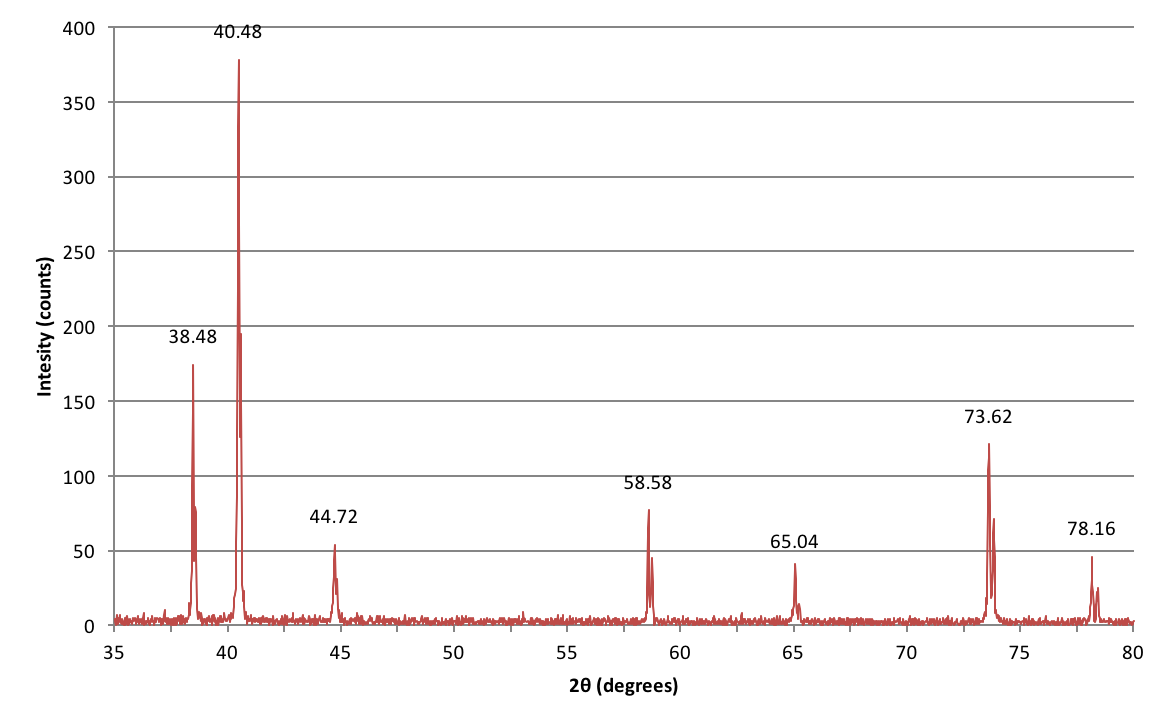
Hur ska jag tolka dessa toppar?
| Kristallstruktur | Villkor |
|---|---|
| Simple Cubic | alla h, k, l värden |
| Body Centered Cubic | h+k+l måste vara jämnt |
| Face Centered Cubic | h, k och l måste vara udda eller jämna |
Strukturfaktorer tar hänsyn till fall där ett plan kan finnas halvvägs mellan två angränsande plan och orsakar destruktiv interferens. Dessa faktorer resulterar i en uppsättning regler för olika kristallstrukturgeometrier som bestämmer när konstruktiv interferens kan uppstå. I tabellen ovan listas Miller-indexparametrarna där konstruktiv interferens kommer att uppstå. En mer omfattande tabell visas nedan. Genom att jämföra förhållandet mellan sin2θ (betecknat som $Q^2$ i den andra tabellen) för olika diffraktionstoppar kan kristallstrukturen och Miller-indexen bestämmas.
| Kristallplan (hkl) | $Q^2$ | Rymdgitter från vilka reflektioner är möjliga | |||||
|---|---|---|---|---|---|---|---|
| 100 | 1 | SC | |||||
| 110 | 2 | SC | BCC | ||||
| 111 | 3 | SC | FCC | DC | |||
| 200 | 4 | SC | BCC | FCC | |||
| 210 | 5 | SC | SC | ||||
| 211 | 6 | SC | BCC | ||||
| – | 7 | ||||||
| 220 | 8 | SC | BCC | FCC | DC | ||
| 300, 221 | 9 | SC | |||||
| 310 | 10 | SC | BCC | ||||
| 311 | 11 | SC | FCC | DC | |||
| 222 | 12 | SC | BCC | FCC | |||
| 320 | 13 | SC | |||||
| 321 | 14 | SC | BCC | ||||
| – | 15 | ||||||
| 400 | 16 | SC | BCC | FCC | DC | ||
X-Stråldiffraktion har ett brett spektrum av tillämpningar för materialkarakterisering. Den kan användas som en experimentell metod för att experimentellt bestämma volymen av en enhetscell för teoretiska densitetsberäkningar. Om materialet dessutom är utsatt för restspänning kommer det förvridna gittret att uppvisa en rad d-avstånd som uppfyller Braggs lag, vilket resulterar i mycket bredare diffraktionstoppar. Bredden på diffraktionstoppen kan också användas för att bestämma partikelstorleken.