Quadratsignaler, även kallade IQ-signaler, IQ-data eller IQ-prov, används ofta i RF-tillämpningar. De utgör grunden för komplex modulation och demodulering av komplexa RF-signaler, både i hårdvara och mjukvara, samt för komplexa signalanalyser. Det här inlägget tar upp begreppet IQ-signaler och hur de används.
Ett par periodiska signaler sägs vara i ”kvadratur” när de skiljer sig i fas med 90 grader. Den ”i fas” eller referenssignalen kallas ”I”, och signalen som är förskjuten med 90 grader (signalen i kvadratur) kallas ”Q”. Vad betyder detta och varför bryr vi oss? Låt oss bryta ner det genom att börja med några grunder.
Grunderna för RF-modulation
Jag börjar med en genomgång enkel RF-modulation. En omodulerad RF-bärare är helt enkelt en sinusvåg som visas nedan.
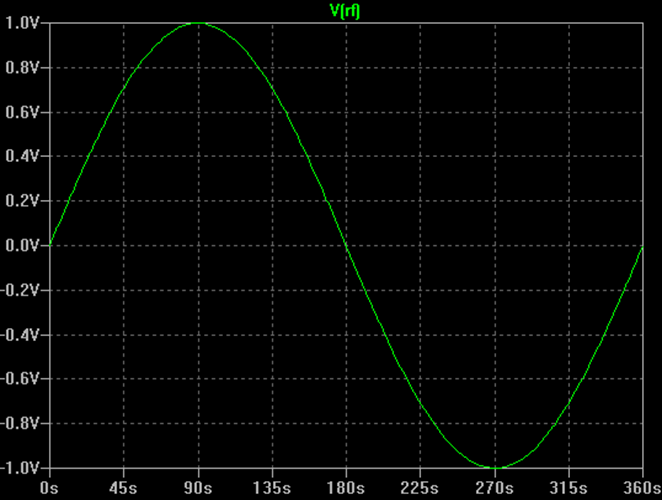
Signalen kan beskrivas som en funktion av tiden genom följande ekvation:
V(t) = A * sin (2 * π * f * t + Ф)
där:
A: är toppamplituden
f: är frekvensen
t: är tiden
Ф: är fasförskjutningen
Information ”transporteras” av en RF-bärare genom modulationsprocessen. Informationssignalen (röst, data osv.) används för att ändra egenskaperna hos RF-signalen. Ett enkelt exempel är amplitudmodulering eller AM.
För AM används informationssignalen för att ändra eller modulera bärarens amplitud. Matematiskt kan det representeras genom att ändra konstanten ”A” i föregående ekvation till någon tidsvarierande signal (informationssignalen):
V(t) = A(t) * sin (2 * π * f * t + Ф)
Informationssignalen, även känd som basbandssignalen, varierar mycket långsammare med tiden än vad RF-signalen gör. För att se effekten av modulationen måste man därför observera RF-signalens kuvert över en längre tidsskala som visas nedan.
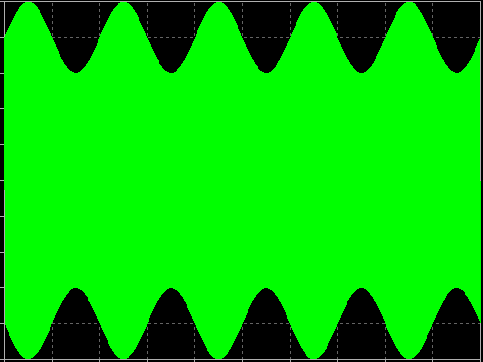
I det här fallet är A(t)-signalen en sinusoid. Figuren visar hur amplituden av RF-signalen följer den sinusformade A(t)-basbandssignalen.
Du kan utöka detta genom att inse att andra egenskaper hos RF-bäraren kan ändras, eller moduleras, av en basbandssignal över tiden. Om frekvensen moduleras av en basbandssignal har man frekvensmodulering (FM). Om fasen moduleras har man på samma sätt fasmodulering (PM). Således:
- A(t) är när amplituden varieras mot tiden
- f(t) är när frekvensen varieras mot tiden
- Ф(t) är när fasen varieras mot tiden.
Håll dig det grundläggande begreppet modulering i minnet när vi knyter in begreppet kvadratsignaler…
Koncept för kvadratsignaler
Om fasskillnaden Ф mellan två sinusoider är 90 grader (eller π /2 radianer), sägs dessa två signaler vara i kvadratur. Ett exempel på detta är sinusvågen och cosinusvågen.
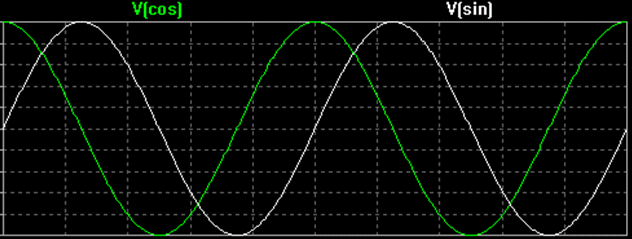
Enligt konvention är cosinusvågen faskomponent och sinusvågen kvadraturkomponent. Den stora bokstaven I representerar amplituden för infas-signalen och den stora bokstaven Q representerar amplituden för kvadratsignalen.
Användning av kvadratsignaler för att modulera
Interessanta saker händer när man tittar på hur man adderar kvadratsignaler tillsammans.
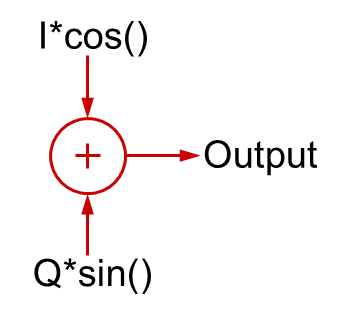
Om I = 1 och Q = 0 skulle man helt enkelt ha cosinusvågen (fas lika med 0). På samma sätt, om I=0 och Q=1, skulle du ha sinusvågen, vilket är den 90 grader förskjutna signalen.
Om både I och Q var lika med 1 blir summan en ny signal som visas grafiskt nedan.
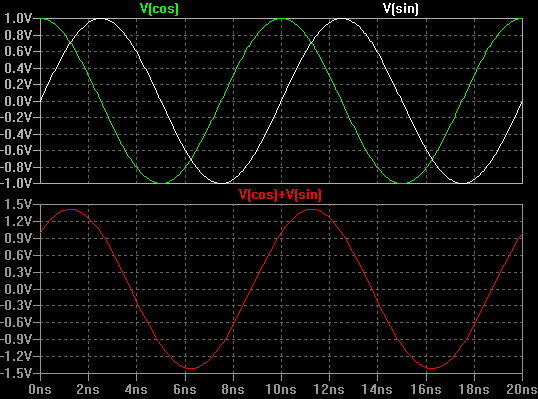
Bemärk att om man adderar dessa två kvadratsignaler med lika amplitud tillsammans, så resulterar det i en ny sinusoid som är fasförskjuten med 45 grader.
Nu kan du se att amplituden och fasen för summan av kvadratsignalerna är en funktion av värdet på I och Q. Därför kan du skapa modulerade RF-signaler genom att variera I- och Q-värdena i förhållande till tiden. Låt oss titta på några exempel.
Digitala RF-modulationsexempel
Om Q=0 och I ändras mellan +1 och -1 över tiden skapar du en binär fasförskjutningsnyckelad RF-signal (BPSK):
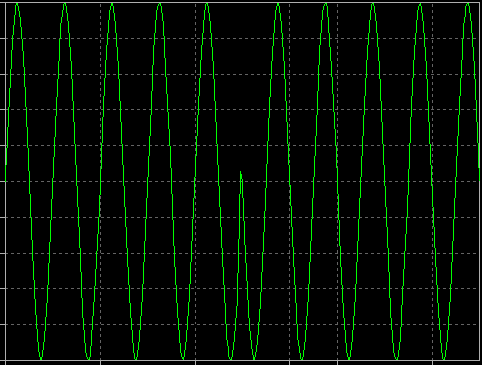
I(t)-signalen skulle kunna vara en enkel digital bitström. Om du låter den signalen styra förstärkningen av RF-sinusoiden mellan +1 och -1 har du skapat en BPSK-signal.
Om man tar detta ett steg längre… Om två digitala bitar används för att styra I- och Q-värdena mellan +1 och -1 över tiden, kan den resulterande summan av kvadratur-signalerna vara en av fyra olika faser:
- I=+1 & Q=+1 resulterar i 45 graders fas
- I=-1 & Q=+1 resulterar i 135 graders fas
- I=-1 & Q=-1 resulterar i 225 graders fas
- I=+1 & Q=-1 resulterar i 315 graders fas
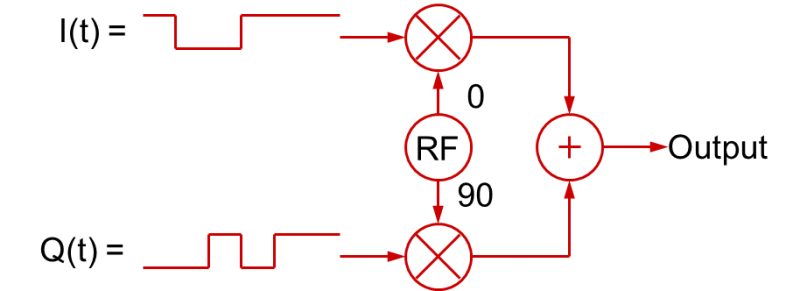
Detta kallas QPSK-modulering (Quadrature Phase Shift Keying). Detta är två exempel på kvadratisk amplitudmodulering (QAM). De olika modulationstillstånden för QAM visas ofta i ett konstellationsdiagram. Ett konstellationsdiagram är helt enkelt ett fasordiagram som visar amplituden och fasen hos en signal i form av ett polärt diagram.
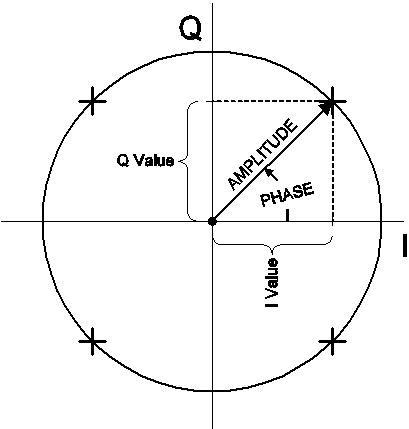
Vektorns längd från origo representerar signalens magnitud, och den vinkel som vektorn bildar med den horisontella axeln representerar fasen. De fyra ”tillstånden” för den QPSK-signal som beskrivs ovan visas som de fyra ”+”-symbolerna i diagrammet. Du noterar också att den horisontella axeln är märkt ”I” och att den vertikala axeln är märkt ”Q” – eftersom dessa representerar de I- och Q-komponentvärden som är förknippade med signalen.
Mer komplexa QAM-modulationer, såsom 16QAM, har helt enkelt fler tillstånd. För 16QAM kan I- och Q-värdena var och en ha ett av fyra diskreta värden, vilket ger 16 möjliga kombinationer. Detta resulterar i 16 kombinationer av amplitud och fas för RF-signalen.
Kvadratursignaler överallt
Användning av I- och Q-signaler som varierar över tiden för att skapa modulerade RF-signaler är inte begränsad till digitala basbandssignaler. I(t) och Q(t) basbandssignalerna kan också vara analoga basbandssignaler. i de flesta ”digitalt” modulerade RF-tillämpningar som QPSK eller nQAM filtreras basbandssignalerna för att sakta ner övergångarna. Detta görs för att begränsa den resulterande bandbredden för den modulerade RF-signalen (snabba digitala stignings- och falltider upptar mycket bandbredd!). Dessa filtrerade digitala signaler är i praktiken analoga signaler! Så i en mer allmän mening kan kvadraturmoduleringsprocessen illustreras enligt den här figuren:
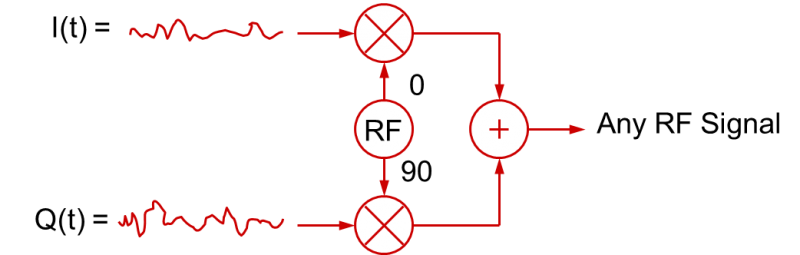
Den allmänna slutsatsen man kan dra av detta är att en RF-signal med vilken typ av modulering som helst kan skapas med lämpliga I(t)- och Q(t)-basbandssignaler (som i sin tur varierar amplituderna för cosinus- och sinusvågorna som summeras tillsammans).
Självfallet fungerar samma process i omvänd ordning för att demodulera en RF-signal. Genom att blanda en RF-signal med LO-signaler (lokal oscillator) i kvadratur kan I(t) och Q(t) basbandssignaler skapas.
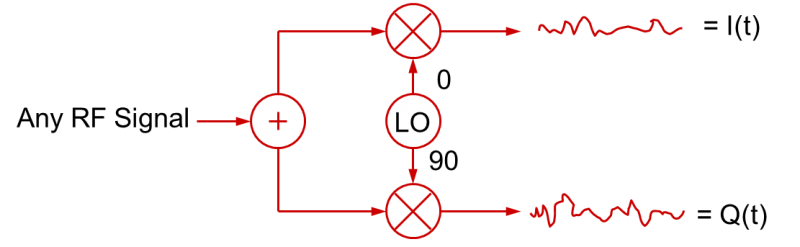
Detta är den grundläggande grunden för de flesta moderna RF-signaler för generering och modulering, liksom för demodulering och vektorsignalanalys.
Software Defined Radio (SDR) system använder dessa begrepp i stor utsträckning eftersom basband I & Q-signalerna ofta representeras som diskreta tidssamplade data. Därför kan digital signalbehandling (DSP) användas för att bokstavligen definiera sändar- och mottagaregenskaperna, inklusive filtrering, modulering och demodulering, AGC osv. SDR-mottagare har ofta en basbandsbandsbandbredd på några hundra kHz eller mer, vilket ger möjlighet att utföra en mängd olika funktioner, inklusive ”breda” bandskope- och spektrogramfunktioner, samt att samtidigt kunna övervaka och demodulera flera signaler av olika typer samtidigt.
Vektorsignalgeneratorer har en kvadraturmodulator som tar emot I(t)- och Q(t)-signaler, som den sedan använder för att amplitudmodulera ett par quadratur-sinusoider, som sedan summeras för att skapa den modulerade RF-utgången. Många vektorsignalgeneratorer har i allmänhet paneluttag där du kan ansluta dina egna IQ-signaler. Många har en intern basbands Arbitrary Waveform Generator (AWG) för att skapa basbands IQ-signaler.
Moderna Vector Signal Analyzers har vanligtvis bandbredder på 25, 40, 110 MHz eller mer. De omvandlar de inkommande RF-signalerna till deras I- och Q-komponenter. All analys (spektralanalys mot tiden, demodulering, pulsanalys etc.) är helt enkelt olika matematiska bearbetningar av samma IQ-data. Realtidssignalanalysatorer, t.ex. Tektronix RSA5000- och RSA6000-serier, har ytterligare möjlighet att ta emot ”levande” IQ-dataströmmar och utföra realtidsbehandling av data. Detta ger möjlighet att göra saker som att visualisera det levande spektrumet av en RF-signal, samt att kunna utlösa transienta händelser som kanske bara är synliga i frekvensdomänen.
Se Tektronix senaste utbud av spektrumanalysatorer.