Introduktion
Inom datavetenskap är en riktad acyklisk graf (DAG) en riktad graf utan cykler. I den här handledningen visar vi hur man gör en topologisk sortering på en DAG i linjär tid.
Topologisk sortering
I många tillämpningar använder vi riktade acykliska grafer för att ange prejudikat mellan händelser. I ett schemaläggningsproblem finns det till exempel en uppsättning uppgifter och en uppsättning begränsningar som anger ordningen för dessa uppgifter. Vi kan konstruera en DAG för att representera uppgifterna. De riktade kanterna i DAG:n representerar uppgifternas ordning.
Låt oss betrakta ett problem med hur en person kan klä sig för ett formellt tillfälle. Vi behöver ta på oss flera plagg, till exempel strumpor, byxor, skor osv. Vissa plagg måste tas på före de andra. Vi måste till exempel ta på oss strumporna före skorna. Vissa plagg kan tas på i vilken ordning som helst, t.ex. strumpor och byxor. Vi kan använda en DAG för att illustrera detta problem:
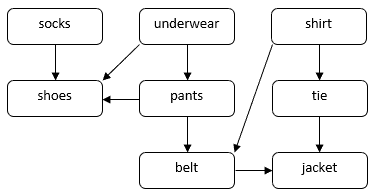
I denna DAG motsvarar vertikaler plagg. En direkt kant 
i DAG anger att vi måste ta på oss plagg 
före plagg 
. Vår uppgift är att hitta en ordning för att sätta på alla plagg samtidigt som vi respekterar beroendeställningarna. Vi kan till exempel ta på oss plaggen i följande ordning:
En topologisk sortering av en DAG 
är en linjär ordningsföljd för alla dess hörn så att om innehåller en kant , så visas före i ordningsföljden. För en DAG kan vi konstruera en topologisk sortering med en löptid som är linjär mot antalet hörn plus antalet kanter, vilket är 
.
Kahns algoritm
I en DAG har varje väg mellan två hörn en ändlig längd eftersom grafen inte innehåller någon cykel. Låt 
vara den längsta vägen från (källvertikal) till (målvertikal). Eftersom är den längsta vägen kan det inte finnas någon inkommande kant till . Därför innehåller en DAG minst en topp som inte har någon inkommande kant.
3.1. Kahns algoritm
I Kahns algoritm konstruerar vi en topologisk sortering av en DAG genom att hitta hörn som inte har några inkommande kanter:
I den här algoritmen beräknar vi först värdena för ingraden för alla hörn.
Därefter börjar vi med ett hörn vars ingrad är 0 och placerar det i slutet av utdatalistan. När vi väljer en hörnpunkt uppdaterar vi in-degree-värdena för dess angränsande hörnpunkter eftersom hörnpunkten och dess utkanter tas bort från grafen.
Vi kan upprepa ovanstående process tills vi väljer alla hörnpunkter. Utdragslistan är då en topologisk sortering av grafen.
3.2. Tidskomplexitet
För att beräkna in-degrees för alla hörn måste vi besöka alla hörn och kanter i . Därför är körtiden för beräkningar av ingrader. För att undvika att beräkna dessa värden på nytt kan vi använda en matris för att hålla reda på in-degree-värdena för dessa hörn. Inom while-slingan måste vi också besöka alla hörn och kanter. Därför är den totala körtiden .
Djup första sökning
Vi kan också använda en DFS-algoritm (Depth First Search) för att konstruera den topologiska sorteringen.
4.1. Graph DFS with Recursion
För att ta itu med den topologiska sorteringsaspekten med DFS börjar vi med att gå igenom en standardiserad, rekursiv DFS-traversal-algoritm för grafer:
I standard-DFS-algoritmen börjar vi med en slumpmässig vertex i och markerar denna vertex som besökt. Sedan anropar vi rekursivt funktionen dfsRecursive för att besöka alla dess obesökta angränsande hörn. På detta sätt kan vi besöka alla hörn i på tid.
Men eftersom vi lägger in varje hörn i listan omedelbart när vi besöker det, och eftersom vi kan börja vid vilket hörn som helst, kan den vanliga DFS-algoritmen inte garantera att den genererar en topologiskt sorterad lista.
Låt oss se vad vi måste göra för att komma till rätta med denna brist.
4.2. DFS-baserad topologisk sorteringsalgoritm
Vi kan modifiera DFS-algoritmen för att generera en topologisk sortering av en DAG. Under DFS-traverseringen, efter att alla grannar till en vertex har besökts, placerar vi den sedan längst fram i resultatlistan 
. På detta sätt kan vi se till att visas före alla sina grannar i den sorterade listan:
Denna algoritm liknar den vanliga DFS-algoritmen. Även om vi fortfarande börjar med en slumpmässig vertex, lägger vi inte in vertexen i listan omedelbart när vi besöker den. Istället besöker vi först alla dess grannar rekursivt och placerar sedan vertexen längst fram i listan. Om innehåller en kant visas därför före i listan.
Den totala körtiden är också , eftersom den har samma tidskomplexitet som DFS-algoritmen.
Slutsats
I den här artikeln visade vi ett exempel på topologisk sortering på en DAG. Dessutom diskuterade vi två algoritmer som kan göra en topologisk sortering på tid.
Javaimplementationen av den DFS-baserade topologiska sorteringsalgoritmen finns tillgänglig i vår artikel om Depth First Search in Java.