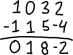Tillbaka till lektionsindexet | Gör lektionerna i ordning | Utskriftsvänlig sida
Matrisradoperationer (sida 1 av 2)
”Operationer” är ett matematiskt uttryck för ”procedurer”. De fyra ”grundläggande operationerna” på tal är addition, subtraktion, multiplikation och division. För matriser finns det tre grundläggande radoperationer, det vill säga det finns tre procedurer som man kan göra med raderna i en matris.
Den första operationen är radväxling. Till exempel, givet matrisen:

…kan du byta rader för att sätta matrisen i ett trevligare radarrangemang, så här:
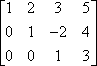
Radbyte indikeras ofta genom att rita pilar, så här:

När du byter rader ska du vara försiktig så att du kopierar posterna på rätt sätt.
Den andra operationen är radmultiplikation. Till exempel, med följande matris:

…kan du multiplicera den första raden med -1 för att få ett positivt ledande värde i den första raden:
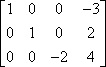
Denna radmultiplikation indikeras ofta med hjälp av en pil med multiplikationen listad ovanpå, så här:
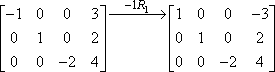
Den ”-1R1” indikerar den faktiska operationen. ”-1” säger att vi multiplicerade med minus ett; ”R1” säger att vi arbetade med den första raden. Observera att den andra och tredje raden kopierades ner, oförändrade, till den andra matrisen. Multiplikationen gällde bara den första raden, så posterna för de andra två raderna fördes bara med oförändrade.
Du kan multiplicera med vad du vill. För att till exempel få en ledande 1 i den tredje raden i den föregående matrisen kan du multiplicera den tredje raden med en negativ halva:

Då du inte gjorde något med den första och den andra raden, kopierades dessa poster bara över oförändrade till den nya matrisen.
Du kan göra mer än en radmultiplikation inom samma steg, så du kunde ha gjort de två ovanstående stegen i bara ett steg, så här:
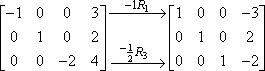
Det är en bra idé att använda någon form av notation (som pilarna och subscripts ovan) så att du kan hålla reda på ditt arbete. Matriser är väldigt röriga, särskilt om du gör dem för hand, och anteckningar kan göra det lättare att kontrollera ditt arbete senare. Det kommer också att imponera på din lärare.
Den sista radoperationen är radaddition. Radaddition liknar ”additionsmetoden” för att lösa system av linjära ekvationer. Anta att du har följande ekvationssystem:
x + 3y = 1
-x + y = 3 Copyright © Elizabeth Stapel 2003-2011 All Rights Reserved
Advertisement
Du skulle kunna börja lösa det här systemet genom att addera neråt i kolumnerna för att få 4y = 4:
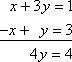
Du kan göra något liknande med matriser.Om du till exempel får följande matris:

…kan du ”minska” (få fler ledande nollor i) den andra raden genom att addera den första raden till den (det allmänna målet med matriser i det här skedet är att få en ”1” – eller ”nollor” och sedan en ”1” – i början av varje matrisrad). När du reducerade det linjära systemet med två ekvationer genom att addera, ritade du en ”likhetstecken” tvärs över botten och adderade neråt. När du använder addition på en matris behöver du ta fram lite klotterpapper, eftersom du inte vill försöka göra arbetet inuti matrisen. Så addera de två raderna på ditt klotterpapper:
|
Klipparbete – |
|
Det här är din nya andra rad; du kommer att skriva den i stället för den gamla andra raden. Resultatet kommer att se ut så här:
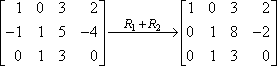
I det här fallet betyder ”R1 + R2” på pilen att ”jag lade till rad ett till rad två, och det här är resultatet jag fick”. Eftersom rad ett faktiskt inte ändrades, och eftersom vi inte gjorde något med rad tre, kopieras dessa rader oförändrade in i den nya matrisen.
Top | 1 | 2 | Tillbaka till index Nästa >>
|
Citera denna artikel som: |
Stapel, Elizabeth. ”Matrix Row Operations”. Purplemath. Tillgänglig från 2016
|