Klassificering med hjälp av diskriminantanalys
Låt oss se hur LDA kan användas som en övervakad klassificeringsmetod. Betrakta ett generiskt klassificeringsproblem: En slumpvariabel X kommer från en av K klasser, med vissa klasspecifika sannolikhetstätheter f(x). En diskriminantregel försöker dela upp datarummet i K disjunktionsområden som representerar alla klasser (tänk dig rutorna på ett schackbräde). Med dessa regioner innebär klassificering genom diskriminantanalys helt enkelt att vi tilldelar x till klass j om x befinner sig i region j. Frågan är då hur vi vet vilken region data x faller i? Naturligtvis kan Vi kan följa två tilldelningsregler:
- Maximal sannolikhetsregel: Om vi antar att varje klass kan förekomma med lika stor sannolikhet, så tilldela x till klass j om
- Bayesiansk regel: Om vi känner till klassens prioritets sannolikheter, π, så tilldela x till klass j om

Linjär och kvadratisk diskriminantanalys
Om vi antar att data kommer från en multivariat gaussisk fördelning, i.dvs. att fördelningen av X kan karakteriseras av dess medelvärde (μ) och kovarians (Σ), kan explicita former av ovanstående fördelningsregler erhållas. Enligt den Bayesianska regeln klassificerar vi data x till klass j om den har den högsta sannolikheten bland alla K klasser för i = 1,…,K:

Ovanstående funktion kallas diskriminantfunktion. Observera att log-likelihood används här. Med andra ord berättar diskriminantfunktionen hur sannolikt det är att data x tillhör varje klass. Beslutsgränsen som skiljer två klasser, k och l, är därför den mängd x där två diskriminantfunktioner har samma värde. Därför är alla data som faller på beslutsgränsen lika sannolika från de två klasserna (vi kunde inte bestämma oss).
LDA uppstår i det fall där vi antar lika stor kovarians mellan K klasser. Det vill säga, istället för en kovariansmatris per klass har alla klasser samma kovariansmatris. Då kan vi få följande diskriminantfunktion:

Bemärk att detta är en linjär funktion i x. Beslutsgränsen mellan ett par klasser är således också en linjär funktion i x, vilket är anledningen till dess namn: linjär diskriminantanalys. Utan antagandet om lika kovarians upphävs inte den kvadratiska termen i sannolikheten, varför den resulterande diskriminantfunktionen är en kvadratisk funktion i x:

I detta fall är beslutsgränsen kvadratisk i x. Detta kallas kvadratisk diskriminantanalys (QDA).
Vilket är bäst? LDA eller QDA?
I verkliga problem är populationsparametrarna vanligen okända och uppskattas från träningsdata som medelvärden och kovariansmatriser för urvalet. Medan QDA rymmer mer flexibla beslutsgränser jämfört med LDA, ökar också antalet parametrar som måste uppskattas snabbare än för LDA. För LDA behövs (p+1) parametrar för att konstruera diskriminantfunktionen i (2). För ett problem med K klasser skulle vi bara behöva (K-1) sådana diskriminantfunktioner genom att godtyckligt välja en klass som basklass (genom att subtrahera basklassens sannolikhet från alla andra klasser). Därför är det totala antalet uppskattade parametrar för LDA (K-1)(p+1).
För varje QDA-diskriminantfunktion i (3) måste däremot medelvärdesvektorn, kovariansmatrisen och klassprioriteten uppskattas:
– Medelvärde: p
– Kovarians: p(p+1)/2
– Klassprioritet: 1
För QDA måste vi på samma sätt skatta (K-1){p(p+3)/2+1} parametrar.
Följaktligen ökar antalet parametrar som uppskattas i LDA linjärt med p medan det för QDA ökar kvadratiskt med p. Vi skulle förvänta oss att QDA har sämre prestanda än LDA när problemdimensionen är stor.
Bäst av två världar? Kompromiss mellan LDA & QDA
Vi kan hitta en kompromiss mellan LDA och QDA genom att reglera de individuella klassernas kovariansmatriser. Regularisering innebär att vi lägger en viss begränsning på de uppskattade parametrarna. I det här fallet kräver vi att den individuella kovariansmatrisen krymper mot en gemensam poolad kovariansmatris genom en straffparameter, t.ex. α:

Den gemensamma kovariansmatrisen kan också regulariseras mot en identitetsmatris genom en straffparameter t.ex, β:

I situationer där antalet ingående variabler vida överstiger antalet stickprov kan kovariansmatrisen uppskattas dåligt. Krympning kan förhoppningsvis förbättra skattningen och klassificeringsnoggrannheten. Detta illustreras av figuren nedan.

Beräkning för LDA
Vi kan se från (2) och (3) att beräkningar av diskriminantfunktioner kan förenklas om vi först diagonaliserar kovariansmatriserna. Det vill säga, data transformeras så att de har en identisk kovariansmatris (ingen korrelation, varians 1). I fallet med LDA är det så här vi går tillväga med beräkningen:

Steg 2 sfäriserar data för att få fram en identitetskovariansmatris i det transformerade rummet. Steg 4 erhålls genom att följa (2).
Låt oss ta ett exempel med två klasser för att se vad LDA verkligen gör. Anta att det finns två klasser, k och l. Vi klassificerar x till klass k om

Ovanstående villkor innebär att det är mer troligt att klass k producerar data x än klass l. Genom att följa de fyra stegen ovan skriver vi
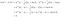
Det vill säga, Vi klassificerar data x i klass k om

Den härledda tilldelningsregeln avslöjar hur LDA fungerar. Den vänstra sidan (l.h.s.) av ekvationen är längden på den ortogonala projektionen av x* på det linjesegment som förenar de två klassmedelvärdena. Den högra sidan är placeringen av segmentets centrum korrigerad med hjälp av sannolikheterna för klassernas prioriteter. I huvudsak klassificerar LDA de sphered data till det närmaste klassmedelvärdet. Vi kan göra två observationer här:
- Beslutspunkten avviker från mittpunkten när klassprioritetssannolikheterna inte är desamma, dvs. gränsen förskjuts mot klassen med en mindre prioritetssannolikhet.
- Data projiceras på det utrymme som spänns upp av klassmedelvärdena (multiplikation av x* och medelvärdesubtraktion på regelns l.h.s.). Avståndsjämförelser görs sedan i detta utrymme.