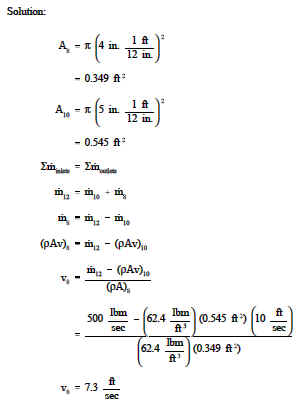Vätskeströmning Innehållsförteckning
Kunskap om hydraulik och pneumatik
Vätskekraftutrustning
Kontinuitetsekvation för vätskor
Kontinuitetsekvationen är helt enkelt ett matematiskt uttryck för principen om massans bevarande. För en kontrollvolym som har ett enda inlopp och ett enda utlopp säger principen om massans bevarande att massflödet in i volymen måste vara lika med massflödet ut ur volymen för ett stabilt flöde. Kontinuitetsekvationen för denna situation uttrycks genom ekvation 3-5.

För en kontrollvolym med flera in- och utlopp kräver principen om massans bevarande att summan av massflödet in i kontrollvolymen är lika med summan av massflödet ut ur kontrollvolymen. Kontinuitetsekvationen för denna mer allmänna situation uttrycks av ekvation 3-6.
![]()
En av de enklaste tillämpningarna av kontinuitetsekvationen är att bestämma förändringen i vätskehastighet på grund av en expansion eller kontraktion i ett rörs diameter.
Exempel: Exempel: Kontinuitetsekvation – Expansion av rör
Steady-state-flöde existerar i ett rör som genomgår en gradvis expansion från en diameter på 6 tum till en diameter på 8 tum. Vätskans densitet i röret är konstant på 60,8 lbm/ft3. Om flödeshastigheten är 22,4 ft/sek i sektionen 6 tum, vad är då flödeshastigheten i sektionen 8 tum?
Lösning:
Från kontinuitetsekvationen vet vi att massflödet i sektionen 6 tum måste vara lika med massflödet i sektionen 8 tum. Genom att låta subscript 1 representera sektionen med 6 tum och 2 representera sektionen med 8 tum får vi följande:
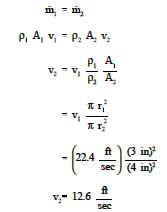
Så genom att använda kontinuitetsekvationen finner vi att ökningen av rördiametern från 6 till 8 tum orsakade en minskning av flödeshastigheten från 22.4 till 12,6 ft/sek.
Kontinuitetsekvationen kan också användas för att visa att en minskning av rördiametern orsakar en ökning av flödeshastigheten.
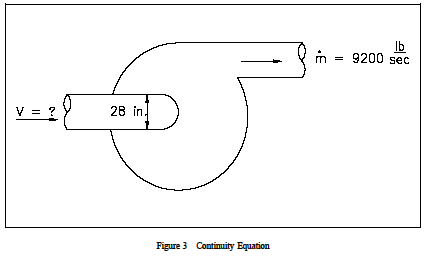
Exempel: Kontinuitetsekvationen – Centrifugalpump Inloppsdiametern för den reaktorkylmedelspump som visas i figur 3 är 28 tum medan utloppsflödet genom pumpen är 9200 lbm/sek. Vattnets densitet är 49 lbm/ft3. Vad är hastigheten vid pumpens inlopp?

Ovanstående exempel visar att flödet in i systemet är detsamma som flödet ut ur systemet. Samma koncept gäller även om mer än en flödesväg kan komma in i eller ut ur systemet samtidigt. Massbalansen justeras helt enkelt för att ange att summan av alla flöden som kommer in i systemet är lika med summan av alla flöden som lämnar systemet om stationära förhållanden råder. Ett exempel på detta fysiska fall finns i följande exempel.
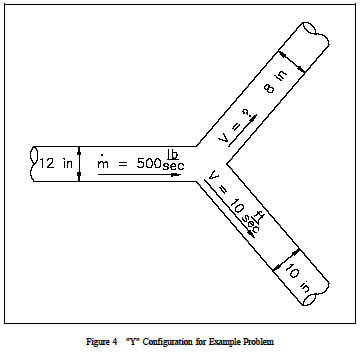
Exempel: Ett rörsystem har en Y-konfiguration för att separera flödet, vilket visas i figur 4. Inloppsbenets diameter är 12 tum och utloppsbenens diametrar är 8 och 10 tum. Hastigheten i det 10 tum långa benet är 10 ft/sek. Flödet genom huvuddelen är 500 lbm/sek. Vattnets densitet är 62,4 lbm/ft3. Vad är hastigheten ut ur den 8 tum långa rördelen?