- Konnektivitet är ett grundläggande begrepp inom grafteorin. Det definierar huruvida en graf är ansluten eller frånkopplad. Utan konnektivitet är det inte möjligt att gå igenom en graf från en topp till en annan topp.
- En graf sägs vara en konnektiv graf om det finns en väg mellan varje par toppar. Från varje hörn till varje annat hörn måste det finnas någon väg att gå. Detta kallas för en grafs konnektivitet.
- En graf sägs vara frånkopplad om det finns flera frånkopplade hörn och kanter.
- Teorier om grafens konnektivitet är viktiga i nätverkstillämpningar, routing av transportnätverk, nätverkstolerans etc.
Exempel
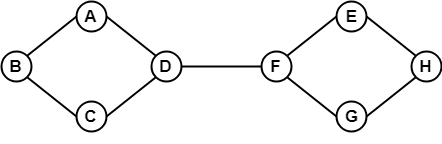
I exemplet ovan är det möjligt att resa från en hörnpunkt till en annan hörnpunkt. Här kan vi gå från punkt B till H genom att använda vägen B -> A -> D -> F -> E -> H. Det är alltså en sammanhängande graf.
Exempel
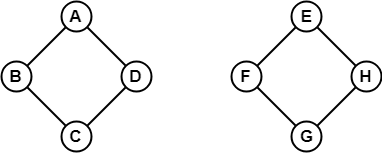
I exemplet ovan är det inte möjligt att gå från punkt B till H eftersom det inte finns någon väg mellan dem, varken direkt eller indirekt. Därför är det en okonnekterad graf.
Låt oss se några grundläggande begrepp för konnektivitet.
Cut Vertex
En enskild vertex vars avlägsnande kopplar bort en graf kallas för en cut-vertex.
Låt G vara en konnekterad graf. En vertex v i G kallas för en avklippt vertex i G, om G-v (Remove v from G) resulterar i en odelad graf.
När vi tar bort en topp från en graf kommer grafen att delas upp i två eller flera grafer. Denna topp kallas för en skuren topp.
Note: Låt G vara en graf med n toppar:
- En sammanhängande graf G kan ha högst (n-2) skårade toppar.
- Om vi tar bort en skårad topp kan en graf bli osammanhängande.
- Om en topp tas bort kan antalet komponenter i en graf öka med minst en.
- Varje icke-hängande topp i ett träd är en snittad topp.
Exempel 1

Exempel 2
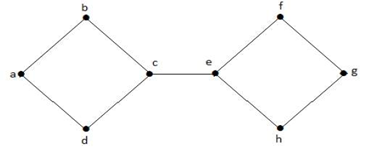
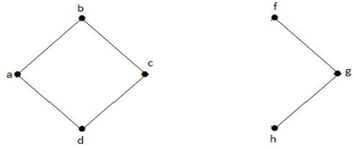
I grafen ovan är toppen ”e” en snittad topp. Efter att ha tagit bort vertex ’e’ från grafen ovan kommer grafen att bli en osammanhängande graf.
Cut Edge (Bridge)
En cut- Edge eller bridge är en enskild kant vars avlägsnande gör att en graf blir osammanhängande.
Låt G vara en sammanhängande graf. En kant e i G kallas för en avklippt kant i G, om G-e (Ta bort e från G) resulterar i en frånkopplad graf.
När vi tar bort en kant från en graf kommer grafen att delas upp i två eller flera grafer. Denna borttagna kant kallas för en skuren kant eller bro.
Note: Låt G vara en graf med n hörn:
- En sammanhängande graf G kan ha högst (n-1) skurna kanter.
- Om man tar bort en skuren kant kan en graf bli osammanhängande.
- För att ta bort en kant kan antalet komponenter i en graf öka med högst en.
- En avklippt kant ”e” får inte vara en del av någon cykel i G.
- Om det finns en avklippt kant måste det också finnas ett avklippt hörn eftersom minst ett hörn i en avklippt kant är ett avklippt hörn.
- Om det finns en avklippt topp är det inte nödvändigt att det finns någon avklippt kant.
Exempel 1
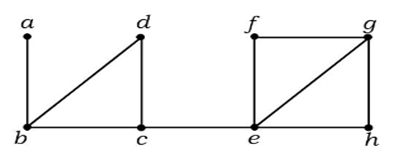
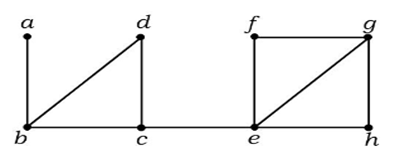
I grafen ovan är kanten (c, e) en avklippt kant. Efter att ha tagit bort denna kant från grafen ovan kommer grafen att bli en osammanhängande graf.
Exempel 2
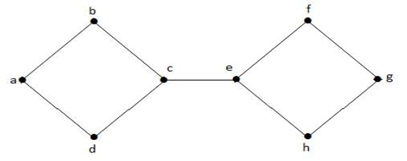
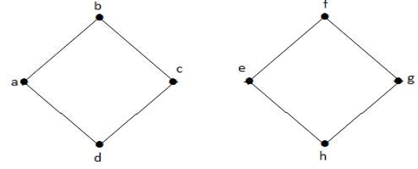
I grafen ovan är kanten (c, e) en avklippt kant. Efter att ha tagit bort denna kant från grafen ovan kommer grafen att bli en frånkopplad graf.
Snittuppsättning
I en sammanhängande graf G är en frånkopplad uppsättning en uppsättning S av kanter med följande egenskaper:
- Om alla kanter i S tas bort blir G frånkopplad.
- Om vissa kanter (men inte alla) i S tas bort, kopplas inte G från varandra.
Exempel 1
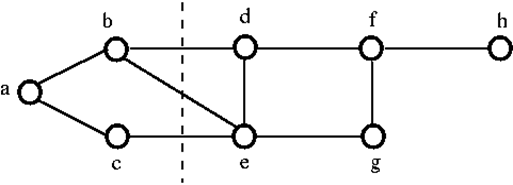
För att koppla bort grafen G ovan måste vi ta bort de tre kanterna, det vill säga bd, be och ce. Vi kan inte koppla bort den genom att bara ta bort två av de tre kanterna. Därför är {bd, be, ce} en snittmängd.
Efter att ha tagit bort snittmängden från grafen ovan skulle den se ut på följande sätt:
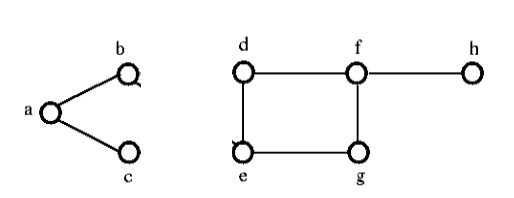
Kantkonnektivitet
Kantkonnektiviteten hos en sammanhängande graf G är det minsta antalet kanter vars avlägsnande gör G osammanhängande. Det betecknas med λ(G).
När λ(G) ≥ k sägs grafen G vara k-kantansluten.
Exempel
Låt oss se ett exempel,
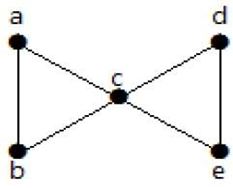
Från grafen ovan, genom att ta bort två minimikanter, blir den anslutna grafen en frånkopplad graf. Därför är dess kantkonnektivitet 2. Därför är grafen ovan en 2-kantkonnekterad graf.
Här finns följande fyra sätt att koppla bort grafen genom att ta bort två kanter:
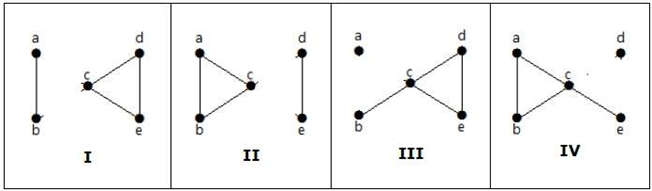
Vertexkonnektivitet
Konnektiviteten (eller vertexkonnektiviteten) hos en sammanhängande graf G är det minsta antalet hörn vars avlägsnande gör att G kopplas bort eller reduceras till en trivial graf. Den betecknas med K(G).
Grafen sägs vara k-ansluten eller k-vertexansluten när K(G) ≥ k. För att ta bort en topp måste vi också ta bort de kanter som är förbundna med den.
Exempel
Vi ska se ett exempel:
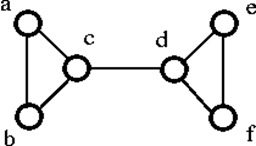
Den ovanstående grafen G kan kopplas bort genom att ta bort den enda vertexen antingen ”c” eller ”d”. Därför är dess konnektivitet 1. Därför är det en graf med 1 konnektivitet.