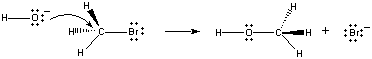Kemisk kinetik
Kemisk kinetik
Du kanske är bekant med syra-bastitreringar där fenolftalein används som slutpunktsindikator. Du kanske inte har lagt märke till vad som händer när en lösning som innehåller fenolftalein i närvaro av ett överskott av bas får stå i några minuter. Även om lösningen till en början har en rosa färg blir den gradvis färglös när fenolftaleinet reagerar med OH-jonen i en starkt basisk lösning.
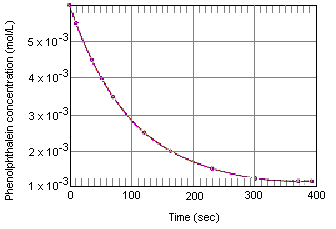
Tabellen nedan visar vad som händer med koncentrationen av fenolftalein i en lösning som till en början var 0,005 M i fenolftalein och 0,61 M i OH-jonen. Som du kan se när dessa data plottas i grafen nedan, minskar fenolftaleinkoncentrationen med en faktor 10 under en period på ungefär fyra minuter.
Experimentella data för reaktionen mellan fenolftalein och överskottsbas
Experiment som det som gav oss data i ovanstående tabell klassificeras som mätningar av kemisk kinetik (från en grekisk stam som betyder ”tomove”). Ett av målen med dessa experiment är att beskriva reaktionshastigheten den hastighet med vilken reaktanterna omvandlas till reaktionsprodukterna.
Termen hastighet används ofta för att beskriva förändringen i en kvantitet som sker per tidsenhet. Inflationshastigheten är till exempel förändringen i genomsnittskostnaden för en samling standardartiklar per år. Hastigheten med vilken ett objekt färdas genom rymden är den sträcka som tillryggaläggs per tidsenhet, t.ex. miles per timme eller kilometer per sekund. Inom kemisk kinetik är den sträcka som tillryggaläggs förändringen i koncentrationen av en av reaktionens komponenter. En reaktionshastighet är därför den förändring i koncentrationen av en av reaktanterna
(X)
som sker under en given tidsperiodt.
Praktikproblem 1:
Använd uppgifterna i tabellen ovan för att beräkna hastigheten med vilken fenolftalein reagerar med OH-jonen under var och en av följande perioder:
(a) Under det första tidsintervallet, när fenolftaleinkoncentrationen sjunker från 0,0050 M till 0,0045 M.
(b) Under det andra tidsintervallet, när koncentrationen sjunker från 0,0045 M till 0,0040 M.
(c) Under det tredje tidsintervallet, när koncentrationen sjunker från 0,0040 M till 0,0035 M.
Klicka här för att kontrollera ditt svar på övningsuppgift 1.
Klicka här för att se en lösning på övningsproblem 1.
Instant reaktionshastighet och hastighetslagen för en reaktion
Hastigheten för reaktionen mellan fenolftalein och OH-jonen är inte konstant, utan ändras med tiden. Liksom de flesta reaktioner minskar hastigheten för den här reaktionen gradvis när reaktanterna förbrukas. Detta innebär att reaktionshastigheten förändras medan den mäts.
För att minimera det fel som detta introducerar i våra mätningar verkar det tillrådligt att mäta reaktionshastigheten under tidsperioder som är korta jämfört med den tid det tar för reaktionen att inträffa. Vi kan till exempel försöka mäta den oändligt lilla förändringen av koncentrationend(X)som inträffar under en oändligt kort tidsperiod. Förhållandet mellan dessa kvantiteter kallas den momentana reaktionshastigheten.
Den momentana reaktionshastigheten vid varje tidpunkt kan beräknas från en graf över koncentrationen av reaktanten (eller produkten) i förhållande till tiden. Diagrammet nedan visar hur reaktionshastigheten för nedbrytning av fenolftalein kan beräknas från ett diagram över koncentrationen mot tiden. Reaktionshastigheten vid varje tidpunkt är lika med lutningen på en tangent som dras till denna kurva vid den tidpunkten.
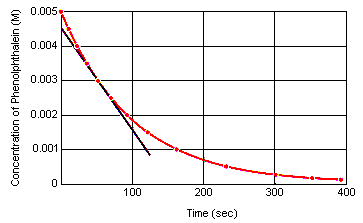
Den momentana reaktionshastigheten kan mätas vid vilken tidpunkt som helst mellan det ögonblick då reaktanterna blandas och det ögonblick då reaktionen når jämvikt.Genom att extrapolera dessa data tillbaka till det ögonblick då reagenserna blandas får man den initiala momentana reaktionshastigheten.
Rate Laws and Rate Constants
Ett intressant resultat erhålls när den momentana reaktionshastigheten beräknas vid olika punkter längs kurvan i grafen i föregående avsnitt. Reaktionshastigheten vid varje punkt på kurvan är direkt proportionell mot koncentrationen av fenolftalein vid den tidpunkten.
Rate = k(fenolftalein)
Då denna ekvation är en experimentell lag som beskriver reaktionshastigheten kallas den för reaktionens hastighetslag. Proportionalitetskonstanten, k, kallas för hastighetskonstanten.
Praktikproblem 2:
Beräkna hastighetskonstanten för reaktionen mellan fenolftalein och OH-jonen om den momentana reaktionshastigheten är 2,5 x 10-5 mol per liter per sekund när koncentrationen av fenolftalein är 0,0025 M.
Klicka här för att kontrollera ditt svar på praktikproblem 2.
Klicka här för att se en lösning på praktikproblem 2.
Praktikproblem 3:
Använd hastighetskonstanten för reaktionen mellan fenolftalein och OH-jonen för att beräkna den initiala momentana reaktionshastigheten för de experimentella data som anges i föregående tabell.
Klicka här för att kontrollera ditt svar på övningsuppgift 3.
Klicka här för att se en lösning på övningsuppgift 3.
Differenta sätt att uttrycka reaktionshastigheten
Det finns vanligtvis mer än ett sätt att mäta reaktionshastigheten för en reaktion. Vi kan till exempel studera nedbrytningen av vätejodid genom att mäta hur snabbt antingen H2 eller I2 bildas i följande reaktion eller hur snabbt HI förbrukas.
2 HI(g) H2(g) + I2(g)
Experimentellt finner vi att hastigheten med vilken I2 bildas är proportionell mot kvadraten på HI-koncentrationen vid varje tidpunkt.
Vad skulle hända om vi studerade hastigheten med vilken H2 bildas?Den balanserade ekvationen antyder att H2 och I2 måste bildas med exakt samma hastighet.
Vad skulle dock hända om vi studerade hastigheten med vilken HI förbrukas i denna reaktion? Eftersom HI förbrukas måste förändringen i dess koncentration vara ett negativt tal. Enligt konvention rapporteras hastigheten för en reaktion alltid som ett positivt tal. Vi måste därför ändra tecknet innan vi rapporterar reaktionshastigheten för en aktant som förbrukas i reaktionen.
Det negativa tecknet gör två saker. Matematiskt omvandlar det en negativ förändring i koncentrationen av HI till en positiv hastighet. Fysikaliskt påminner det oss om att reaktantens koncentration minskar med tiden.
Vad är förhållandet mellan den reaktionshastighet som erhålls genom att övervaka bildandet av H2 eller I2 och den hastighet som erhålls genom att observera hur HI försvinner? Stökiometrin för reaktionen säger att två HI-molekyler förbrukas för varje producerad H2- eller I2-molekyl. Detta innebär att HI:s nedbrytningshastighet är dubbelt så snabb som den hastighet med vilken H2 och I2 bildas. Vi kan översätta detta förhållande till en matematisk ekvation enligt följande.
Det resulterar i att den hastighetskonstant som erhålls genom att studera hastigheten med vilken H2och I2 bildas i den här reaktionen (k) inte är densamma som den hastighetskonstant som erhålls genom att övervaka hastigheten med vilken HI förbrukas (k’)
Praktikuppgift 4:
Beräkna hastigheten med vilken HI försvinner i följande reaktion i det ögonblick då I2 bildas med en hastighet på 1.8 x 10-6 mol per liter per sekund:
2 HI(g) 
H2(g) + I2(g)
Klicka här för att kontrollera ditt svar på övningsproblem 4.
Klicka här för att se en lösning på övningsproblem 4.
Hastighetslagen kontra stökiometrin för en reaktion
På 1930-talet studerade Sir Christopher Ingold och medarbetare vid University ofLondon kinetiken för substitutionsreaktioner som följande.
CH3Br(aq) + OH-(aq)
CH3OH(aq) + Br-(aq)
De fann att reaktionshastigheten för denna reaktion är proportionell mot koncentrationerna av båda reaktanterna.
Hastighet = k(CH3Br)(OH-)
När de körde en liknande reaktion på ett något annorlunda utgångsmaterial fick de liknande produkter.
(CH3)3CBr(aq) + OH-(aq) (CH3)3COH(aq) + Br-(aq)
Men nu var reaktionshastigheten proportionell mot koncentrationen av endast en av reaktanterna.
Rate = k((CH3)3CBr)
Dessa resultat illustrerar en viktig punkt: Hastighetslagen för en reaktion kan inte förutsägas utifrån reaktionens stökiometri; den måste bestämmas experimentellt. Ibland stämmer hastighetslagen överens med vad vi förväntar oss av reaktionens stökiometri.
2 HI(g) Rate = k(HI)2
Ofta, är det dock inte så.
| 2 N2O5(g) 4 NO2(g) + O2(g) |
Rate = k(N2O5) |
Molekyläritetsordning
Vissa reaktioner sker i ett enda steg. Reaktionen där en kloratatom överförs från ClNO2 till NO för att bilda NO2 och ClNO är ett bra exempel på en reaktion i ett steg.
ClNO2(g) + NO(g)
Andra reaktioner sker i en serie av enskilda steg. N2O5 sönderdelas till exempel till NO2 och O2 genom en trestegsmekanism.
Steg 1: N2O5 Steg 2: NO2 + NO3 Steg 3: NO + NO3 Stråken i en reaktion klassificeras i termer av molekyläritet, som beskriver antalet förbrukade molekyler. När en enda molekyl förbrukas kallas steget för unimolekylärt. När två molekyler förbrukas är det bimolekylärt.
Övningsuppgift 5:
Bestäm molekyläriteten för varje steg i reaktionen genom vilken N2O5 sönderdelas till NO2 och O2.
Klicka här för att kontrollera ditt svar på Övningsuppgift 5.
Klicka här för att se lösningen på Övningsuppgift 5.
Reaktioner kan också klassificeras med avseende på deras ordning. Nedbrytningen av N2O5 är en reaktion av första ordningen eftersom reaktionshastigheten beror på koncentrationen av N2O5 upphöjd till första makten.
Rate = k(N2O5)
Snedbrytningen av HI är en reaktion av andra ordningen eftersom reaktionshastigheten beror på koncentrationen av HI upphöjd till andra makten.
Rate = k(HI)2
När reaktionshastigheten för en reaktion beror på mer än en reagens, klassificerar vi reaktionen i termer av ordningen för varje reagens.
Övningsuppgift 6:
Klassificera ordningen för reaktionen mellan NO och O2 för att bilda NO2:
2 NO(g) + O2(g)
Antag följande hastighetslag för denna reaktion:
Rate = k(NO)2(O2)
Klicka här för att kontrollera ditt svar på övningsuppgift 6.
Skillnaden mellan en reaktions molekyläritet och reaktionsordning är viktig. En reaktions molekyläritet, eller ett steg i en reaktion, beskriver vad som händer på molekylär nivå. En reaktions ordning beskriver vad som händer på makroskopisk nivå. Vi bestämmer en reaktions ordning genom att se hur reaktionens produkter dyker upp eller hur reaktanterna försvinner. Reaktionens molekylära karaktär är något som vi härleder för att förklara dessa experimentella resultat.
Kollisionsteoretisk modell för kemiska reaktioner
Den kollisionsteoretiska modellen för kemiska reaktioner kan användas för att förklara de observerade hastighetslagarna för både enstegs- och flerstegsreaktioner. Modellen utgår från att hastigheten för varje steg i en reaktion beror på frekvensen av kollisioner mellan de partiklar som är involverade i det steget.
Figuren nedan ger en grund för att förstå konsekvenserna av den kollisionsteoretiska modellen för enkla reaktioner i ett steg, t.ex. följande.
ClNO2(g) + NO(g)
Den kinetiska molekylteorin antar att antalet kollisioner per sekund i en gas beror på antalet partiklar per liter. Hastigheten med vilken NO2och ClNO bildas i denna reaktion bör därför vara direkt proportionell mot koncentrationerna av både ClNO2 och NO.
Hastighet = k(ClNO2)(NO)
Kollisionsteorins modell föreslår att hastigheten för varje steg i en reaktion är proportionell mot koncentrationerna av de reagenser som förbrukas i det steget. Hastighetslagen för en reaktion i ett steg bör därför stämma överens med stökiometrin för reaktionen.
Följande reaktion sker till exempel i ett enda steg.
CH3Br(aq) + OH-(aq)
När dessa molekyler kolliderar i rätt riktning kan ett par obundna elektroner på OH-jonen doneras till kolatomen i mitten av CH3Br-molekylen, vilket visas i figuren nedan.
När detta sker bildas en kolsyrebindning samtidigt som kol-brombindningen bryts. Nettoresultatet av denna reaktion är att enOH- jon byts ut mot en Br – jon. Eftersom reaktionen sker i ett enda steg, vilket innebär kollisioner mellan de två reaktanterna, är reaktionshastigheten proportionell mot koncentrationen av båda reaktanterna.
Rate = k(CH3Br)(OH-)
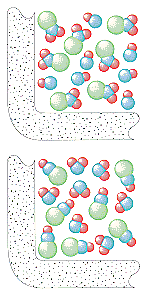
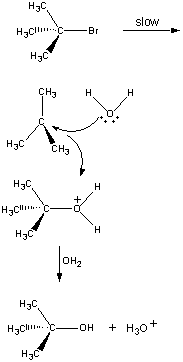
Inte alla reaktioner sker i ett enda steg. Följande reaktion sker i tre steg, enligt figuren nedan.
(CH3)3CBr(aq) + OH-(aq)
I det första steget dissocieras (CH3)3CBr-molekylen till ett jonpar.
Första steget Den positivt laddade (CH3)3C+-jonen reagerar sedan med vatten i ett andra steg.
Det andra steget Produkten av denna reaktion förlorar sedan en proton till antingen OH-jonen eller vatten i det sista steget.
Tredje steget Det andra och tredje steget i den här reaktionen är väldigt mycket snabbare än det första.
(CH3)3CBr Långsamt steg (CH3)3C+ + H2O Snabbt steg (CH3)3COH2+ + OH- Snabbt steg Den totala reaktionshastigheten är därför mer eller mindre lika med hastigheten i det första steget. Det första steget kallas därför det hastighetsbegränsande steget i denna reaktion eftersom det bokstavligen begränsar den hastighet med vilken reaktionens produkter kan bildas. Eftersom endast en reagens är inblandad i det hastighetsbegränsande steget är den totala reaktionshastigheten proportionell mot koncentrationen av endast denna reagens.
Rate = k((CH3)3CBr)
Hastighetslagen för denna reaktion skiljer sig därför från vad vi skulle förutsäga utifrån reaktionens stökiometri. Även om reaktionen förbrukar både (CH3)3CBrand OH- är reaktionshastigheten endast proportionell mot koncentrationen av(CH3)3CBr.
Hastighetslagarna för kemiska reaktioner kan förklaras med följande allmänna regler.
Hastigheten för varje steg i en reaktion är direkt proportionell mot koncentrationerna av de reagenser som förbrukas i det steget.
Den totala hastighetslagen för en reaktion bestäms av sekvensen av steg, eller mekanismen, genom vilken reaktanterna omvandlas till reaktionens produkter.
Den totala hastighetslagen för en reaktion domineras av hastighetslagen för det långsammaste steget i reaktionen.
