Hur många sidor har en cirkel?

Det är en läxfråga från grundskolan som orsakar oenighet bland erfarna matematiker. För att hitta det rätta svaret använde jag mig av det mest rigorösa av vetenskapliga instrument, Twitter-undersökningen:

I efterhand ångrar jag att jag inte inkluderade ett ”inget av ovanstående”-alternativ, men mer om det senare. I det här inlägget kommer jag att gå igenom dessa tre svar (och ”inget av ovanstående”) och diskutera deras för- och nackdelar som jag ser dem, innan jag dramatiskt avslöjar det korrekta svaret.

Men först: varför kan vi inte rakt av ge det rätta svaret? Orden i frågan är knappast mystiska. Vi vet alla vad en ”cirkel” är, vad det innebär att räkna ”hur många” av något och vad en ”sida” är… eller hur? Här är (grova) definitioner som jag har fått fram genom diskussioner med två grundskoleelever som har fått den här frågan:

1. En linje som utgör en del av en forms gräns för en plan figur.

Syftet med att säga plan figur snarare än ”form” här är att vi vill ha former som lever i två dimensioner (t.ex. kvadrater eller cirklar, men inte sfärer eller kuber). Nästa fråga är vad en ”linje” är i definition 1. Här är en variant som fastställer det:

2. En rak linje som utgör en del av gränsen för en plan figur.

Om du skriver ”define: side” i Google är den mest relevanta definitionen:

En rätlinig figur är en figur som är uppbyggd av raka linjer. Denna definition är alltså en ytterligare förfining av definition 2 och gör det möjligt för oss att hävda att en kvadrat har fyra sidor, men den har på ytan inget att säga om icke rätlinjiga plana figurer som cirklar.

Infinitely Many Sides?

Jag tror att det är en säker gissning att de som svarat på min Twitter-omröstning har en högre nivå av matematisk utbildning än det nationella genomsnittet. Det faktum att de var splittrade på den här frågan överhuvudtaget, och att en liten majoritet valde ett svar som den vanliga målgruppen för den här frågan (grundskoleelever) inte har tillgång till, tyder verkligen på att det är något som är fel någonstans.

Så, har en cirkel oändligt många sidor? Det är definitivt användbart att betrakta en cirkel som gränsen för polygoner med n sidor när n blir större och större. Detta är exakt det tillvägagångssätt som Archimedes, Liu Hui och otaliga andra har använt genom århundradena för att studera cirkulär geometri, inklusive att komma fram till approximationer för π.

En utgåva från 1500-talets Ming-dynastin av Jiuzhang suanshu (Nine Chapters on the Mathematical Art), tredje århundradet e.Kr.

Ibland är det absolut förnuftigt, som en bekväm förkortning, att tänka sig att en cirkel är som en polygon med oändligt många sidor.

Men som en outhärdlig pedant en matematiker skulle jag vilja skilja mellan bekväm förkortning och bokstavlig sanning. Om vi håller fast vid att en cirkel verkligen är en polygon med oändligt många sidor, så inställer sig frågan: Vilka är sidorna? Och det enda rimliga svaret är säkert: de enskilda punkterna i cirkeln. Hur långa är dessa så kallade sidor? Noll centimeter. Och är dessa sidor åtskilda av hörn? Uppenbarligen inte, antingen finns det inga hörn alls, eller så är varje punkt både en sida och ett hörn.

Jag skulle säga att sidor med längden noll är … ett problematiskt begrepp. Hur kan man veta om man har några? Anta till exempel att jag studerar ett system där en kvadrat uppstår som en gräns för oktagoner så här:

I den här situationen kan det mycket väl vara vettigt för mig att tänka mig att min kvadrat har åtta sidor, varav fyra har längden noll. Men om jag skulle insistera på att min (helt vanliga) kvadrat verkligen har åtta sidor, skulle du kanske höja ett ögonbryn.

Så detta – det vinnande svaret i min omröstning – är det enda som jag kommer att förklara vara definitivt fel, samtidigt som det är det enda som ger någon geometrisk insikt överhuvudtaget. En paradox? Inte riktigt. Att resonera genom analogier är en värdefull färdighet i matematik och i livet; samtidigt är det viktigt att hålla fast vid insikten om att det är vad vi gör.

För oändligt många sidor: geometriskt belysande.
Mot oändligt många sidor: åttasidiga kvadrater.

Off on a tangent 1: apeirogoner

Även om en cirkel inte är en cirkel, finns det då sådana saker som polygoner med oändligt många sidor? Tja, det finns ett ord för att beskriva en sådan sak en apeirogon. En regelbunden apeirogon skulle då ha sidor av samma (icke-noll) längd med lika stora vinklar mellan dem. Det enda alternativet här är detta förbluffande ointressanta objekt:

Om du har invändningar mot att detta är en ”polygon” (antingen på grund av vinklarna på 180° eller för att kedjan av kanter inte slutar i en slinga), vad sägs om något som liknar detta: Börja i botten av en cirkel och förflytta dig vid varje tillfälle runt hälften av det som återstår av cirkeln, och ersätt den båge du just har färdats med en rak linje:

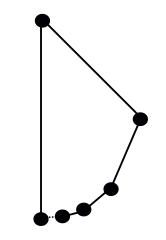
Är detta en äkta polygon? Återigen beror det på dina termer. Enligt en vanlig definition, den av en ”sluten polygonal kedja”, uppfyller detta inte kraven eftersom starthörnet (längst ner till vänster) endast ansluter till en kant. Men det är mycket nära att misslyckas: den punkten är gränsen för en sekvens av kanter från höger, vilket gör den här formen till en ”icke-självskärande styckevis linjär sluten kurva”, en annan definition av polygon som folk använder.

Om vi lämnar vår vanliga euklidiska värld och ger oss in i det hyperboliska rummet, så finns det ingen tvetydighet. Apeirogoner (även regelbundna apeirogoner) existerar helt enkelt:

En kakelkonstruktion av det hyperboliska planet med regelbundna apeirogoner. (Av Anton Sherwood – Eget arbete, Public Domain, https://commons.wikimedia.org/w/index.php?curid=13260274 )

Off on a tangent 2: extreme points

Det kan vara mer försvarbart att säga att en cirkel har oändligt många hörn än oändligt många sidor (även om detta inte är en fråga som verkar ställas särskilt ofta). Till att börja med, om ett hörn på en kvadrat är en punkt där dess begränsningslinje inte är rak, så uppfyller varje punkt på cirkeln detta. Mer sofistikerat finns det ett begrepp om en extrem punkt i en form: det är varje punkt genom vilken man kan dra ett segment av en rak linje som berör formen endast i just den punkten. För en kvadrat och många välkända former sammanfaller ytterpunkterna exakt med hörnen. Varje punkt på cirkelns gräns är en extrempunkt, så det är säkert sant att en cirkel har oändligt många.

Vi kan oroa oss för att vissa former, som den här chevronen, har hörn som inte är extrempunkter:

Här är det nedre centrala hörnet inte en extrempunkt (de andra tre hörnen är det). Det som är fel är att den här formen inte är konvex (i grova drag har den några bitar som sticker ut för långt). En cirkel är konvex, så vi behöver kanske inte oroa oss. Alternativt skulle vi kunna råda bot på situationen genom att definiera ett ”hörn” som en punkt som är en extrem punkt antingen i formen i fråga eller i dess komplement, dvs. hela planet med formen utskuren ur det. På så sätt skulle man kunna upptäcka hörn på alla polygoner, inklusive chevron. För släta kurvor skulle den identifiera alla gränspunkter som ”hörn” med undantag för böjningspunkter (vilket inte är orimligt eftersom vi skulle kunna hävda att gränsen är rak där).

En sida?

I grundskolan verkar det som om ”en” är det svar som får ett kryss. Och det finns en någorlunda hygglig motivering. Kom ihåg definition 1 ovan:

1. En linje som utgör en del av gränsen för en plan figur.

Den omedelbara frågan är vad som räknas som en ”linje”, särskilt om vi inte insisterar på rakhet. Om vi är alltför avslappnade när det gäller detta kan varje plan figur sägas ha ”en sida”, i samma bemärkelse som den har en avgränsning, perimeter eller omkrets. Men detta måste vara fel, eftersom vi säkert vill att en kvadrat ska ha fyra sidor. En kvadrat har fyra punkter där den inte är jämn, med fyra jämna partier däremellan. Kanske var det verkligen de släta delarna som vi räknade hela tiden. Så underförstått har vi en ny förfining av definition 1 (och tar också tillfället i akt att slopa den vaga termen ”figur”):

4. Varje slät sektion av en styckevis slät sluten kurva.

En ”sluten kurva” är en kurva som går i en slinga för att möta sig själv, så att den inte har några fria ändar. ”Styckvis slät” innebär att den är uppbyggd av släta delar som möts i isolerade oregelbundna punkter. Det är helt legitimt att vilja räkna de släta sektionerna av en sådan forms gräns, och det är inte alls upprörande att använda ordet ”sida” när man gör det. Så jag säger verkligen inte att detta definitivt är fel svar.

Frågan är om denna tolkning av ”sida” inte bara är sammanhängande, utan tillräckligt naturlig för att den helt enkelt kan förutsättas utan att uttryckligen anges (vilket den sällan eller aldrig gör). Vad händer när jämnhet och rakhet stämmer olika? Betrakta denna gravstensform, skapad genom att ersätta toppen av en kvadrat med en halvcirkel med samma diameter.

Denna har två släta delar (den nedre linjen och resten) men tre raka kanter (plus ett böjt stycke som smidigt sammanfogar två av dem). Hur många sidor har den då? Jag rådfrågade mina Twitter-vänner igen:

Den här gången borde jag ha inkluderat ”oändligt många” som ett alternativ, även om det kan absorberas i ”Inget av ovanstående”. Den som röstar på att cirkeln har oändligt många sidor bör automatiskt rösta ”Ingen av ovanstående” här, såvida inte – vilket är ett viktigt förbehåll – den här formens natur ger läsaren en annan uppfattning om ”sida”. Det faktum att de mest populära valen i dessa två omröstningar är oförenliga tyder på att detta kan vara fallet (eller förstärker åtminstone att vattnen är grumliga).

Och även om två är ett fullt respektabelt svar, som är förenligt med definition 4 ovan och med en cirkels ensidighet, är jag inte övertygad om att det definitivt är det rätta svaret, eller att tre eller fyra är kategoriskt fel. Det beror på vad man vill räkna: släta sektioner, raka kanter eller raka kanter plus det som blir över, vilket kan vara det svar man vill ha beroende på sammanhanget (mer om detta nedan). I samband med detta är jag inte säker på att räkna antalet släta sektioner helt och hållet överensstämmer med min intuition av ordet ”sida”. När allt kommer omkring är gravstenens två upprättstående sektioner – jag tror att det är rättvist att säga – ”på motsatta sidor”. Är vi verkligen nöjda med att de samtidigt är en del av ”samma sida”?

Du kanske protesterar mot att jag blandar ihop två olika betydelser av ”sida”, att terminologin ibland krockar och att vi bara måste leva med det. Jag är dock inte så säker på det. Poängen med den här övningen är att extrapolera från en situation (rätlinjiga figurer) där de två begreppen passar ganska bra ihop. Om det fanns en ny idé som innefattade allt som vi gillade med originalet, men som också tillämpades på en bredare kategori av figurer, skulle den ha ett överväldigande anspråk på att vara det enda rätta svaret. Men om alla våra försök till generalisering innebär att vi offrar önskvärda aspekter av originalet, finns det kanske ingen enda korrekt generalisering. Det finns olika alternativ, med olika kompromisser, som kan vara lämpliga i olika sammanhang (och om vi befinner oss i en situation där mer än ett alternativ är aktuellt, kan de med fördel ges olika namn).

Här är en annan variant: en Weierstrass-gravsten som skapas genom att ersätta den övre kanten av en kvadrat med ett avsnitt av Weiestress-funktionen, en oändligt vickande linje som inte är slät någonstans.

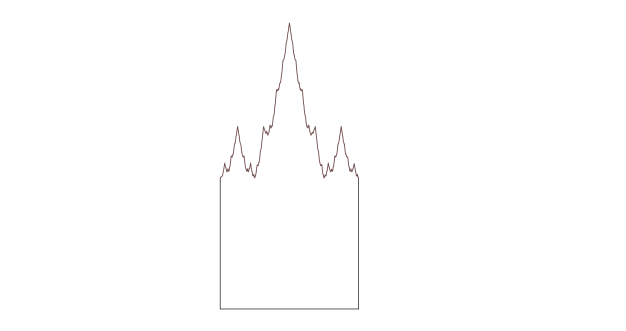
Här (och upptäck stavfelet) är vad mina Twitter-vänner tyckte om detta – även om färre vågade sig på en åsikt:

Trots skepticismen hos mina Twitter-följare ska jag strax förklara varför jag inte tycker att det är fånigt att se det som att den här har fyra sidor (varav en inte är slät). Å andra sidan, om du föredrar släta sidor har du återigen ett val mellan att se det som att den har oändligt många sidor (varav tre har längden 1 och resten har längden 0), eller att den har tre sidor plus en sträcka med en gräns som definitivt inte är en sida.

För en sida: en enda slät kurva.
Mot en sida: samma sida på motsatta sidor.

Off on a tangent 3: sidor kontra kanter

Hur många sidor har en kvadrat? Fyra. Hur många kanter har den? Fyra. Är kanter och sidor då samma sak? Inte nödvändigtvis. Här är två konfigurationer som är – åtminstone enligt argumentationen – var och en fyrsidig men som har 5 respektive 3 kanter:

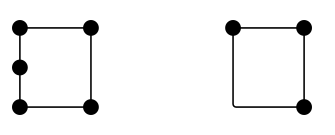
Som regel skulle jag säga att en ”kant” är ett topologiskt objekt, i det att det är dess funktion, inte dess form, som är det viktiga. Tänk på kartan över Londons tunnelbana. Om man frågar hur många kanter det finns i det nätet finns det ingen poäng i att räkna upp raka eller släta sträckor. Det är förbindelserna mellan stationer (eller hörn) som räknas.

Som redan nämnts är det vanligt att tänka på en polygon som ett mycket enkelt slags nätverk som kallas en sluten polygonal kedja: en rad hörn (i det här fallet polygonens hörn), som är sammanlänkade med kanter på ett sådant sätt att varje hörn ligger på exakt två kanter, och det hela bildar en enda slinga. I denna situation sammanfaller kanter och sidor, liksom hörn och hörn. Men i allmänhet kan man bryta denna samstämmighet, som i de två små nätverken ovan.

Om man vill tänka på saker och ting nätverksteoretiskt, men hörnen inte är tydligt markerade, måste man gissa var de finns. Med en polygon är detta lätt – hörnen finns i hörnen – vilket är anledningen till att det är så naturligt att växla mellan geometriska och topologiska tillvägagångssätt. Men med andra former, t.ex. någon av gravstenarna ovan, är det kanske inte lika självklart. Om du skulle få höra att det finns hörn någonstans där inne och om du skulle få i uppdrag att lokalisera dem, tror jag att det skulle vara klokt att gissa att det finns fyra hörn, nämligen hörnen på den ursprungliga kvadraten, och att den översta kanten av någon anledning har representerats som en icke rak linje. Och om vi vill tänka på saker och ting på det sättet, att var och en av gravstenarna har fyra kanter, kan det tyckas vara peverse (även om det är logiskt sammanhängande!).) för att insistera på att de har ett annat antal sidor (särskilt eftersom den övre sidan – trots sin egen geometri – tydligt är ”på en sida” av figuren). I stället för att gissa frågade en av mina Twitter-korrespondenter mig faktiskt: ”Har båda de övre hörnen tagits bort?”, en fråga som bara är meningsfull ur ett nätverksteoretiskt perspektiv.

Var lämnar detta cirkeln? Problemet är att ingen punkt på cirkeln har ett bättre anspråk på att vara topp än någon annan. Så även om det är frestande (och återigen logiskt) att betrakta en cirkel som ett nätverk med en kant, finns det ingen uppenbar anledning att föredra en punkt framför något annat antal om vi ska lägga in hörn.

Kan vi betrakta den som ett nätverk utan några hörn alls, ett slags tunnelbanelinje utan stationer? Den vanliga matematiska uppfattningen av ett nätverk skulle inte tillåta detta, men det borde inte avskräcka oss alltför mycket. Detta tyder på ett rent topologiskt tillvägagångssätt. Problemet är att ur den synvinkeln kan en cirkel visserligen vara ett slags nätverk utan hörn och med en kant, men det är en kvadrat också (om det är så som tunnelbanelinjen råkar vara utformad). Inom topologin är en kvadrat en cirkel. (Detta är ingen paradox, utan innebär helt enkelt att gränsen är en enda slinga vars form inte spelar någon roll). Så även om den här sortens nätverk har ”en kant” har en kvadrat uppenbarligen inte ”en sida”, så förhållandet mellan sidor (geometriska) och kanter (topologiska) har återigen brutits upp, precis som i de två små nätverken på bilden ovan. Detta tillvägagångssätt leder oss alltså inte särskilt långt.

Inga sidor?

Det kan tyckas paradoxalt att hävda att en cirkel (eller vilken form som helst) inte har ”några sidor”. Men argumentet för försvaret är enkelt. Vi återgår till definition 2:

2. En rak linje som utgör en del av gränsen för en plan figur.

Detta är en enkel, lättförståelig fras som perfekt fångar sidorna på en kvadrat. Vi har inte lyckats hitta en tillfredsställande generalisering av detta till krökta figurer, så det bästa är att hålla sig till originalet. Och en cirkel har inga.

För inga sidor: sant, enligt ett förnuftigt begrepp om ”sida”.
Mot inga sidor: låter som en Zen-koan.

Ingen av ovanstående?

Har du en definition från Google:

3. Var och en av de linjer som utgör gränsen för en plan rätlinjig figur.

Varje försök att tillämpa detta på en cirkel – en icke-rätlinjig figur – ger ingenting. Frågan är lika meningslös som ”Hur många sidor har måndagen?”

Då definition 3 är den mest officiella (den enda i det här inlägget som inte är påhittad av mig eller mina barn), gör inte det att ”Ingen av ovanstående” kategoriskt är det rätta svaret? Kanske. Å andra sidan: När någon ställer en fråga till oss kräver kanske principen om välgörenhet att vi antar att den är meningsfull om vi inte kan fastställa något annat, och definitionerna 1, 2, 4 och andra varianter gör det möjligt. Vidare är definition 3 språklig snarare än formellt matematisk, och är därför deskriptiv snarare än normativ, så vi bör inte vara förskräckta av den.

För inget av ovanstående: semantiskt fel.
Mot inget av ovanstående: dialogisk välgörenhet.

Det rätta svaret

Vad fick mig att skriva det här inlägget? Liksom otaliga grundskoleelever fick mina femåriga tvillingsöner – de grundskoleelever som nämndes i början – nyligen den här frågan i sin läxa. Den ena valde ”1” och den andra ”0”, och jag har försökt fånga och utveckla deras resonemang ovan. Jag tycker att båda svaren är fullt försvarbara – och inget av dem är definitivt rätt.

Så, vad ska du göra om du får frågan: Hur många sidor har en cirkel? Enligt min åsikt är det optimala svaret att be matematikern i ditt liv att skriva en 3000 ord lång avhandling om ämnet, som du sedan kan skriva ut och triumferande överlämna till din olyckliga lärare. Men om det inte är möjligt är det bästa tillvägagångssättet att följa Sokrates exempel och besvara frågan med en motfråga: Vad menar du med ”sida”?

När allt är sagt och gjort säger det att räkna upp till noll, eller till ett, eller att vägra svara på frågan, oss praktiskt taget ingenting om cirkels geometri. Men det finns mycket att vinna på att plocka isär välkända begrepp, släppa eller lägga till extra villkor, utmana vår intuition genom att gå från ett sammanhang till ett något annorlunda sammanhang och försöka skriva ner exakt vad vi menar med en viss term i en viss miljö. Det är vad riktig matematik handlar om.

Fotnoter

Man skulle kunna göra något annat: t.ex. välja en startpunkt P på cirkeln, från vilken man mäter avståndet runt omkretsen. Sedan förklarar man att de punkter som ligger på ett rationellt avstånd från P är hörn och resten är sidor. Detta leder till ett oräkneligt oändligt antal hörn och ett oräkneligt oändligt antal sidor. Eller så skulle man kunna fastställa motsatsen. Detta skulle kunna passa bra för polygonalgränsmetoden för cirklar, men jag skulle ha svårt att hålla med om att det är enkelt eller uppenbart nog för att betraktas som ”det rätta svaret”.

En av mina Twitter-korrespondenter oroade sig för hur jämn kurvan är. Denna gravsten är kontinuerligt differentierbar men inte dubbelt så. Det skulle säkert vara intressant om många tyckte att detta var en kritisk fråga, och detta skulle förmodligen kunna testas med en oändligt slät gravsten byggd av något liknande, även om jag inte har tänkt igenom detaljerna.

Vi skulle kunna försöka formalisera detta på följande sätt: I en kvadrat (eller vilken polygon som helst) har en sida den egenskapen att man, med utgångspunkt från vilken position som helst i insidan, kan skära formen rakt genom sin plats, så att den valda sidan ligger stadigt på en sida av snittet. Detta fungerar inte för den tvåsidiga gravstenen: varje snitt kommer alltid att skära av den långa sidan. Vi skulle kunna försvaga detta genom att säga att för att räknas som en sida måste det finnas minst ett sätt att skära igenom formen så att sidan ligger på en sida av snittet. Det skulle göra det möjligt för oss att säga att gravstenen har fyra sidor (även om den böjda delen inte ligger på en sida av punkterna i det övre området). När det gäller cirkeln är dess förmodade ena sida dock aldrig på en sida (vilket skulle uteslutas), och endast den raka delen av en halvcirkel skulle räknas som en sida.

Det är inte lätt att komma på en rigorös motivering som fungerar för båda gravstenarna, men jag tänker mer informellt i termer av Schellingpunkter: det vill säga platser som sticker ut som speciella av skäl som kanske inte är lätta att förutsäga i förväg.

Acknowledgements

Tack till alla som deltog i eller retweetade mina omröstningar, eller diskuterade detta med mig på Twitter.