GeeksforGeeks

Förutsättning – Grunderna i grafteori – uppsättning 1
En graf är en struktur som består av en uppsättning objekt där vissa par av objekten på något sätt är ”relaterade”. Objekten i grafen motsvarar hörn och relationerna mellan dem motsvarar kanter. En graf avbildas schematiskt som en uppsättning punkter som avbildar hörn som är förbundna med linjer eller kurvor som avbildar kanter.
Formellt,

”En graf består av , en icke-tom mängd hörn (eller noder) och , en mängd kanter. Varje kant har antingen en eller två hörn associerade med den, som kallas dess ändpunkter.”

Typer av grafer :Det finns flera typer av grafer som skiljer sig åt på grundval av kanter, deras riktning, deras vikt etc.

1. Enkel graf – En graf där varje kant förbinder två olika hörn och där inga två kanter förbinder samma par hörn kallas en enkel graf. Tänk till exempel på följande graf –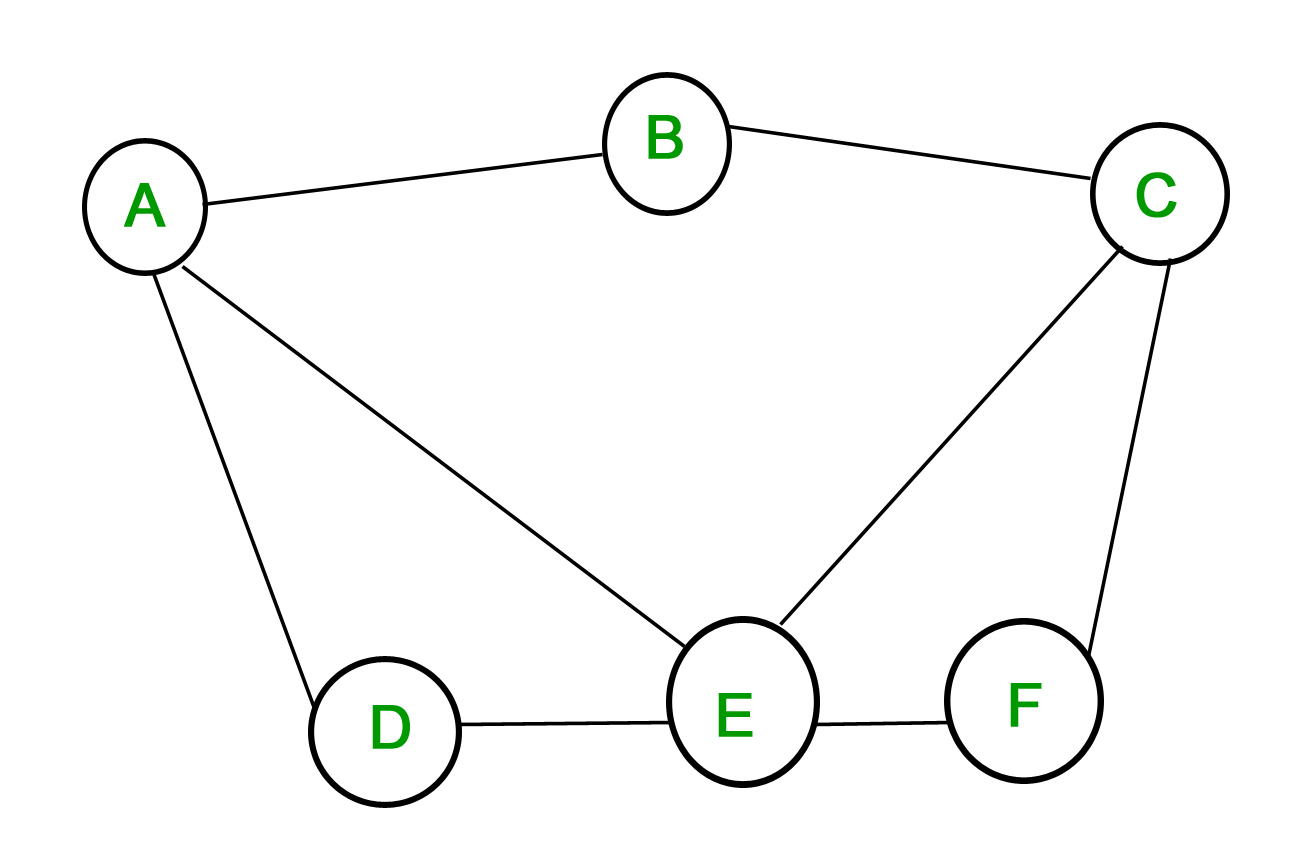

Ovanstående graf är en enkel graf, eftersom ingen hörnpunkt har en egen slinga och inga två hörnpunkter har mer än en kant som förbinder dem.
Kanterna betecknas med de hörnpunkter som de förbinder- är den kant som förbinder hörnpunkterna och .

2. Multigraph – En graf där flera kanter kan förbinda samma par av hörn kallas multigraph.
Då det kan finnas flera kanter mellan samma par av hörn, säger mångfalden av kanter hur många kanter som finns mellan två hörn.

Den ovanstående grafen är en multigraph eftersom det finns flera kanter mellan och . Multiplikatorn för kanten är 2.

I vissa grafer, till skillnad från de som visas ovan, är kanterna riktade. Detta innebär att relationen mellan objekten endast är enkelriktad och inte dubbelriktad. Kantens riktning kan vara viktig i vissa tillämpningar.

Baserat på om kanterna är riktade eller inte kan vi ha riktade grafer och oriktade grafer. Denna egenskap kan utvidgas till enkla grafer och multigrafer för att få enkla riktade eller oriktade enkla grafer och riktade eller oriktade multigrafer.

Grundläggande grafterminologi :

I diskussionen ovan har vissa termer om grafer redan förklarats, t.ex. hörn, kanter, riktade och oriktade kanter osv. Det finns fler termer som beskriver egenskaper hos hörn och kanter.

• Närhet – I en graf sägs två hörn och vara angränsande om de är ändpunkter för en kant. Kanten sägs vara intill hörnpunkterna.
  Om kanten är riktad sägs vara angränsande till och sägs vara angränsande till . Här sägs vara den inledande toppen och sägs vara den avslutande toppen.
• Grad – Graden av en topp är antalet kanter som är inkommande med den, med undantag för den egna slingan som bidrar dubbelt till toppens grad. Graden av en topp betecknas som .
  För riktade grafer klassificeras graden vidare som in-degree och out-degree. En topps ingrad är antalet kanter med den givna toppen som slutpunkt. En topps out-degree är antalet kanter med den givna toppen som utgångspunkt. In-degree betecknas som och out-degree betecknas som .
  Till exempel i den riktade grafen som visas ovan och som beskriver flygningar mellan städer, är in-degree för vertexen ”Delhi” 3 och dess out-degree är också 3.

Anm.: Om en vertex har noll grad, kallas den isolerad. Om graden är ett kallas den hängande.

Handslagssats :

Vad skulle man få om graderna för alla hörn i en graf adderas. När det gäller en odirigerad graf bidrar varje kant två gånger, en gång för sin initiala vertex och en andra gång för sin terminala vertex. Så summan av graderna är lika med dubbelt så många kanter. Detta faktum anges i handshaking-satsen.

Let  be an undirected graph with  edges. ThenIn case G is a directed graph,

Handshaking-satsen, för odirigerade grafer, har ett intressant resultat –

An undirected graph has an even number of vertices of odd degree.

Bevis : Låt och vara uppsättningar av hörn med jämna respektive udda grader.
Vi vet genom handskakningssatsen att,

Så,

Summan av graderna för hörn med jämna grader är jämn. LHS är också jämn, vilket innebär att summan av grader för hörn med udda grader måste vara jämn.
Därmed är antalet hörn med udda grader jämnt.

Några speciella enkla grafer :

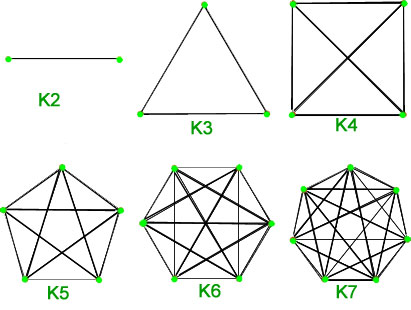
1. Kompletta grafer – En enkel graf med hörn som har exakt en kant mellan varje hörnpar kallas en komplett graf. En fullständig graf med hörn betecknas med . Det totala antalet kanter är n*(n-1)/2 med n hörn i en komplett graf.

2. Cyklar – Cyklar är enkla grafer med hörn och kanter . En cykel med hörn betecknas som . Det totala antalet kanter är n med n hörn i cykelgrafen.

3. Hjul – Ett hjul är precis som en cykel, med ytterligare ett hörn som är kopplat till alla andra hörn. Hjul med hörn med 1 extra hörn betecknas med . Det totala antalet kanter är 2*(n-1) med n hörn i hjulgrafen.

4. Hyperkuben – Hyperkuben eller n-kuben är en graf med hörn som var och en representeras av en sträng med n bitar. De hörn som skiljer sig åt med högst 1 bit är sammankopplade med kanter. En hyperkub med hörn betecknas med . Det totala antalet kanter är n* med hörn i kubgrafen.

5. Tvådelade grafer – En enkel graf sägs vara tvådelad om dess toppuppsättning kan delas upp i två disjunkta uppsättningar så att varje kant i har sin begynnelsepunkt i den första uppsättningen och slutpunkten i den andra uppsättningen. Det totala antalet kanter är (n*m) med (n+m) hörn i en tvådelad graf.

Sats – En enkel graf är tvådelad om och endast om det är möjligt att tilldela en av två
olika färger till varje hörn i grafen så att inga två intilliggande hörn tilldelas samma
färg.

En tvådelad graf med och hörn i sina två disjoktanta delmängder sägs vara komplett om det finns en kant från varje hörn i den första uppsättningen till varje hörn i den andra uppsättningen, för totalt kanter. En fullständig tvådelad graf med hörn i den första uppsättningen och hörn i den andra uppsättningen betecknas som .

GATE CS Corner Questions

Om du vill testa dina kunskaper kan du öva på följande frågor. Alla frågor har ställts i GATE under tidigare år eller i GATE Mock Tests. Det rekommenderas starkt att du övar dem.

1. GATE CS 2013, fråga 25
2. GATE CS 2014 Set-1, fråga 61
3. GATE CS 2006, fråga 71
4. GATE CS 2002, fråga 25
5. GATE CS 2004, fråga 37
6. GATE CS 2014 Set-2, fråga 13

Referenser-

Graphs – Wikipedia
Discrete Mathematics and its Applications, av Kenneth H Rosen

Denna artikel har bidragits av Chirag Manwani. Om du gillar GeeksforGeeks och vill bidra kan du också skriva en artikel via contribute.geeksforgeeks.org eller maila din artikel till [email protected]. Se din artikel dyka upp på GeeksforGeeks huvudsida och hjälp andra Geeks.